A tunnel is dug across the earth of mass 'M' and radius 'R' at a distance $R / 2$ from the centre 'O' of the Earth as shown. A body is released from rest from one end of the smooth tunnel. The velocity acquired by the body when it reaches the centre 'C' of the tunnel is

A

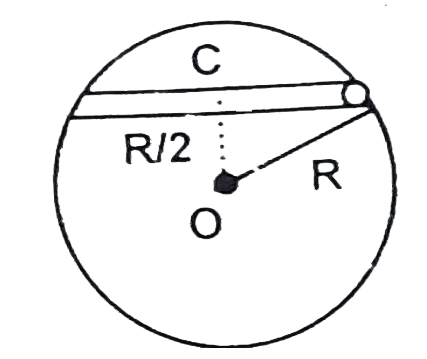
$\sqrt{\frac{3 G M}{2 R}}$

B

$\sqrt{\frac{3 G M}{4 R}}$

C

$\sqrt{\frac{3 G M}{8 R}}$

D

$d \sqrt{\frac{3 G M}{16 R}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Using conservation of energy
$\frac{1}{2} m v^{2} = - \frac{G M m}{R} - (\frac{- 11 G M m}{8 R})$
$\frac{1}{2} m v^{2} = \frac{3 G M n}{8 R}$
$∴ V = \sqrt{\frac{3 G M}{4 R}}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
A tunnel is dug along a chord of the earth at a perpendicular distance $R / 2$ from the earth's centre. The wall of the tunnel may be assumed to be frictionless. A particle is released from one end of the tunnel. The pressing force by the particle on the wall, and the acceleration of the particle vary with $x$ (distance of the particle from the centre) according to
A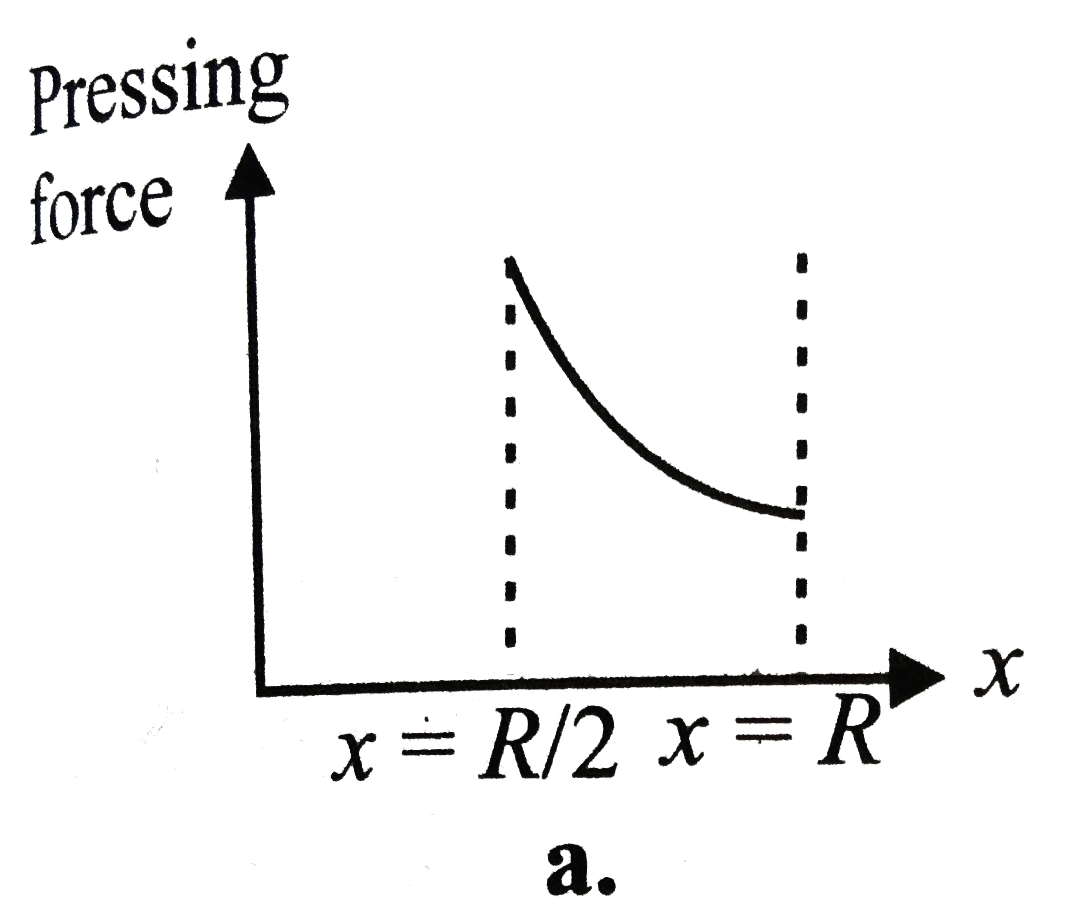
B
C
D
Question 2 - Select One
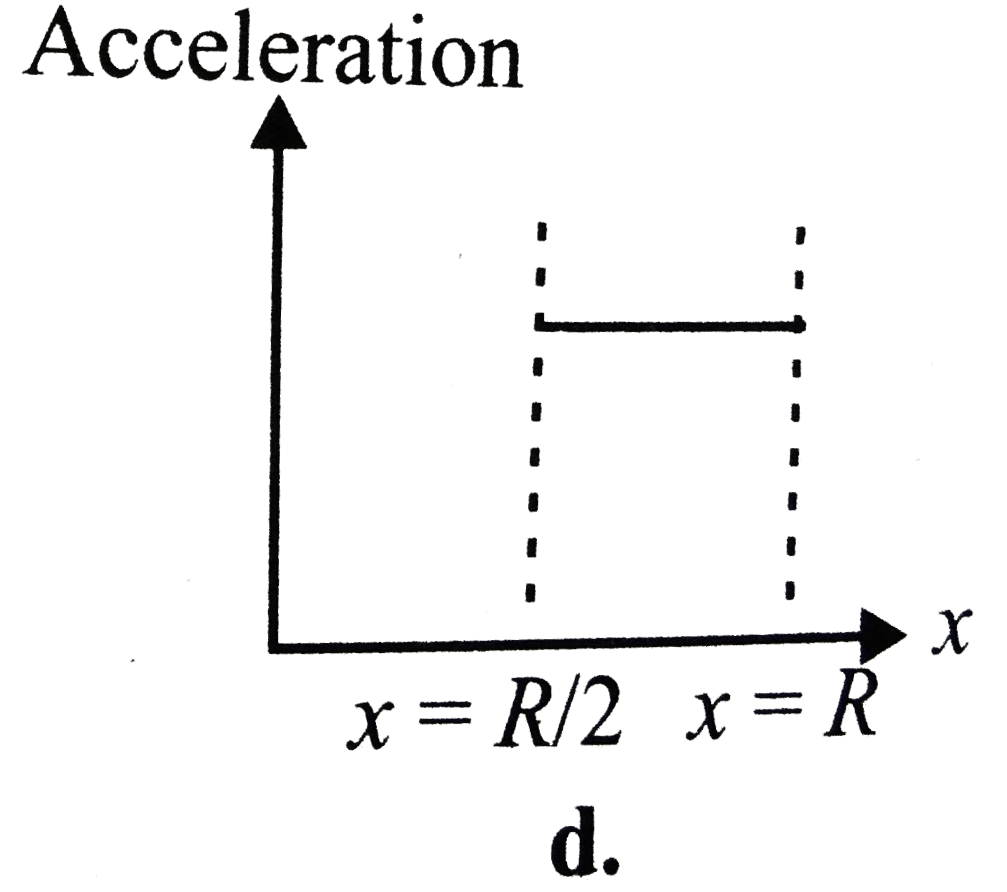
A tunnel has been dug through the centre of the earth and a ball is released in it. It will reach the other end of the tunnel after
A84.6 min
B42.3 min
C1 day
DWill not reach the other end
Question 3 - Select One
A body starts from rest from a point distant $r_{0}$ from the centre of the earth. It reaches the surface of the earth whose radius is $R$ . The velocity acquired by the body is
A $2 G M \sqrt{\frac{1}{R} - \frac{1}{r_{0}}}$
B $\sqrt{2 G M (\frac{1}{R} - \frac{1}{r_{0}})}$
C $G M \sqrt{\frac{1}{R} - \frac{1}{r_{0}}}$
D $\sqrt{G M (\frac{1}{R} - \frac{1}{R_{0}})}$

FIITJEE-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile