A body released at the distance r(r>R) from the centre of the earth. What is the velocity of the body when it strikes the surface of the earth?
To find the velocity of a body when it strikes the surface of the Earth after being released from a distance r (where r>R, with R being the radius of the Earth), we can use the principle of conservation of energy. Here’s a step-by-step solution:
Step 1: Understand the Energy Conservation Principle
The total mechanical energy (potential energy + kinetic energy) of the body remains constant if we ignore air resistance. Initially, the body has gravitational potential energy and no kinetic energy since it is released from rest.
Step 2: Calculate Initial Potential Energy
The gravitational potential energy U at a distance r from the center of the Earth is given by:
Ui=−GMmr
where:
- G is the universal gravitational constant,
- M is the mass of the Earth,
- m is the mass of the body,
- r is the distance from the center of the Earth.
Step 3: Calculate Final Potential Energy
When the body strikes the surface of the Earth (at a distance R from the center), the potential energy Uf is:
Uf=−GMmR
Step 4: Calculate Kinetic Energy at the Surface
When the body reaches the surface, it has kinetic energy K given by:
K=12mv2
where v is the velocity of the body just before it strikes the surface.
Step 5: Apply Conservation of Energy
According to the conservation of energy:
Ui+Ki=Uf+Kf
Since the body is released from rest, Ki=0:
−GMmr+0=−GMmR+12mv2
Step 6: Simplify the Equation
Rearranging the equation gives:
−GMmr+GMmR=12mv2
Factoring out m (which can be canceled since m≠0):
−GMr+GMR=12v2
Step 7: Solve for v2
Rearranging gives:
GMR−GMr=12v2
GMR−GMr=GMRr(r−R)
Thus,
GMRr(r−R)=12v2
Step 8: Solve for v
Multiplying both sides by 2:
2GMRr(r−R)=v2
Taking the square root gives:
v=√2GMRr(r−R)
Final Answer
The velocity of the body when it strikes the surface of the Earth is:
v=√2GMRr(r−R)
The total mechanical energy (potential energy + kinetic energy) of the body remains constant if we ignore air resistance. Initially, the body has gravitational potential energy and no kinetic energy since it is released from rest.
The gravitational potential energy U at a distance r from the center of the Earth is given by:
Ui=−GMmr
where:
- G is the universal gravitational constant,
- M is the mass of the Earth,
- m is the mass of the body,
- r is the distance from the center of the Earth.
When the body strikes the surface of the Earth (at a distance R from the center), the potential energy Uf is:
Uf=−GMmR
When the body reaches the surface, it has kinetic energy K given by:
K=12mv2
where v is the velocity of the body just before it strikes the surface.
According to the conservation of energy:
Ui+Ki=Uf+Kf
Since the body is released from rest, Ki=0:
−GMmr+0=−GMmR+12mv2
Rearranging the equation gives:
−GMmr+GMmR=12mv2
Factoring out m (which can be canceled since m≠0):
−GMr+GMR=12v2
Rearranging gives:
GMR−GMr=12v2
GMR−GMr=GMRr(r−R)
Thus,
GMRr(r−R)=12v2
Multiplying both sides by 2:
2GMRr(r−R)=v2
Taking the square root gives:
v=√2GMRr(r−R)
The velocity of the body when it strikes the surface of the Earth is:
v=√2GMRr(r−R)
Topper's Solved these Questions
- GRAVITATIONBook:CBSE COMPLEMENTARY MATERIALChapter:GRAVITATIONExercise:MULTIPLE CHOICE QUESTIONS
Explore 19 Videos
- GRAVITATIONBook:CBSE COMPLEMENTARY MATERIALChapter:GRAVITATIONExercise:LONG ANSWER TYPE QUESTIONS (5 MARKS)
Explore 6 Videos
- DIMENSIONS AND MEASUREMENT Book:CBSE COMPLEMENTARY MATERIALChapter:DIMENSIONS AND MEASUREMENT Exercise:M.C.Q PHYSICAL WORLD & MEASUREMENT
Explore 20 Videos
- KINEMATICSBook:CBSE COMPLEMENTARY MATERIALChapter:KINEMATICSExercise:M.C.Q.
Explore 20 Videos
Similar Questions
The earth has mass M and radius R .An object of mass m is dropped from a distance of 3R, from the centre of the earth.The object strikes the surface of the earth with a speed ,v=√kgR,where g is acceleration due to gravity or the surface of the earth.The value of k
View SolutionThe escape velocity of a body from the surface of the earth is equal to
View Solution
Knowledge Check
Statement-1 : A body released from a height equal to the radius (R) of the earth. The velocity of the body when it strikes the surface of the earth will be √2gR.
Statement -2 : As υ2=u2+2 as.AStatement -1 is true , Statement -2 is true , Statement-2 is a correct explanation of Statement -1.BStatement -1 is true , Statement-2 is true , Statement-2 is a correct explanation of Statement-1.CStatement-1 is true , Statement-2 is false.DStatement-1 is false , Statement-2 is true.The gravitational potential energy at a body of mass m at a distance r from the centre of the earth is U. What is the weight of the body at this distance ?
AUBUrCUrDU2rA body at rest starts from a point at a distance r (gtR) from the centre of the Earth. If M and R stand for the speed of the body when it reaches the Earth surface is
A√2GMRB√2GMR−rC√2GM(r−R)RrDZero
The satellite is moving round the earth (radius of earth = R) at a distance r from the centre of the earth. If g is the acceleration due to gravity on the surface of the earth. The acceleration of the satellite will be
View SolutionThe escape velocity of a body from the surface of earth is
View SolutionA body is released from a point of distance R' from the centre of earth. Its velocity at the time of striking the earth will be (R’>Re)
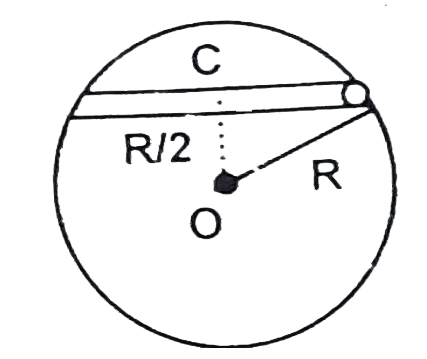
View SolutionA tunnel is dug across the earth of mass 'M' and radius 'R' at a distance R/2 from the centre 'O' of the Earth as shown. A body is released from rest from one end of the smooth tunnel. The velocity acquired by the body when it reaches the centre 'C' of the tunnel is
View SolutionThe acceleration of a body due to the attraction of the earth (radius R) at a distance 2R form the surface of the earth is (g=acceleration due to gravity at the surface of the earth)
View Solution