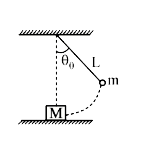
A simple pendulum , made of a string of length l and a bob of mass m, is released from a small angle $θ_{0}$ it strikes a block of mass M, kept on a horizontal surface at its lowest point of oscillations , elastically , it bounces back and goes up to an angle $θ_{1}$ then M is given by :

A

$\frac{m}{2} (\frac{θ_{0} + θ_{1}}{θ_{0} - θ_{1}})$

B

$m (\frac{θ_{0} - θ_{1}}{θ_{0} + θ_{1}})$

C

$m (\frac{θ_{0} + θ_{1}}{θ_{0} - θ_{1}})$

D

$\frac{m}{2} (\frac{θ_{0} - θ_{1}}{θ_{0} + θ_{1}})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$ω = \sqrt{\frac{g}{l}}$ .
Velocity just before collision $u = (\sqrt{\frac{g}{l}} θ_{0}) l = \sqrt{g l} θ_{0}$
v = velocity of ball after collision $v = (\sqrt{\frac{g}{l}} θ_{1}) l = \sqrt{g l} θ_{1}$ .
Momentum conservation : m u = Mv'-mv ………(i)
$e = 1 :$
$v' + v = u$ ......(ii)
$ω = \sqrt{\frac{g}{l}}$ From (i) and (ii)
$m (u + v) = M (u - v)$
$m (θ_{0} + θ_{1}) = M (θ_{0} - θ_{1})$
$M = m (\frac{θ_{0} + θ_{1}}{θ_{0} - θ_{1}})$ .
.

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

VMC MODULES ENGLISH-JEE MAIN REVISION TEST 8 (2020)-PHYSICS (SECTION 2)

Home
Ask Doubt
Profile