A stone tied to an inextensible string of length l=1m is kept horizontal. If it is released, find the angular speed of the stone when the string makes an angle θ=30∘ with horizontal.
To solve the problem of finding the angular speed of the stone when the string makes an angle of θ=30∘ with the horizontal, we can follow these steps:
Step 1: Understand the Forces Acting on the Stone
When the stone is released, it experiences two forces:
- The gravitational force acting downwards, mg.
- The tension in the string, T.
At the angle θ=30∘, we can resolve the gravitational force into two components:
- A component acting perpendicular to the string: mgcos(30∘).
- A component acting parallel to the string: mgsin(30∘).
Step 2: Set Up the Equations of Motion
The tension T in the string will balance the component of the weight acting perpendicular to the string:
T=mgcos(30∘)
The component of the weight acting parallel to the string provides the necessary centripetal force for circular motion:
mgsin(30∘)=mv2r
where r is the radius of the circular path, which is equal to the length of the string l=1m.
Step 3: Substitute the Values
Using the known values:
- cos(30∘)=√32
- sin(30∘)=12
We can rewrite the equations:
1. From the tension equation:
T=mg⋅√32
2. From the centripetal force equation:
mg⋅12=mv21
Simplifying gives:
g⋅12=v2
Thus, v2=g2.
Step 4: Relate Linear Speed to Angular Speed
The relationship between linear speed v and angular speed ω is given by:
v=rω
Since r=1m:
v=ω
Step 5: Substitute to Find Angular Speed
Substituting v into the equation:
ω=√v2=√g2
Final Result
Thus, the angular speed ω when the stone makes an angle of 30∘ with the horizontal is:
ω=√g2
When the stone is released, it experiences two forces:
- The gravitational force acting downwards, mg.
- The tension in the string, T.
- A component acting perpendicular to the string: mgcos(30∘).
- A component acting parallel to the string: mgsin(30∘).
The tension T in the string will balance the component of the weight acting perpendicular to the string:
T=mgcos(30∘)
mgsin(30∘)=mv2r
where r is the radius of the circular path, which is equal to the length of the string l=1m.
Using the known values:
- cos(30∘)=√32
- sin(30∘)=12
1. From the tension equation:
T=mg⋅√32
mg⋅12=mv21
Simplifying gives:
g⋅12=v2
Thus, v2=g2.
The relationship between linear speed v and angular speed ω is given by:
v=rω
Since r=1m:
v=ω
Substituting v into the equation:
ω=√v2=√g2
Thus, the angular speed ω when the stone makes an angle of 30∘ with the horizontal is:
ω=√g2
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Solved Examples
7 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.1
15 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A stone tied to a string of length l is whirled in a horizontal circle at a constant angular speed ω in a circle of radius r. If the string makes an angle θ with vertical then the tension in the string is :
View SolutionA particle of mass m is attached to the celling of a cabin with an inextensible light string of length l. The cabin is moving upward with an acceleration a . The particle is taken to a position such that string makes an angle θ with vertical. When string becomes vertical, find the tension in the string.

View Solution
Knowledge Check
A stone of mass 5 kg is tied to a string of length 10 m is whirled round in a horizontal circle. What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N?
A10ms−1B15ms−1C20ms−1D25ms−1
A heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
View SolutionThe block A is moving downward with constant velocity v0. Find the velocity of the block B. When the string makes an angle θ with the horizontal

View SolutionA stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
View SolutionA stone hanging from a massless string of length 15 m is projected horizontally with speed 12ms−1. The speed of the particle at the point where the tension in the string is equal to the weight of the particle, is close to
View SolutionA bob hangs from a rigid support by an inextensible string of length l. It is released from rest when string makes an agngle 60∘ with vertical . The speed of the bob at the lowest position is
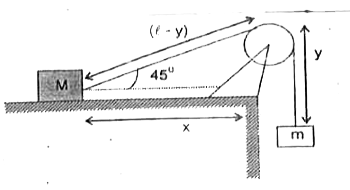
View SolutionTwo masses M and m are connected by a light inextensible string which passes over a small pulley as shown in the diagram. If the mass m is moving downward with a velocity v when the string makes an angle of 45∘ with the horizontal, find the total K.E. of the two masses. AsSigmae that the mass M moves horizontally.
View SolutionA stone hanging from a massless string of length 15m is projected horizontally with speed √147ms−1 Then the Speed of the particle, at the point where tension in string equals the weight of particle, is
View Solution
