Assertion : Bob is released from rest position A. Given θ0 very small. Angular velocity of bob about point O is maximum and (√gl)θ0 at point O.
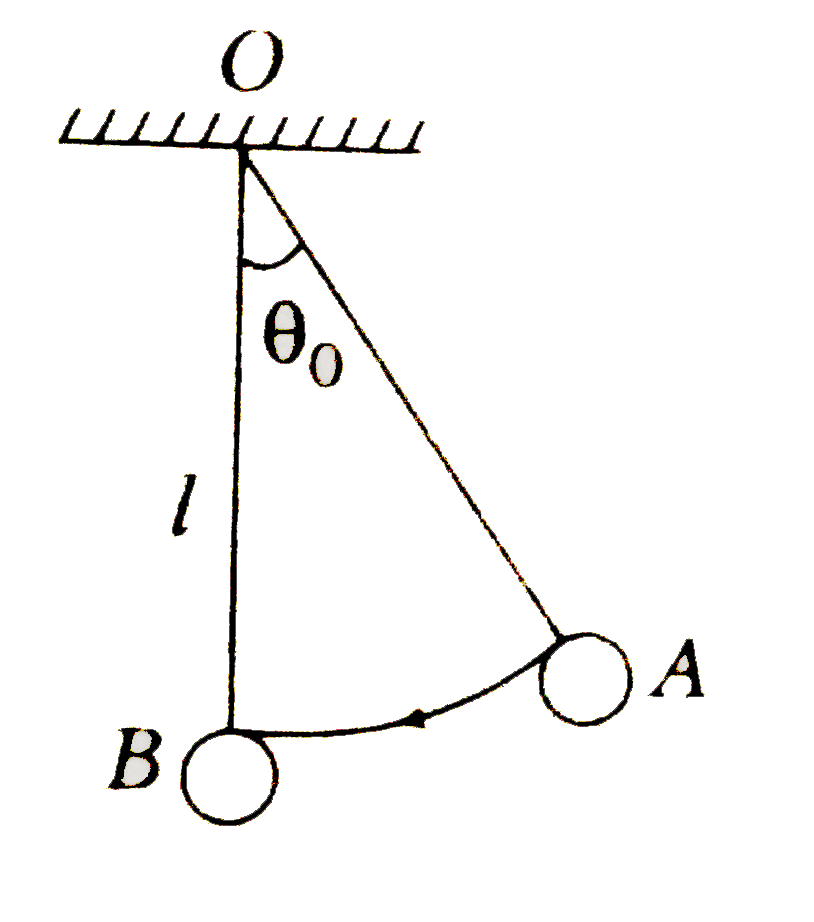
Reason : For small angular amplitudes , motion of bob is simple harmonic
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is true.
The correct Answer is:B
(b) Maximum angular velocity =ωθ0
=(2πf)θ0=(2π)(12π√gl)θ0
=(√gl)θ0
Similar Questions
(i) A simple pendulum consist of a small bob of mass m tied to a string of length L. Show that the total energy of oscillation of the pendulum is E≅12mgLθ20 when it is oscillating with a small angular amplitude θ0. Assume the gravitational potential energy to be zero of the lowest position of the bob. (ii) Three identical pendulums A, B and C are suspended from the ceiling of a room. They are swinging in semicircular arcs in vertical planes. The string of pendulum A snaps when it is vertical and it was found that the bob fell on the floor with speed V1. The string of B breaks when it makes an angle of 30° to the vertical and the bob hits the floor with speed V2. The string of pendulum C was cut when it was horizontal and the bob falls to the floor hitting it with a speed V3. Which is greatest and which is smallest among V1,V2 and V3?
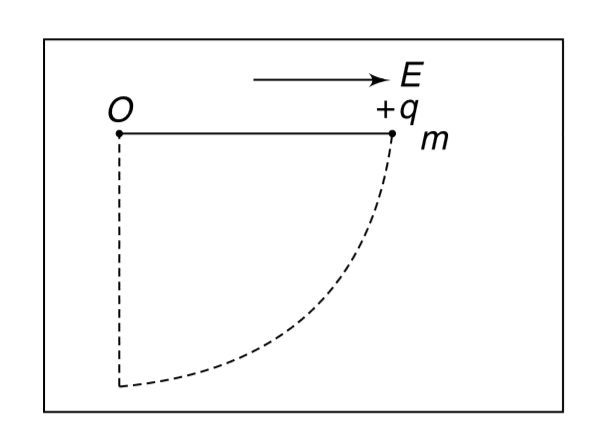
View SolutionThere is a uniform horizontal electric field of strength E in a region. A pendulum bob is pulled to make the string horizontal and released. The bob has mass m and charge q. (a) Find the maximum angle (θ0) that the bob swings before coming to rest momentarily. (b) Find E if the bob comes to rest when the string is vertical.
View Solution
Knowledge Check
A simple pendulum of mass m and length L is held in horizontal position. If it is released from this position, then find the angular momentum of the bob about the point of suspension when it is vertically below the point of suspension.
AmL√2gLBmL√gLCmL√3gLDnoneA pendulum of length l=1m is released from θ0=60∘ . The rate of change of speed of the bob at θ=30∘ is.
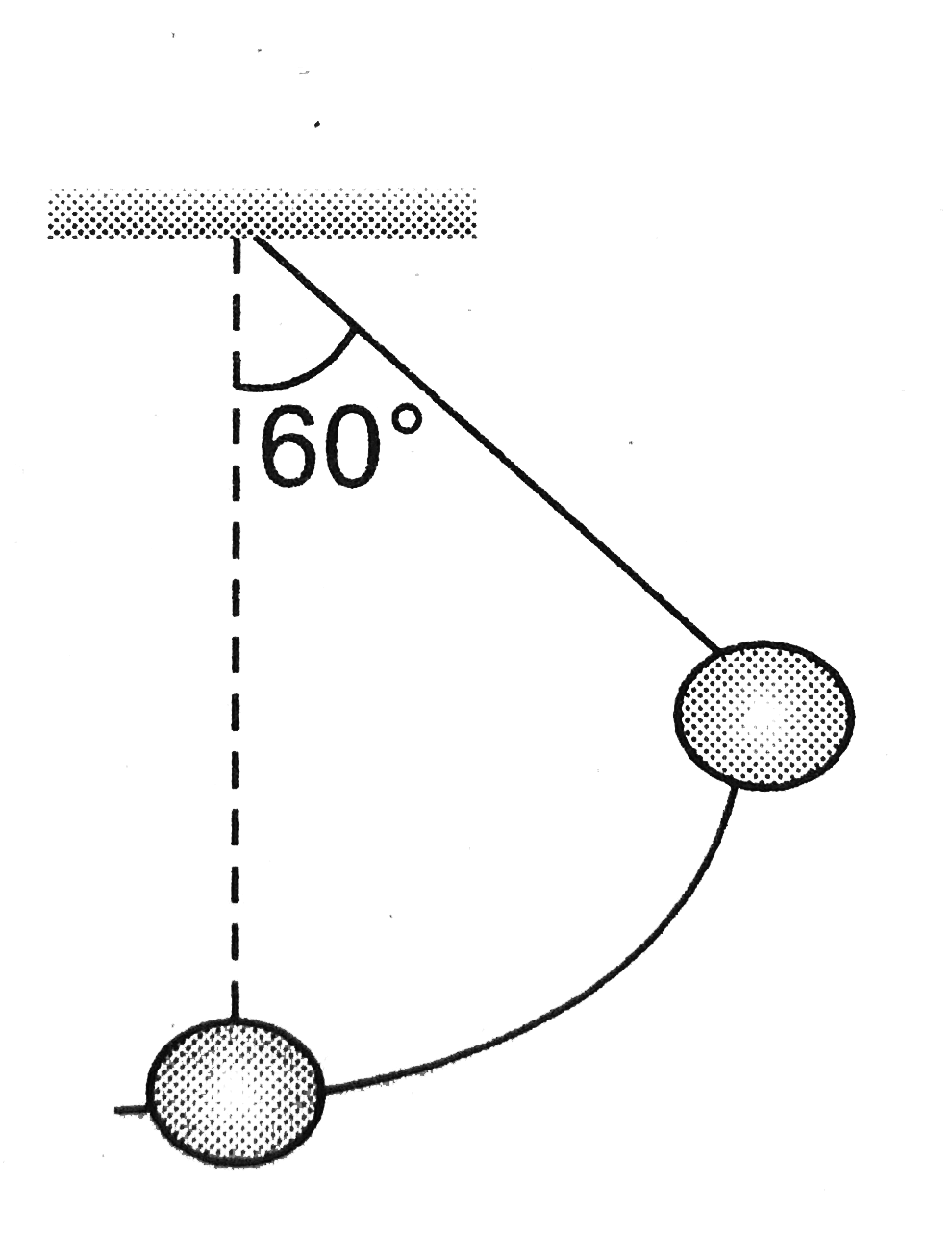 A5√3m/s2B5m/s2C10m/s2D2.5m/s2
A5√3m/s2B5m/s2C10m/s2D2.5m/s2Assertion : For an oscillating simple pendulum, the tension in the string is maximum at the mean position and minimum at the extreme position. lt brgt Reason : The velocity of oscillating bob in simple harmonic motion is maximum at the mean position.
AIf both assertion and reason are true and the reason is the correct explanation of the assertion.BIf both assertion and reason are true but reason is not the correct explanation of the assertion.CIf assertion is true but reason is false.DIf the assertion and reason both are false
A simple pendulum is released from rest with the string in horizontal position. The vertical component of the velocity of the bob becomes maximum, when the string makes an angle θ with the vertical. The angle θ is equal to
View SolutionThe angular amplitude of a simple pendulum is θ0. The maximum tension in its string will be
View SolutionA simple pendulum has a string of length l and bob of mass m. When the bob is at its lowest position , it is given the minimum horizontal speed necessary for it to move in a circular path about the point point of suspension. The tension in the string at the lowest position if the bob is
View SolutionIf a simple pendulum of length l has maximum angular displacement θ, then the maximum velocity of the bob is
View SolutionIf 'V' be the maximum velocity of the bob of a pendulum and 'h' the maximum height of the bob from its point of rest, then
View Solution