A body of mass 0.10kg is attached to vertical massless spring with force constant 4.0×103N/m. The body is displaced 10.0cm from its equilibrium position and released. How much time elapses as the body moves from a point 8.0cm on one side of the equilibrium position to a point 6.0cm on the same side of the equilibrium position ?
The correct Answer is:A, C, D
To solve the problem step by step, we will follow these steps:
Step 1: Calculate the angular frequency (ω)
The angular frequency of the oscillation is given by the formula:
ω=√km
Where:
- k=4.0×103N/m (spring constant)
- m=0.10kg (mass)
Substituting the values:
ω=√4.0×1030.10=√40000=200rad/s
Step 2: Write the equation of motion for SHM
The general equation for simple harmonic motion (SHM) can be expressed as:
x(t)=Asin(ωt)
Where:
- A=10cm=0.10m (amplitude)
- ω=200rad/s
Thus, the equation becomes:
x(t)=0.10sin(200t)
Step 3: Find the time t1 when the displacement is 8cm
Set x(t1)=0.08m:
0.08=0.10sin(200t1)
sin(200t1)=0.080.10=0.8
Now, taking the inverse sine:
200t1=arcsin(0.8)
Calculating arcsin(0.8):
200t1≈0.927radians
Thus,
t1=0.927200≈0.004635s=4.635ms
Step 4: Find the time t2 when the displacement is 6cm
Set x(t2)=0.06m:
0.06=0.10sin(200t2)
sin(200t2)=0.060.10=0.6
Now, taking the inverse sine:
200t2=arcsin(0.6)
Calculating arcsin(0.6):
200t2≈0.6435radians
Thus,
t2=0.6435200≈0.0032175s=3.218ms
Step 5: Calculate the time elapsed Δt
The time elapsed as the body moves from 8cm to 6cm is given by:
Δt=t2−t1
Substituting the values:
Δt=3.218ms−4.635ms≈−1.417ms
Since we are considering the absolute time elapsed:
Δt≈1.417ms
Final Answer
The time elapsed as the body moves from 8.0cm to 6.0cm is approximately 1.42ms.
---
The angular frequency of the oscillation is given by the formula:
ω=√km
Where:
- k=4.0×103N/m (spring constant)
- m=0.10kg (mass)
ω=√4.0×1030.10=√40000=200rad/s
The general equation for simple harmonic motion (SHM) can be expressed as:
x(t)=Asin(ωt)
Where:
- A=10cm=0.10m (amplitude)
- ω=200rad/s
x(t)=0.10sin(200t)
Set x(t1)=0.08m:
0.08=0.10sin(200t1)
sin(200t1)=0.080.10=0.8
Now, taking the inverse sine:
200t1=arcsin(0.8)
Calculating arcsin(0.8):
200t1≈0.927radians
Thus,
t1=0.927200≈0.004635s=4.635ms
Set x(t2)=0.06m:
0.06=0.10sin(200t2)
sin(200t2)=0.060.10=0.6
Now, taking the inverse sine:
200t2=arcsin(0.6)
Calculating arcsin(0.6):
200t2≈0.6435radians
Thus,
t2=0.6435200≈0.0032175s=3.218ms
The time elapsed as the body moves from 8cm to 6cm is given by:
Δt=t2−t1
Substituting the values:
Δt=3.218ms−4.635ms≈−1.417ms
Since we are considering the absolute time elapsed:
Δt≈1.417ms
The time elapsed as the body moves from 8.0cm to 6.0cm is approximately 1.42ms.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Level 2 Single Correct
Explore 28 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Level 2 More Than One Correct
Explore 8 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Level 1 Single Correct
Explore 24 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEY ENGLISHChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
A cart of mass 2.00kg is attached to the end of a horizontal spring with force constant k=150N/m. The cart is displaced 15.0cm from its equilibrium position and released. What are
(a) the amplitude (b) the period ( c) the mechanical energy (e) the maximum velocity of the cart ? Neglect friction.
View SolutionA 10 kg metal block is attached to a spring constant 1000Nm−1. A block is displaced from equilibrium position by 10 cm and released. The maximum acceleration of the block is
View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximum speed of the trolley is
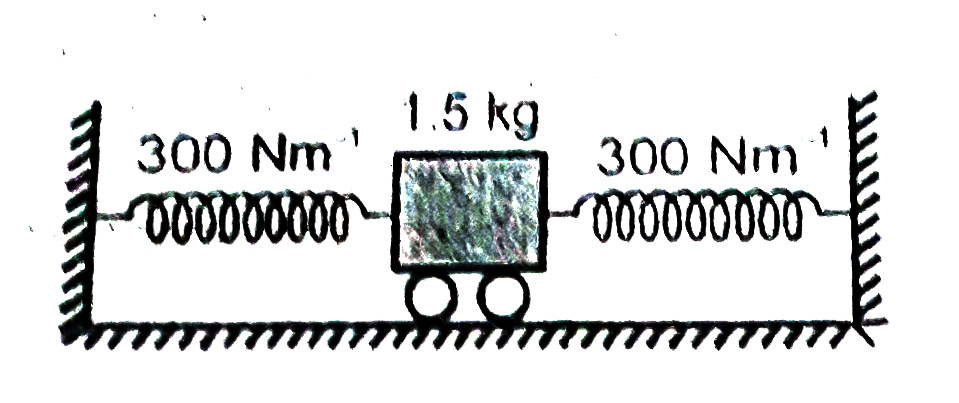
View SolutionA body of mass 100 g is attached to a hanging spring force constant is 10N/m. The body is lifted until the spring is in its unstretched state and then released. Calculate the speed of the body when it strikes the table 15cm below the release point .
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is

View SolutionA system shown in the figure consists of a massless pulley, a spring of force constant k displaced vertically downwards from its equilibrium position and released, then the Period of vertical oscillations is

View SolutionA block of mass 4kg hangs from a spring of force constant k=400N/m. The block is pulled down 15cm below equilibrium and relesed. How long does it take block to go from 12cm below equilibrium (on the way up) to 9cm above equilibrium ?
View Solution