A body of mass 100 g is attached to a hanging spring force constant is 10N/m. The body is lifted until the spring is in its unstretched state and then released. Calculate the speed of the body when it strikes the table 15cm below the release point .
1m/s
0.866m/s
0.225m/s
1.5m/s
The correct Answer is:B
To solve the problem, we will use the principle of conservation of energy. The energy in the system will be conserved as the body falls and strikes the table.
1. Identify the Given Data:
- Mass of the body, m=100g=0.1kg
- Spring constant, k=10N/m
- Distance fallen, h=15cm=0.15m
2. Initial Energy:
- When the body is lifted to the unstretched position of the spring, the initial energy of the system is zero because the spring is not stretched and the body is at rest.
3. Final Energy:
- When the body strikes the table, the final energy consists of:
- Kinetic energy of the body: KE=12mv2
- Potential energy of the body at the height of the table: PE=−mgh (negative because it is below the reference point)
- Elastic potential energy stored in the spring when it is stretched: PEspring=12kx2 where x=0.15m
4. Setting Up the Energy Conservation Equation:
Initial Energy=Final Energy
0=12kx2+12mv2−mgh
5. Substituting Values:
- Substitute k=10N/m, x=0.15m, m=0.1kg, g=10m/s2, and h=0.15m:
0=12⋅10⋅(0.15)2+12⋅0.1⋅v2−0.1⋅10⋅0.15
6. Calculating Each Term:
- Calculate 12⋅10⋅(0.15)2:
=0.5⋅10⋅0.0225=0.1125J
- Calculate −0.1⋅10⋅0.15:
=−0.1⋅10⋅0.15=−0.15J
7. Rearranging the Equation:
0=0.1125+12⋅0.1⋅v2−0.15
12⋅0.1⋅v2=0.15−0.1125
12⋅0.1⋅v2=0.0375
8. Solving for v2:
0.1⋅v2=0.075
v2=0.0750.1=0.75
9. Finding v:
v=√0.75≈0.866m/s
Final Answer:
The speed of the body when it strikes the table is approximately 0.866 m/s.
- Mass of the body, m=100g=0.1kg
- Spring constant, k=10N/m
- Distance fallen, h=15cm=0.15m
- When the body is lifted to the unstretched position of the spring, the initial energy of the system is zero because the spring is not stretched and the body is at rest.
- When the body strikes the table, the final energy consists of:
- Kinetic energy of the body: KE=12mv2
- Potential energy of the body at the height of the table: PE=−mgh (negative because it is below the reference point)
- Elastic potential energy stored in the spring when it is stretched: PEspring=12kx2 where x=0.15m
Initial Energy=Final Energy
0=12kx2+12mv2−mgh
- Substitute k=10N/m, x=0.15m, m=0.1kg, g=10m/s2, and h=0.15m:
0=12⋅10⋅(0.15)2+12⋅0.1⋅v2−0.1⋅10⋅0.15
- Calculate 12⋅10⋅(0.15)2:
=0.5⋅10⋅0.0225=0.1125J
- Calculate −0.1⋅10⋅0.15:
=−0.1⋅10⋅0.15=−0.15J
0=0.1125+12⋅0.1⋅v2−0.15
12⋅0.1⋅v2=0.15−0.1125
12⋅0.1⋅v2=0.0375
0.1⋅v2=0.075
v2=0.0750.1=0.75
v=√0.75≈0.866m/s
The speed of the body when it strikes the table is approximately 0.866 m/s.
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 subjective
27 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Objective
30 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 Assertion And Reason
12 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
A block of mass m = 2 kg is attached to two unstretched spring of force constant k1=100N/m and k2=125N/m
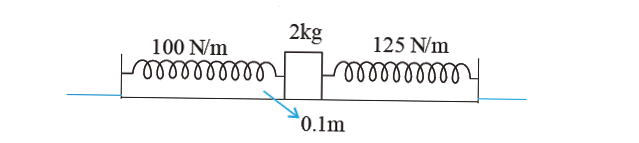
The block is displaced towards left through a distance of 10 cm and released. Find the speed of the block as it passes through the mean position.
View SolutionA body of mass 0.10kg is attached to vertical massless spring with force constant 4.0×103N/m. The body is displaced 10.0cm from its equilibrium position and released. How much time elapses as the body moves from a point 8.0cm on one side of the equilibrium position to a point 6.0cm on the same side of the equilibrium position ?
View SolutionA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is

View Solution
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will be
View SolutionPassage VIII A disc of mass m and radius R is attached with a spring of force contant k at its center as shown in figure. At x-0, spring is unstretched. The disc is moved to x=A and then released. There is no slipping between disc and ground. Let f be the force of friction on the disc from the ground.

f versus t (time) graph will be as
View SolutionA small ball of mass M=1 kg is attached to two identical springs of constant 100N/m, which are attached to floor and roof. The springs are initially unstretched. By what distance ball comes down to attain equilibrium? (in cm)

View SolutionA ball of mass m is attached to the lower end of a light vertical spring of force constant K. The upper end of the spring is fixed. The ball is released from rest with the spring at its normal ( unstretched ) length, and comed to rest again after descending through a distance x.
View SolutionA particle of mass m is attached with three springs A,B and C of equal force constancts k as shown in figure. The particle is pushed slightly against the spring C and released. Find the time period of oscillation.
 .
.
View SolutionA block of mass 100g attached to a spring of stiffness 100N/m is lying on a frictionless floor as shown. The block is moved to compress the spring by 10cm and released. If the collision with the wall is elastic then find the time period of oscillations.

View SolutionA block of mass m attached in the lower and vertical spring The spring is hung from a calling and force constant value k The mass is released from rest with the spring initially unstreched The maximum value of extension produced in the length of the spring will be
View Solution
