An ideal massless spring S can compressed m in equilibrium by a force of . This same spring is placed at the bottom of a friction less inclined plane which makes an angle with the horizontal. A mass is released from the rest at top of the inclined plane and is brought to rest momentarily after compressing the spring by the distance through which the mass moved before coming to rest is.
The correct Answer is:C
To solve the problem, we will use the principle of conservation of energy. The energy lost by the mass as it moves down the incline will be equal to the energy stored in the spring when it is compressed.
1. Determine the Spring Constant (k):
The spring constant k can be calculated using the information given. The spring is compressed by 1.0m under a force of 1000N.
k=Fx=1000N1.0m=1000N/m
2. Calculate the Potential Energy at the Top of the Incline:
The mass m=10kg is released from rest. The height h from which it falls can be expressed in terms of the distance d it travels down the incline and the angle θ=30∘:
h=dsin(30∘)=d2
The potential energy at the top is given by:
PE=mgh=mg(d2)=10⋅9.81⋅d2=49.05dJ
3. Calculate the Energy Stored in the Spring:
When the spring is compressed by 2.0m, the energy stored in the spring is:
Es=12kx2=12⋅1000⋅(2.0)2=12⋅1000⋅4=2000J
4. Apply Conservation of Energy:
The potential energy at the top of the incline will equal the energy stored in the spring when the mass comes to rest:
PE=Es
49.05d=2000
5. Solve for d:
d=200049.05≈40.7m
6. Calculate Total Distance Travelled:
The total distance travelled by the mass before coming to rest is:
Total Distance=d+2=40.7+2=42.7m
Final Answer:
The distance through which the mass moved before coming to rest is approximately 42.7m.
The spring constant k can be calculated using the information given. The spring is compressed by 1.0m under a force of 1000N.
k=Fx=1000N1.0m=1000N/m
The mass m=10kg is released from rest. The height h from which it falls can be expressed in terms of the distance d it travels down the incline and the angle θ=30∘:
h=dsin(30∘)=d2
The potential energy at the top is given by:
PE=mgh=mg(d2)=10⋅9.81⋅d2=49.05dJ
When the spring is compressed by 2.0m, the energy stored in the spring is:
Es=12kx2=12⋅1000⋅(2.0)2=12⋅1000⋅4=2000J
The potential energy at the top of the incline will equal the energy stored in the spring when the mass comes to rest:
PE=Es
49.05d=2000
d=200049.05≈40.7m
The total distance travelled by the mass before coming to rest is:
Total Distance=d+2=40.7+2=42.7m
The distance through which the mass moved before coming to rest is approximately 42.7m.
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 subjective
27 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Objective
30 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 Assertion And Reason
12 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
An ideal massless spring S can compressed 1.0 m in equilibrium by a force of 100N. This same spring is placed at the bottom of a friction less inclined plane which makes an angle θ=30∘ with the horizontal. A (10 kg) mass (m) is released from rest at the top of the incline and and is brought to rest momentarily after compressing the spring by 2m.ifg =10 ms^(-1), what is the speed of just before it touches the spring?
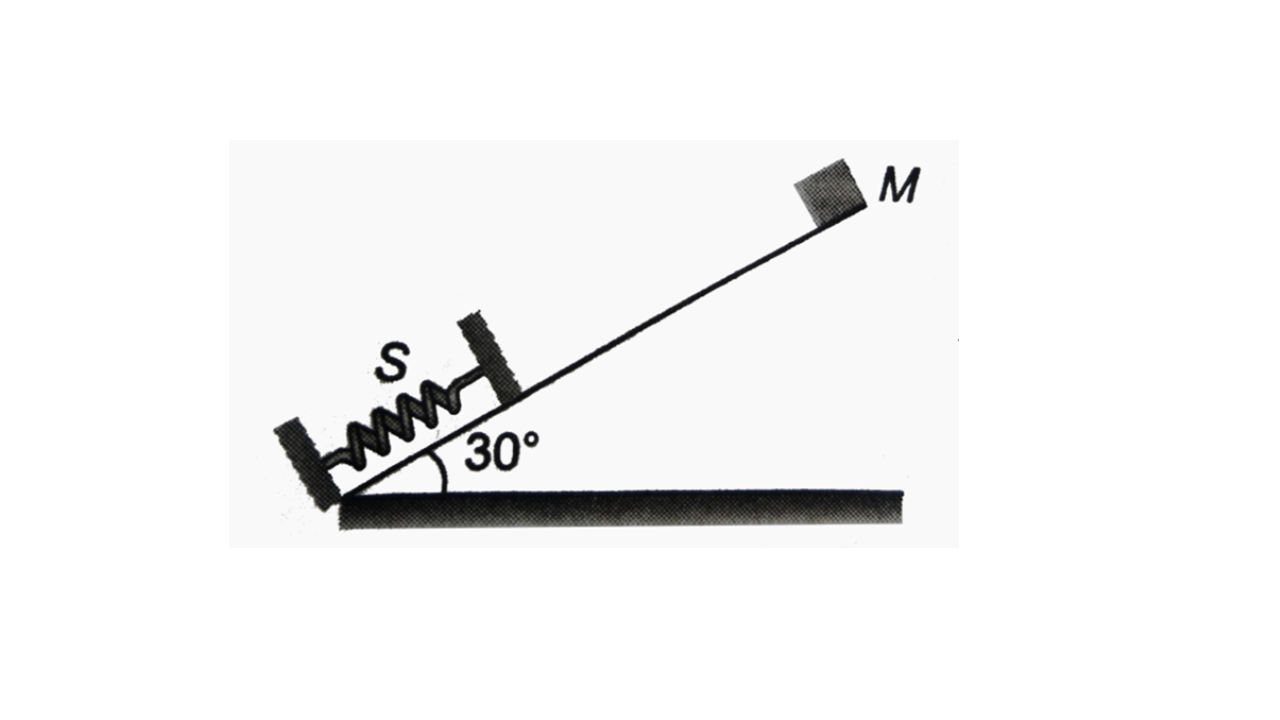 .
.
View SolutionAn ideal massles spring S can be compressed 1 m by a force of 100 N in equilibrium. The same spring is placed at the bottom of a frictionless plane inclined at 30∘ to the horizontal. A 10 kg block M is released from rest at the top of the incline and is brought to rest momentarily after compressing the spring by 2 m. If g=10m/s2, the speed of mass just before it touches the spring is √10xm/s. Find value of x?

View Solution
Knowledge Check
A block mass 3 kg slides down a frictionless inclined plane of length 6 m and height 4 m. if the block is released from rest at the top of the incline, what is its speed at the bottom?
A5m/sB6m/sC8m/sD9m/sA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A10.3NB23.8NC11.9ND6.3N
A block of mass 2 kg rests on a rough inclined plane making an angle of 30° with the horizontal. If μS=0.6 , what is the frictional force on the block ?
View SolutionA triangular prism of mass m placed on it is released from rest on a smooth inclined plane of inclination θ The block does not slip on the prism. Then
View SolutionA block of mass √2 kg is released from the top of an inclined smooth surface as shown in fighre. If spring constant of spring is 100 N/m and block comes to rest after compressing the spring by 1 m, then the distance travelled by block befor it comes to rest is
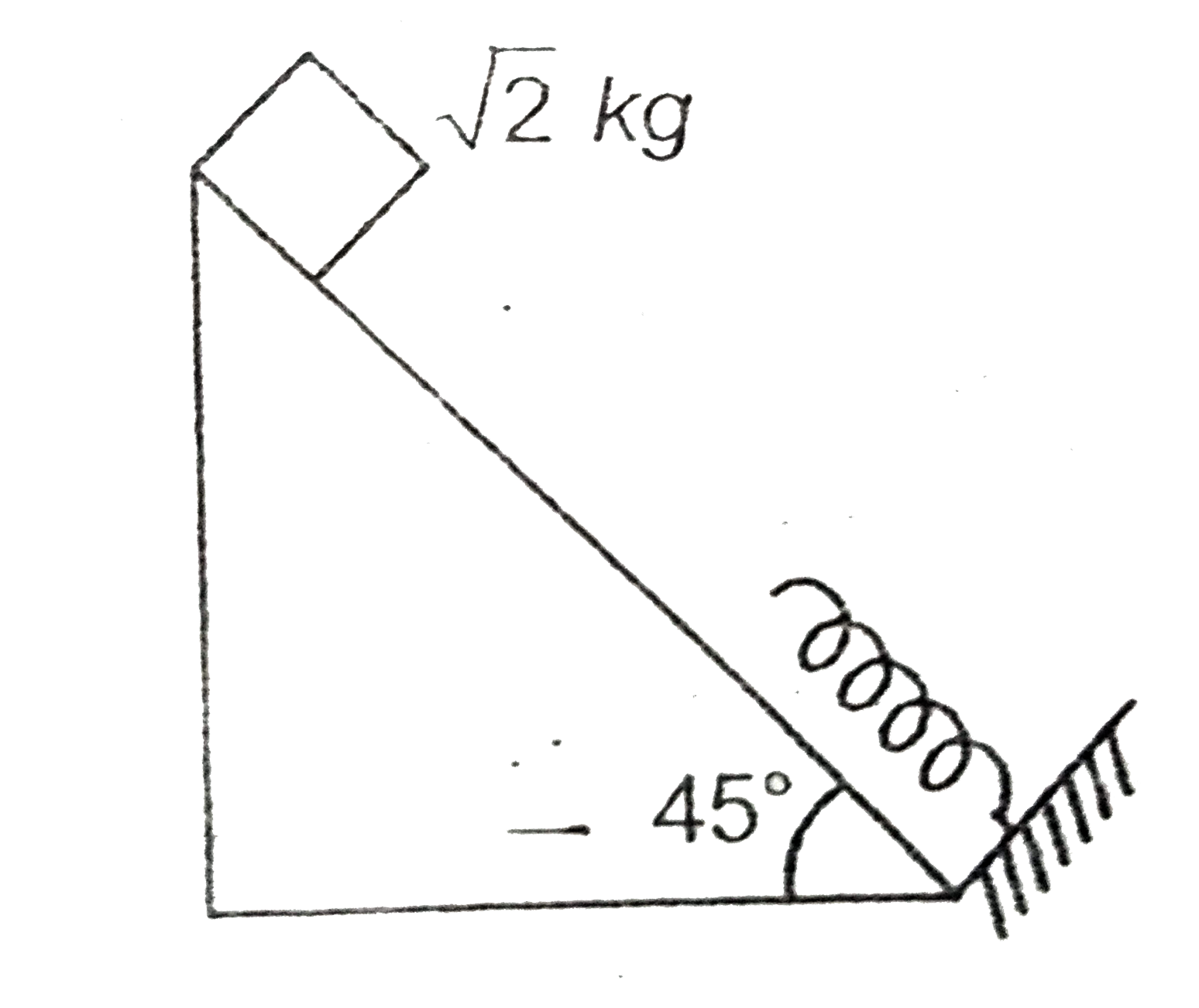
View SolutionA block of mass √2 kg is released from the top of an inclined smooth surface as shown in fighre. If spring constant of spring is 100 N/m and block comes to rest after compressing the spring by 1 m, then the distance travelled by block befor it comes to rest is

View SolutionA block of mass 4 kg is released from the top of an inclined smooth surface as shown in figure If spring constant of spring is 100N/m and block comes to rest after compressing spring by 1 m, find the distance travelled by the block before it comes t o rest.

View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View Solution
