An ideal massless spring S can compressed 1.0 m in equilibrium by a force of 100N. This same spring is placed at the bottom of a friction less inclined plane which makes an angle θ=30∘ with the horizontal. A (10 kg) mass (m) is released from rest at the top of the incline and and is brought to rest momentarily after compressing the spring by 2m.ifg =10 ms^(-1), what is the speed of just before it touches the spring? 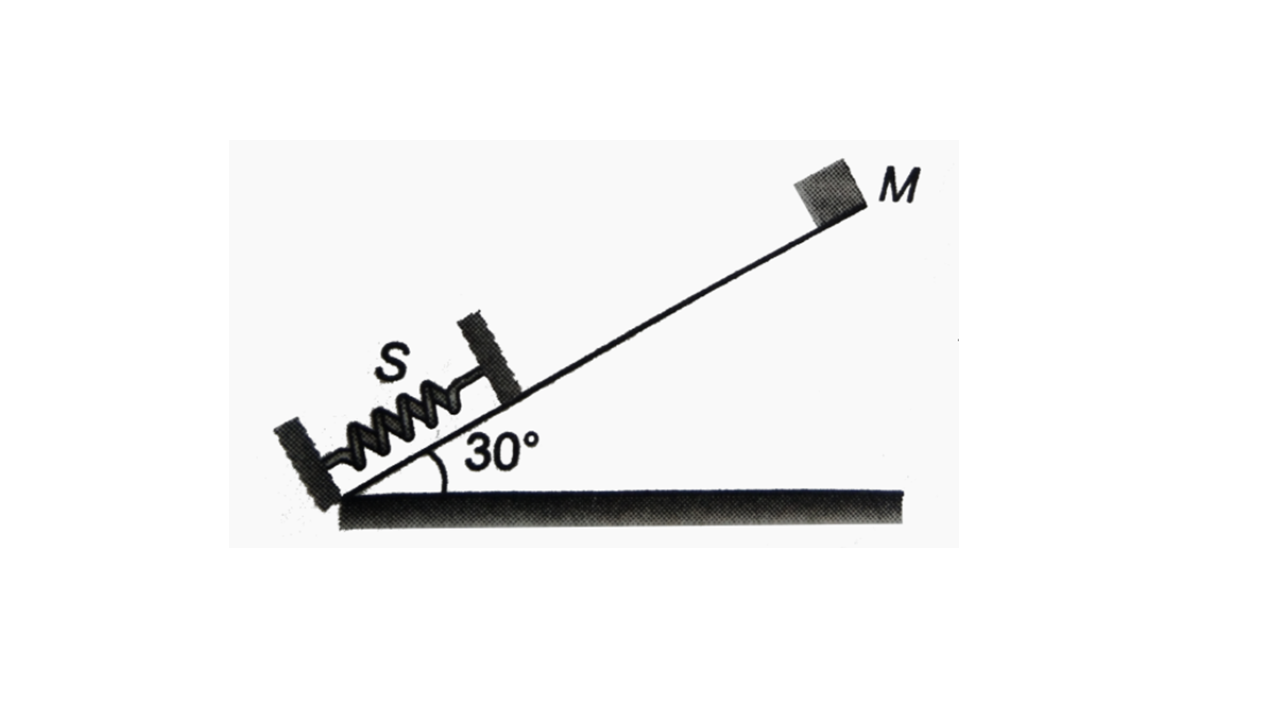 .
.
(a) √20ms−1
(b) √30ms−1
(c) √10ms−1
(d) √40ms−1
The correct Answer is:A
F=kx
∴k=Fx=1001
=100N/m
Ei=Ef
∴12×10×v2=12×100×(2)2−(10)(10)(2sin30∘)
Solving we get,
v=√20m/s
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 More Than One Correct
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Subjective
15 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 subjective
27 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
An ideal massless spring S can compressed 1.0 m in equilibrium by a force of 1000N. This same spring is placed at the bottom of a friction less inclined plane which makes an angle θ=30∘ with the horizontal. A 10kg mass m is released from the rest at top of the inclined plane and is brought to rest momentarily after compressing the spring by 2.0m. the distance through which the mass moved before coming to rest is.
View SolutionAn ideal massles spring S can be compressed 1 m by a force of 100 N in equilibrium. The same spring is placed at the bottom of a frictionless plane inclined at 30∘ to the horizontal. A 10 kg block M is released from rest at the top of the incline and is brought to rest momentarily after compressing the spring by 2 m. If g=10m/s2, the speed of mass just before it touches the spring is √10xm/s. Find value of x?

View Solution
Knowledge Check
A block mass 3 kg slides down a frictionless inclined plane of length 6 m and height 4 m. if the block is released from rest at the top of the incline, what is its speed at the bottom?
A5m/sB6m/sC8m/sD9m/s
A block of mass 2 kg rests on a rough inclined plane making an angle of 30° with the horizontal. If μS=0.6 , what is the frictional force on the block ?
View SolutionA block of mass √2 kg is released from the top of an inclined smooth surface as shown in fighre. If spring constant of spring is 100 N/m and block comes to rest after compressing the spring by 1 m, then the distance travelled by block befor it comes to rest is

View SolutionA block of mass √2 kg is released from the top of an inclined smooth surface as shown in fighre. If spring constant of spring is 100 N/m and block comes to rest after compressing the spring by 1 m, then the distance travelled by block befor it comes to rest is

View SolutionIn an ideal pulley particle system, mass m2 is connected with a vertical spring of stiffness k. If mass m2 is released from rest, when the spring is underformed, find the maximum compression of the spring.

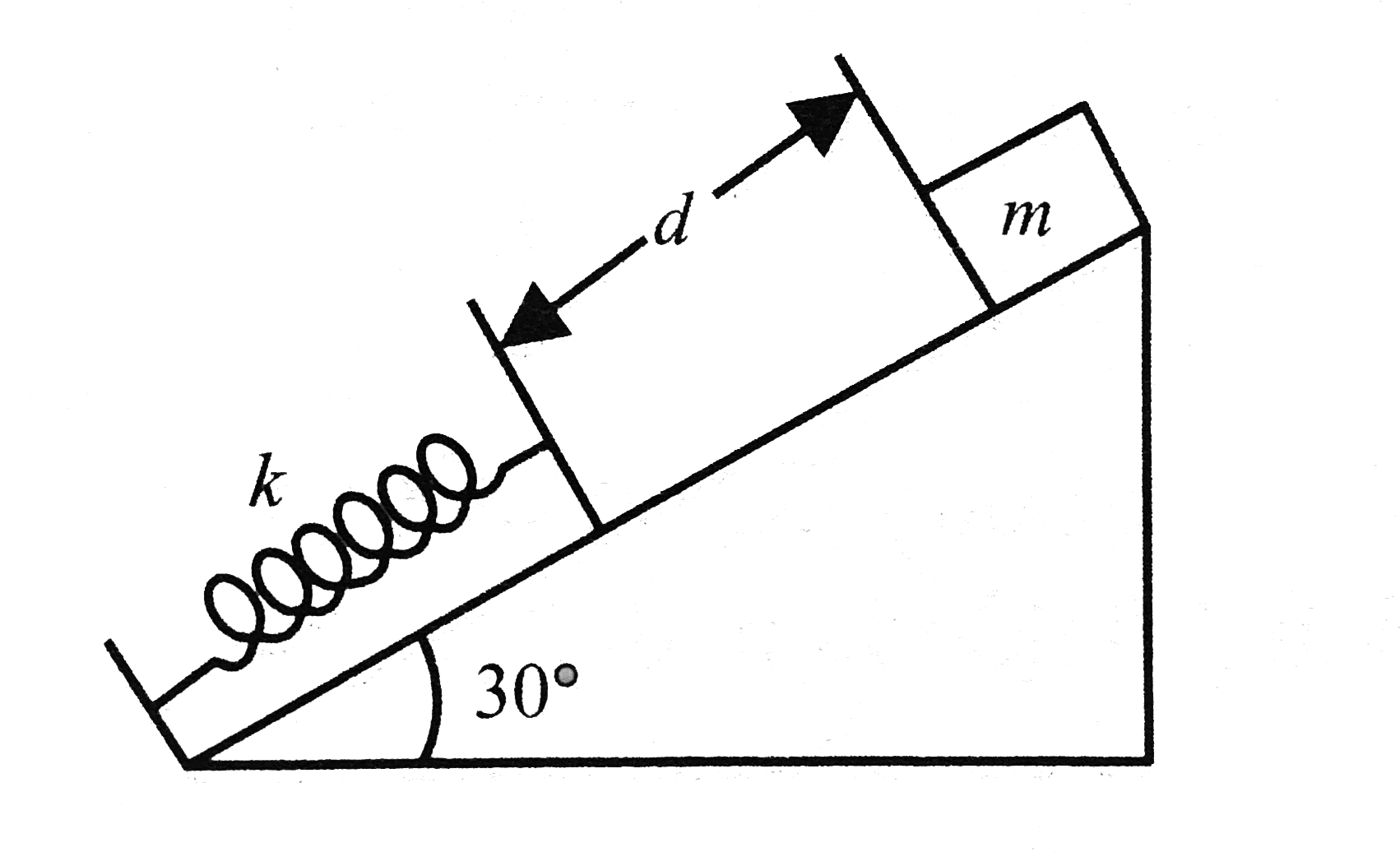
View SolutionA block of 4kg mass starts at rest and slides a distance d down a friction less incline ( angle 30∘) where it runs into a spring of negligible mass. The block slides an additional 25cm before it is brought to rest momentarily by compressing the spring. The force constant of the spring is 400Nm−1. The value of d is (take g=10ms−2)
View SolutionA block rests on a rough inclined plane making an angle of 30∘ with horizontal. The coefficient of static friction between the block and inclined plane is 0.8 . If the frictional force on the block is 10N, the mass of the block in kg is (g=10m/s2)
View SolutionThe upper half of an inclined plane with an angle of inclination theta, is smooth while the lower half is rough. A body starting from rest at the top of the inclined plane comes to rest at the bottom of the inclined plane. Then the coefficient of friction for the lower half is
View Solution
