Two large rigid vertical walls A and B are parallel to each other and separated by 10m. A particle of mass 10g is projected with an initial velocity of 20m/s at 45∘ to the horizontal from point P on the ground, such that AP=5m. The plane of motion of the particle is vertical and perpendicular to the walls. Assuming that all the collisions are perfectly elastic, find the maximum height attained by the particle and the total number of collisions suffered by the particle with the walls before it hits ground. Take g=10m/s2.

10 m, 4
20 m, 4
10 m, 5
30 m, 6
The correct Answer is:A
As the collisions are perfectly elastic, collsion of the ball will not affect the vertical component of its velocity while the horizontal component will be simply reserved.
Hence, Hmax=v2y2g=[20×sin45∘]22×10=10m
Total time of flight
T=2vyg=2×20×(1√2)10=2√2s
Total horizontal distance travelled before striking the ground x=vxT=40m
PB+BA+AB+BA+AB=45m
Hence, total number of collision suffered by the particle with the walls before it hits ground =4.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Comprehension Based Questions
Explore 3 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
Similar Questions
A particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View SolutionA particle is projected with velocity of 10ms at an angle of 15° with horizontal.The horizontal range will be(g=10ms2)
View SolutionThe particle of mass 1 kg is projected with velocity 20√2m/s at 45∘ with ground . When , the particle is at highest point (g=10m/s2),
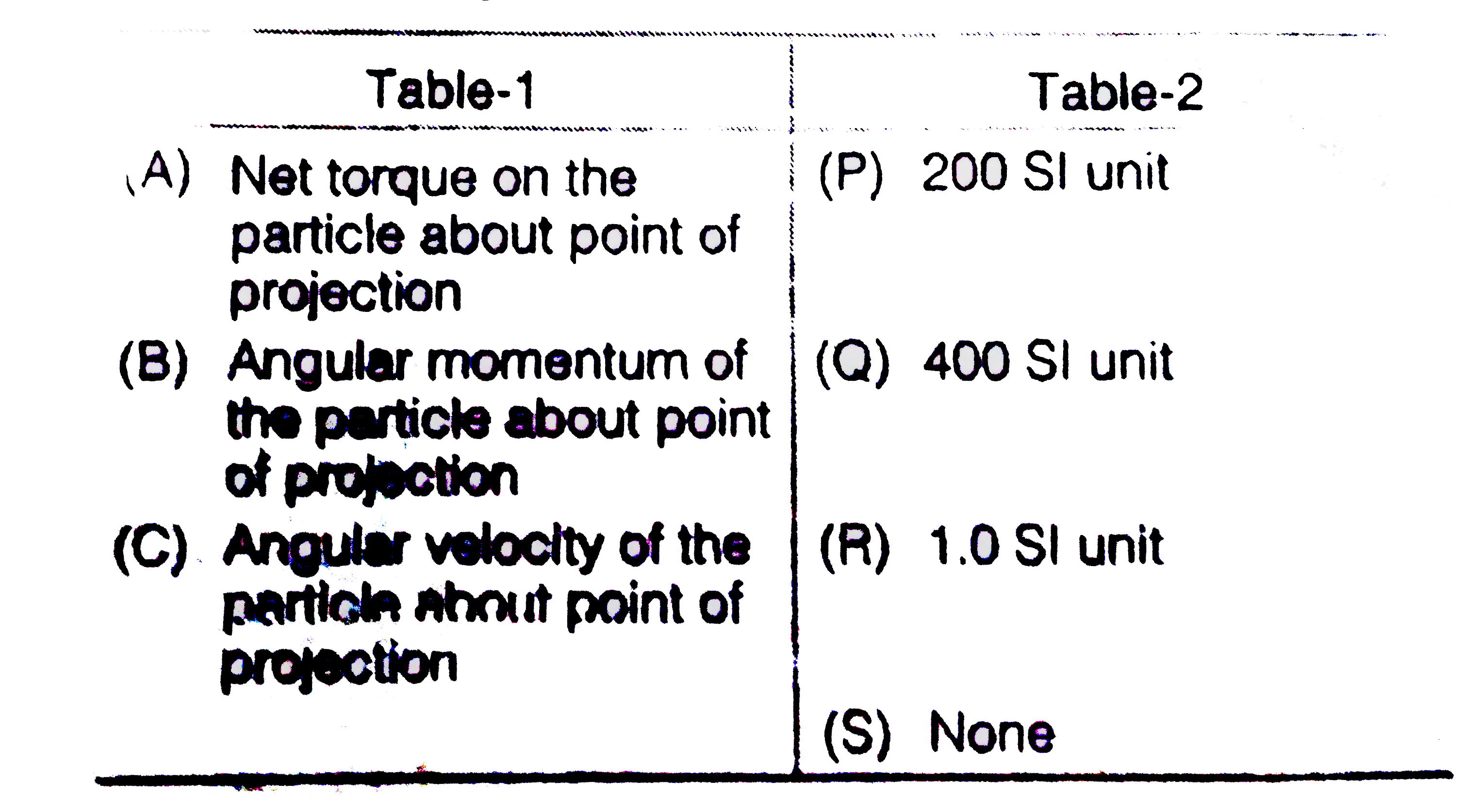
View SolutionA particle of mass m=1kg is projected with speed u=20√2m/s at angle θ=45∘ with horizontal find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle of mass m is projected with a speed v at an angle θ with the horizontal. Find the angular momentum of the particle about an axis passing through point of projection and perpendicular to the plane of motion of the particle.
(a) When the particle is at maximum height and
(b) When the particle is just about to collide with the horizontal surface
View SolutionA stone is projected from the ground with a velocity of 20 m/s at angle 30∘ with the horizontal. After one second it clears a wall then find height of the wall. (g=10ms−2)
View SolutionA ball is projected from the point O with velocity 20 m/s at an angle of 60∘ with horizontal as shown in figure. At highest point of its trajectory it strikes a smooth plane of inclination 30∘ at point A. The collision is perfectly inelastic. The maximum height from the ground attained by the ball is (g=10m/s2)

View SolutionA small ball is projected at an angle α with an initial velocity u between two vertical walls such that in the absence of the wall its range would have been 5d. Given that all the collisions are perfectly elastic and distance between the walls be d2, find.
(a) maximum height atained by the ball.
(b) total number of collisions with the walls before the ball comes back to the ground, and
(c) point at which the ball finally falls. The walls are supposed to be very tall.

View SolutionA particle is projected from ground with velocity 20(√2)m/s at 45∘. At what time particle is at height 15 m from ground? (g=10m/s2)
View SolutionAn electric field is acting vertically upwards . A particle of mass 1 mg and charge −1μC is projected with a velocity 20m/s at an angle 45∘ with the horizontal . Its horizontal range is 10 m, then the intensity of electric field is (g=10m/s2)
View Solution

