Two particles A and B of equal masses lie close together on a horizontal table and are connected by a light inextensible string of length l. A is projected vertically upwards with a velocity √10gl. Find the velocity with which it reaches the table again.
The correct Answer is:B
To solve the problem, let's break it down step by step:
Step 1: Understand the System
We have two particles A and B of equal mass connected by a light inextensible string of length l. Particle A is projected vertically upwards with an initial velocity of √10gl.
Step 2: Determine the Height at Which the String Becomes Tight
As particle A moves upward, it will rise until the string connecting it to particle B becomes taut. This occurs when particle A has moved a distance l upwards.
Step 3: Calculate the Velocity of A When the String Becomes Tight
Using the kinematic equation:
v2=u2+2as
where:
- u=√10gl (initial velocity)
- a=−g (acceleration due to gravity, negative because it is acting downwards)
- s=l (distance moved upwards)
Substituting these values into the equation:
v21=(√10gl)2−2g(l)
v21=10gl−2gl=8gl
Thus, the velocity v1 of particle A when the string becomes taut is:
v1=√8gl
Step 4: Apply Conservation of Momentum
When the string becomes taut, both particles A and B will move together. Let v2 be the common velocity of both particles just after the string becomes tight. By the conservation of momentum:
mA⋅v1=(mA+mB)⋅v2
Since the masses are equal, we can simplify:
m⋅√8gl=2m⋅v2
v2=√8gl2=√82√gl=√2gl
Step 5: Determine the Final Velocity When A Reaches the Table
As both particles A and B fall back to the table, they will have the same final speed when they reach the table. We can use the kinematic equation again to find this final speed.
Using the equation:
v2=u2+2as
where:
- u=v2=√2gl (initial velocity just after the string becomes taut)
- a=g (acceleration due to gravity)
- s=l (distance fallen)
Substituting these values:
v2=(√2gl)2+2g(l)
v2=2gl+2gl=4gl
Thus, the final velocity v when particle A reaches the table is:
v=√4gl=2√gl
Final Answer
The velocity with which particle A reaches the table again is 2√gl.
---
We have two particles A and B of equal mass connected by a light inextensible string of length l. Particle A is projected vertically upwards with an initial velocity of √10gl.
As particle A moves upward, it will rise until the string connecting it to particle B becomes taut. This occurs when particle A has moved a distance l upwards.
Using the kinematic equation:
v2=u2+2as
where:
- u=√10gl (initial velocity)
- a=−g (acceleration due to gravity, negative because it is acting downwards)
- s=l (distance moved upwards)
v21=(√10gl)2−2g(l)
v21=10gl−2gl=8gl
Thus, the velocity v1 of particle A when the string becomes taut is:
v1=√8gl
When the string becomes taut, both particles A and B will move together. Let v2 be the common velocity of both particles just after the string becomes tight. By the conservation of momentum:
mA⋅v1=(mA+mB)⋅v2
Since the masses are equal, we can simplify:
m⋅√8gl=2m⋅v2
v2=√8gl2=√82√gl=√2gl
As both particles A and B fall back to the table, they will have the same final speed when they reach the table. We can use the kinematic equation again to find this final speed.
v2=u2+2as
where:
- u=v2=√2gl (initial velocity just after the string becomes taut)
- a=g (acceleration due to gravity)
- s=l (distance fallen)
v2=(√2gl)2+2g(l)
v2=2gl+2gl=4gl
Thus, the final velocity v when particle A reaches the table is:
v=√4gl=2√gl
The velocity with which particle A reaches the table again is 2√gl.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Comprehension Based Questions
Explore 3 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
Similar Questions
A particle is projected vertically upwards with a velocity of 20m/sec. Find the time at which distance travelled is twice the displacement
View SolutionA particle is projected vertically upwards from ground with velocity 10 m/s. Find the time taken by it to reach at the highest point ?
View SolutionTwo bodies of same mass tied with an inelastic string of length l lie together. One of them is projected vertically upwards with velocity √6gl. Find the maximum height up to which the centre of mass system of the two masses rises.
View SolutionA particle suspended by a light inextensible thread of length l is projected horizontally from its lowest position with velocity √7gl/2. The string will slack after swinging through an angle equal to
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizonally with speed √gl . Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.
View SolutionA particle suspended from a fixed point, by a light inextensible thread of length L is projected horizontally from its lowest position with velocity 7gL . The thread will slack after swinging through an angle , such that equal
View SolutionA body is hanging from a rigid support. by an inextensible string of length '1' . It is struck inelastically by an identical body of mass in with horizontal velocity v=√2gl the tension in the string increases just after the striking by
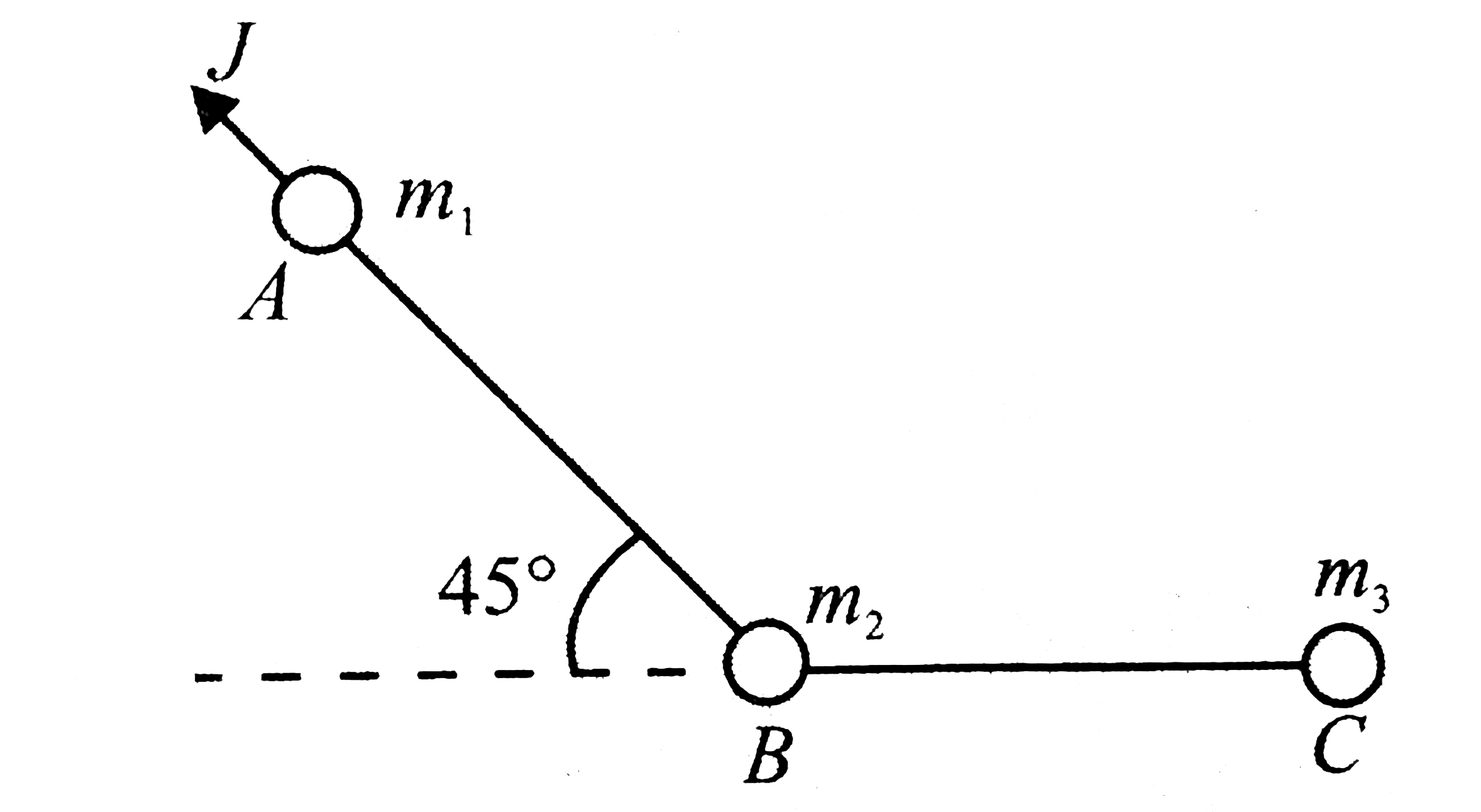
View SolutionThree particles A,B and C of respective masses m1,m2 and m3 lie on a smooth horizontal surface, and an fastened to two light inextensible strings as shown in Fig. The particle A is imparted an impulse J along −−→BA . Find the initial speed of each particle.
View SolutionA bob of mass m suspended by a light inextensible string of length 'l' from a fixed point. The bob is given a speed of √6gl. Find the tension in the string when string deflects through an angle 120∘ from the vertical.
View SolutionTwo identical particles A and B of mass m each are connected together by a light and inextensible string of length l. The particle are held at rest in air in same horizontal level at a separation I. Both particles are released simultaneously and one of them (say A) is given speed V0 vertically upward. Choose the correct options (s). Ignore air resistance.
View Solution

