A gun of mass M(including the carriage) fires a shot of mass m. The gun along with the carriage is kept on a smooth horizontal surface. The muzzle speed of the bullet vr is constant. Find
(a) The elevation of the gun with horizontal at which maximum range of bullet with respect to the ground is obtained.
(b) The maximum range of the bullet.
The correct Answer is:A, B, D
To solve the problem, we will break it down into two parts: finding the elevation angle for maximum range and calculating the maximum range itself.
Part (a): Finding the elevation angle for maximum range
1. Understanding the System:
- We have a gun of mass M (including the carriage) that fires a bullet of mass m.
- The bullet has a muzzle speed vr and is fired at an angle θ with respect to the horizontal.
2. Initial Conditions:
- Before firing, the entire system (gun + bullet) is at rest. Therefore, the initial momentum of the system is zero.
3. Applying Conservation of Momentum:
- When the bullet is fired, the gun recoils. By conservation of momentum:
0=mv+MVg
where v is the velocity of the bullet and Vg is the velocity of the gun after firing.
- The velocity of the bullet can be expressed as:
v=vrcosθ+Vg
4. Finding the Velocity of the Gun:
- Rearranging the momentum equation gives:
Vg=−mvrcosθM
5. Velocity of the Bullet:
- Substituting Vg back into the bullet's velocity equation:
v=vrcosθ−mvrcosθM
- Simplifying gives:
v=vrcosθ(1−mM)
6. Time of Flight:
- The time of flight T for the bullet can be calculated using the vertical component of the bullet's velocity:
T=2vrsinθg
7. Finding the Elevation Angle for Maximum Range:
- The horizontal range R is given by:
R=VgT
- Substituting Vg and T:
R=−mvrcosθM⋅2vrsinθg
- To maximize R, we need to maximize sin2θ. This occurs at θ=45∘.
Part (b): Calculating the Maximum Range
1. Substituting θ=45∘:
- At θ=45∘, sin2θ=1.
- The range becomes:
R=mv2rg(M+m)
2. Final Expression for Maximum Range:
- Thus, the maximum range R of the bullet is:
R=mv2rg(M+m)
Summary of Results:
- (a) The elevation angle θ for maximum range is 45∘.
- (b) The maximum range of the bullet is R=mv2rg(M+m).
- We have a gun of mass M (including the carriage) that fires a bullet of mass m.
- The bullet has a muzzle speed vr and is fired at an angle θ with respect to the horizontal.
- Before firing, the entire system (gun + bullet) is at rest. Therefore, the initial momentum of the system is zero.
- When the bullet is fired, the gun recoils. By conservation of momentum:
0=mv+MVg
where v is the velocity of the bullet and Vg is the velocity of the gun after firing.
- The velocity of the bullet can be expressed as:
v=vrcosθ+Vg
- Rearranging the momentum equation gives:
Vg=−mvrcosθM
- Substituting Vg back into the bullet's velocity equation:
v=vrcosθ−mvrcosθM
- Simplifying gives:
v=vrcosθ(1−mM)
- The time of flight T for the bullet can be calculated using the vertical component of the bullet's velocity:
T=2vrsinθg
- The horizontal range R is given by:
R=VgT
- Substituting Vg and T:
R=−mvrcosθM⋅2vrsinθg
- To maximize R, we need to maximize sin2θ. This occurs at θ=45∘.
- At θ=45∘, sin2θ=1.
- The range becomes:
R=mv2rg(M+m)
- Thus, the maximum range R of the bullet is:
R=mv2rg(M+m)
- (a) The elevation angle θ for maximum range is 45∘.
- (b) The maximum range of the bullet is R=mv2rg(M+m).
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Comprehension Based Questions
Explore 3 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
Similar Questions
A bullet of mass m leaves a gun of mass M kept on a smooth horizontal surface . If the speed of the bullet relative to the gun is v , the magnitude of recoil speed of the gun will be
View SolutionThe maximum range of a rifle bullet on the horizontal ground is 6km. Find its maximum range on an inclined of 30∘.
View Solution
Knowledge Check
A gun fires two bullets at 60∘ and 30∘ with horizontal. The bullets strike at same horizontal distance. The ratio of the maximum height for the two bullets is in the ratio
A2:1B3:1C4:1D1:1
If the range of a gun which fires a shell with muzzle speed V is R , then the angle of elevation of the gun is
View SolutionIf the range of a gun which fires a shell with muzzle speed V is R , then the angle of elevation of the gun is
View SolutionA bullet of mass m embeds itself in a block of mass M resting on a smooth horizontal surface, attached to a spring of force constant k. If the initial speed of the bullet is v0 along horizontal, find (a) the maximum compression of the spring and (b) the time for the bullet - block system to come to rest.
View SolutionA gun of mass M fires a bullet of mass m with a Kinetic energy E. The velocity of recoil of the gun is
View SolutionTwo blocks A and B of masses m and 2m are placed on a smooth horizontal surface. Block B is given a speed of 3m/s. Find
(i) The maximum speed of A
(ii) The minimum speed of B.
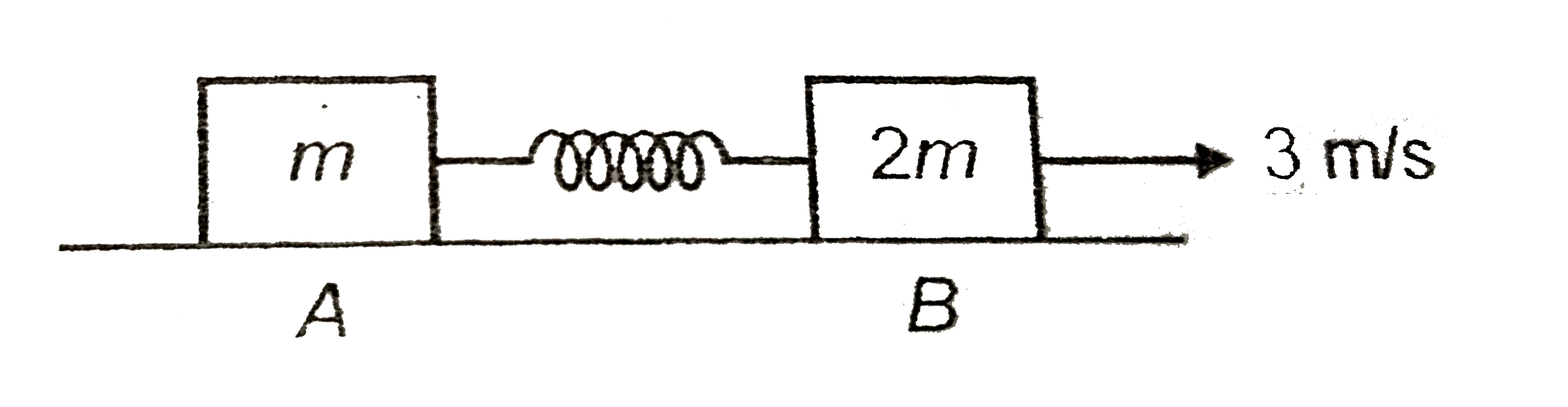
View SolutionA gun is firing bullets with velocity v0 by rotating it through 360∘ in the horizontal plane. The maximum area covered by the bullets is
View SolutionA gun of mass M fires a bullet of mass m, with a Kinetic energy E. The total kinetic energy in the firing process is
View Solution

