A shell of mass 1kg is projected with velocity 20m/s at an angle 60∘ with horizontal. It collides inelastically with a ball of mass 1kg which is suspended through a thread of length 1m. The other end of the thread is attached to the ceiling of a trolley of mass 43kg as shown in figure. Initially the trolley is stationary and it is free to move along horizontal rails wihtout any friction. What is the maximum deflection of the thread with vertical? String does not slack. Take g=10m/s2.

H=u2sin2θ2g=(20)2×342×10=15m
i.e. the shell strikes the ball at highest point of its trajectory. Velocity of (ball+shell) just after collision,
v=ucos60∘2
(from consevation of linear momentum)
=202×2=5m/s

At highest point combined mass is at rest relative to the trolley. Let v be the velocity of trolley at this instant. From conservation of linear momentum we have,
2×5=(2+43)v or v=3m/s
From conservation of energy, we have
12×2×(5)2−12(2+43)(3)2=2×10(1−cosθ)
Solving we get, cosθ=12
∴θ=60∘
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Comprehension Based Questions
Explore 3 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
Similar Questions
A ball of mass in m=1kg is hung vertically by a thread of length l=1.50m. Upper end of the thread is attached to the ceiling of a trolley of mass M=4kg. Initially, the trolley is stationary and it is free to move along horizontal rails without friction. A shell of mass m=1 kg, moving horizontally with velocity v0=6m/s collides with the ball and gets stuck with it. As a result, the thread starts to deflect towards right.
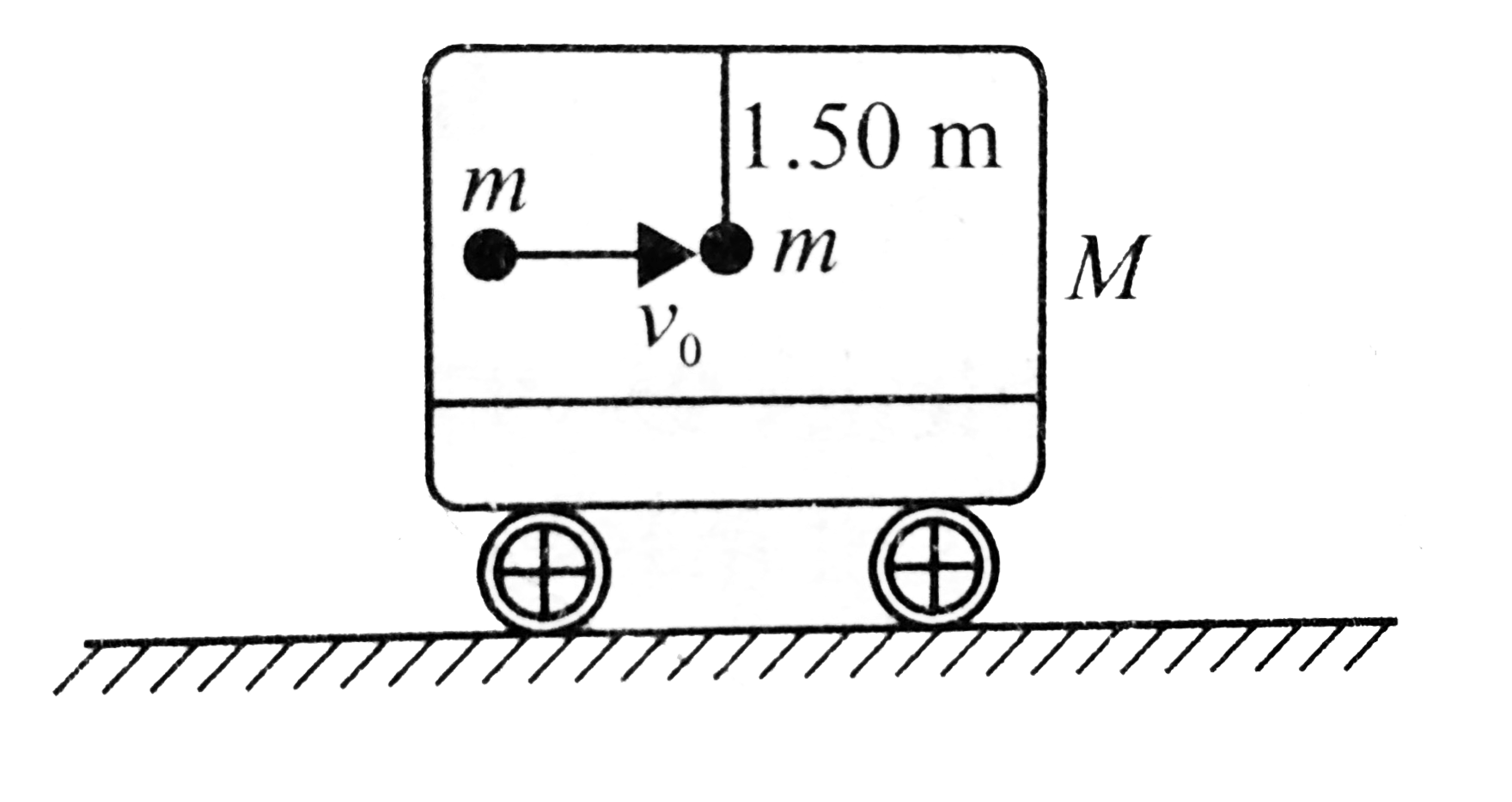
The velocity of the combined body just after collision is
View SolutionA ball of mass in m=1kg is hung vertically by a thread of length l=1.50m. Upper end of the thread is attached to the ceiling of a trolley of mass M=4kg. Initially, the trolley is stationary and it is free to move along horizontal rails without friction. A shell of mass m=1kg, moving horizontally with velocity v0=6m/s collides with the ball and gets stuck with it. As a result, the thread starts to deflect towards right.

At the time of maximum deflection of the thread with vertical, the trolley will move with velocity
View SolutionA ball of mass 0.2 kg moves with a velocity of 20m/sec and it stops in 0.1 sec , then the force on the ball is
View SolutionA ball of mass 0.2 kg moves with a velocity of 20m/sec and it stops in 0.1 sec , then the force on the ball is
View SolutionA ball of mass 2kg is thrown with velocity 10ms at an angle of 30°to the horizontal and another ball with the same mass is thrown at an angel of 60° to the horizontal with the same speed.The ratio will be their range will be
View SolutionA ball of mass 1kg moving with 4m−1 along +x-axis collides elastically with an another ball of mass 2kg moving with 6m/s is opposite direction. Find their velocities after collision.
View SolutionA ball of mass 2 kg is projected horizontally with a velocity 20m/s from a building of height 15m. The speed with which body hits the ground is :
View SolutionA block of mass 1kg is tied to a string of length 1m the other end of which is fixed The block is moved on a smooth horizontal table with constant speed 10ms−1. Find the tension in the string
View SolutionIn the arrangements shown in the figure masses of each ball is 1kg and mass of trolley is 4kg. In the figure, shell of mass 1kg moving horizontally with velocity v=6ms−1 collides with the ball and get stuck to it then its maximum deflection of the thread (length 1.5m) with vertical

View SolutionA mass of 2kg is suspended with thread AB (figure) Thread CD of the same type is attached to the other end of 2kg mass. Lower thread is pulled gradually, harder and harder in the downward direction so as to apply force on AB. which of the threads will break and why?
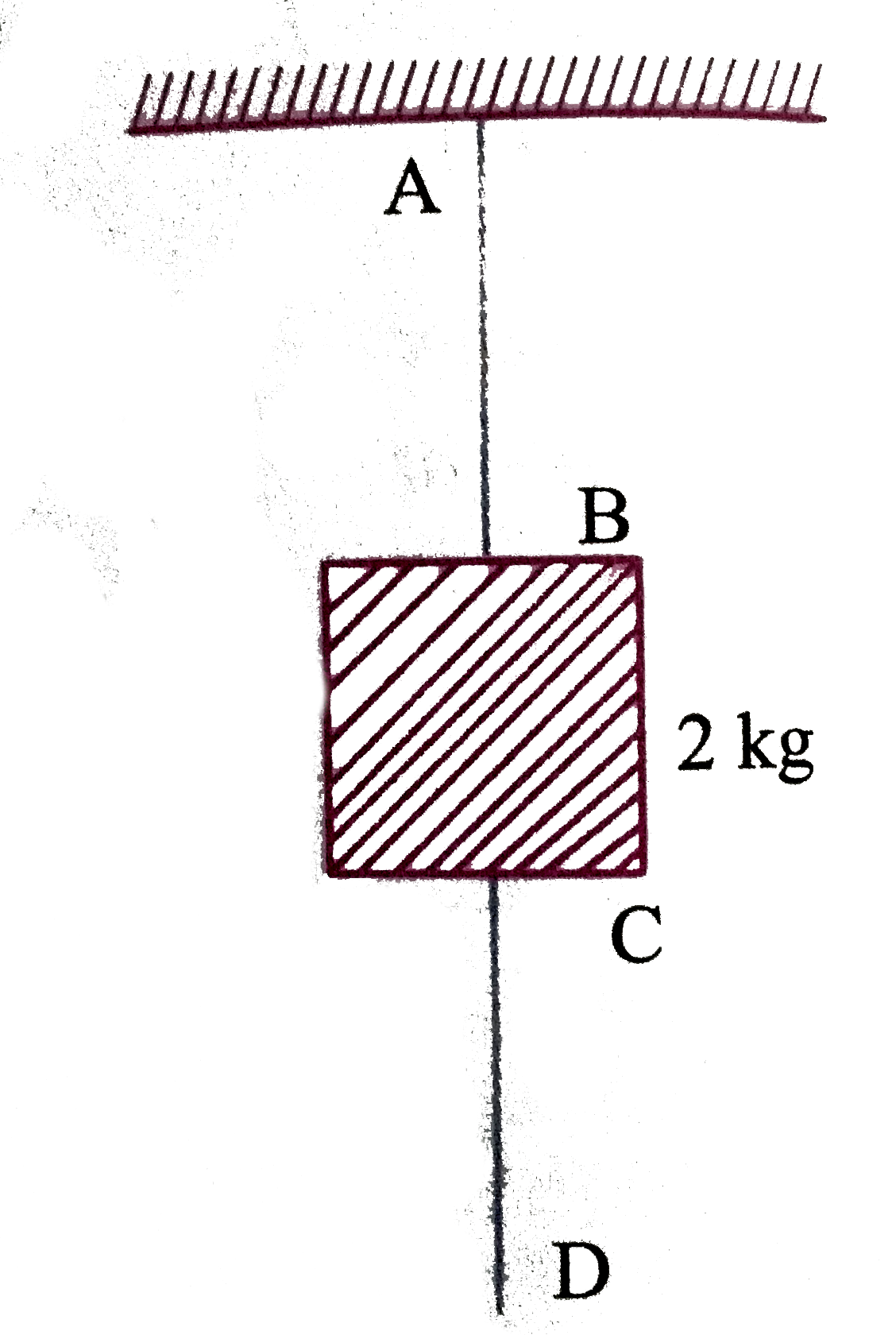
View Solution

