A ball of mass 2 kg is projected horizontally with a velocity 20m/s from a building of height 15m. The speed with which body hits the ground is :
20 m/s
10(7)1/2m/s
25 m/s
35 m/s
The correct Answer is:B
To find the speed with which the ball hits the ground, we need to consider both the horizontal and vertical components of the ball's motion. Here are the steps to solve the problem:
Step 1: Identify the given data
- Mass of the ball (m) = 2 kg (not needed for speed calculation)
- Initial horizontal velocity (u_x) = 20 m/s
- Height of the building (h) = 15 m
- Acceleration due to gravity (g) = 10 m/s²
Step 2: Calculate the time of flight
The time it takes for the ball to fall to the ground can be calculated using the formula for free fall:
h=12gt2
Rearranging for t:
t=√2hg
Substituting the values:
t=√2×15m10m/s2=√3≈1.73s
Step 3: Calculate the vertical velocity just before impact
The vertical velocity (vy) just before hitting the ground can be calculated using the equation:
vy=gt
Substituting the values:
vy=10m/s2×1.73s≈17.3m/s
Step 4: Calculate the resultant velocity just before impact
The resultant velocity (v) of the ball just before it hits the ground can be found using the Pythagorean theorem, since the horizontal and vertical components are perpendicular:
v=√u2x+v2y
Substituting the values:
v=√(20m/s)2+(17.3m/s)2
Calculating:
v=√400+299.29≈√699.29≈26.4m/s
Final Answer
The speed with which the body hits the ground is approximately 26.4 m/s.
---
- Mass of the ball (m) = 2 kg (not needed for speed calculation)
- Initial horizontal velocity (u_x) = 20 m/s
- Height of the building (h) = 15 m
- Acceleration due to gravity (g) = 10 m/s²
The time it takes for the ball to fall to the ground can be calculated using the formula for free fall:
h=12gt2
Rearranging for t:
t=√2hg
Substituting the values:
t=√2×15m10m/s2=√3≈1.73s
The vertical velocity (vy) just before hitting the ground can be calculated using the equation:
vy=gt
Substituting the values:
vy=10m/s2×1.73s≈17.3m/s
The resultant velocity (v) of the ball just before it hits the ground can be found using the Pythagorean theorem, since the horizontal and vertical components are perpendicular:
v=√u2x+v2y
Substituting the values:
v=√(20m/s)2+(17.3m/s)2
Calculating:
v=√400+299.29≈√699.29≈26.4m/s
The speed with which the body hits the ground is approximately 26.4 m/s.
Topper's Solved these Questions
- WORK ENERGY AND POWER Book:VMC MODULES ENGLISHChapter:WORK ENERGY AND POWER Exercise:ENABLE
Explore 50 Videos
- WORK ENERGY AND POWER Book:VMC MODULES ENGLISHChapter:WORK ENERGY AND POWER Exercise:EFFICIENT
Explore 50 Videos
- WAVE MOTIONBook:VMC MODULES ENGLISHChapter:WAVE MOTIONExercise:JEE ADVANCED ARCHIVE LEVEL 2 (TRUE FALSE TYPE)
Explore 4 Videos
Similar Questions
A ball is projected horizontally with a velocity of 5ms−1 from the top of a building 19.6m high. How long will the ball take to hit the ground ?
View SolutionA stone is thrown vertically up at 20 m/s from a tower 80 m height. The speed with which it hits the ground is [g=10m/s2]
View SolutionA body of mass m is projected horizontally with a velocity v from the top of a tower of height h and it reaches the ground at a distance x from the foot of the tower. If a second body of mass 2m is projected horizontally from the top of a tower of height 2h, it reaches the ground at a distance 2x from the foot of the tower. The horizontal veloctiy of the second body is.
View SolutionA body is thrown horizontally with a velocity of v m/s from the top of a tower of height 2h reaches the ground in 't' seconds. If another body double the mass is thrown horizontally with a velocity 5v m/s from the top of another tower of height 8h it reaches the ground in a time of
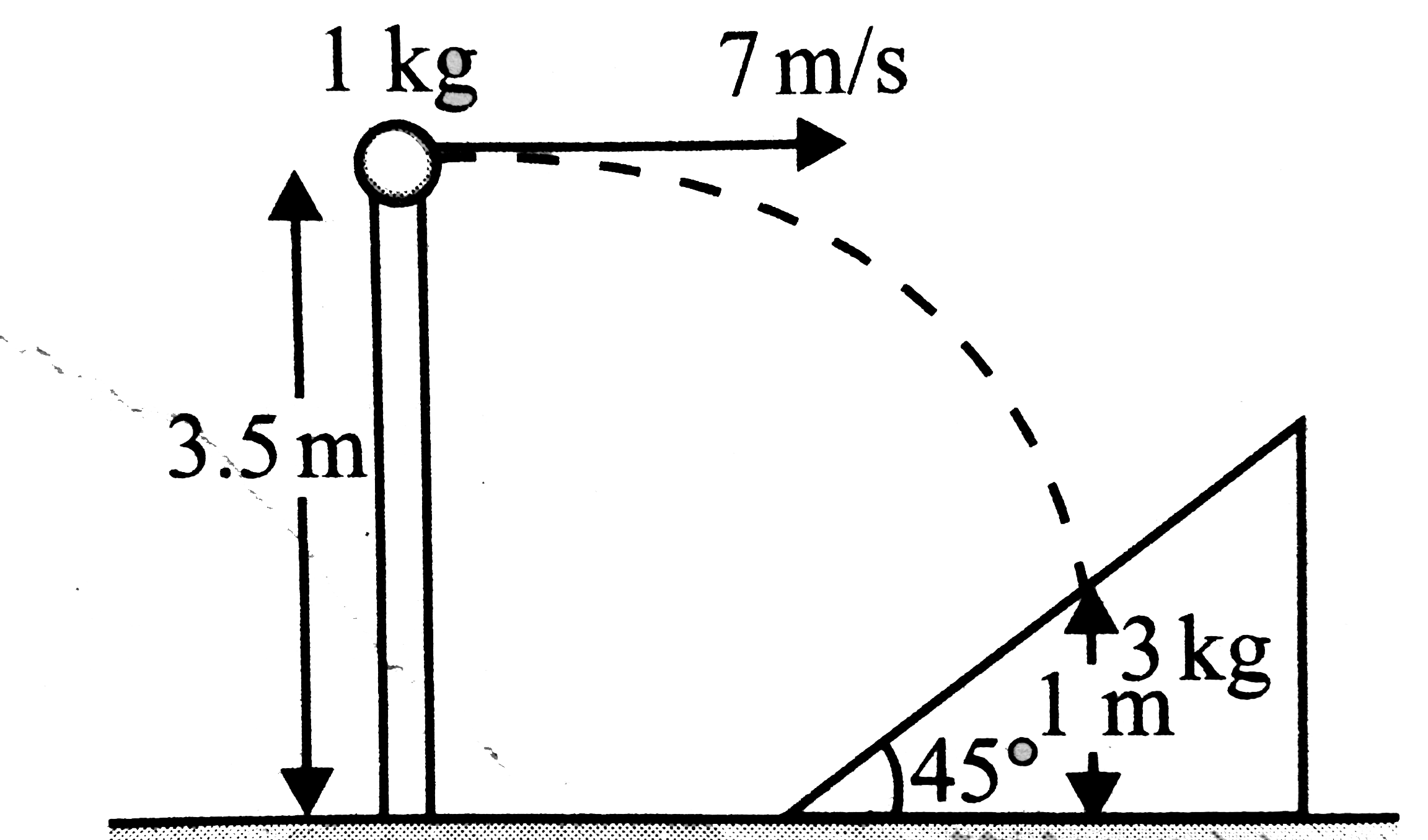
View SolutionA smooth ball of mass 1kg is projected with velocity 7m/s horizontal from a tower of height 3.5m. It collides elastically with a wedge of mass 3 kg and inclination of 45∘ kept on ground. The ball collides with the wedge at a height of 1m above the ground. Find the velocity of the wedge and the ball after collision. (Neglect friction at any contact.)
View SolutionA boy throws a ball with a velocity of 15 m/s at an angle of 15° with the horizontal. The distance at which the ball strikes the ground is
View SolutionA body of mass 2kg is projected from the ground with a velocity 20ms−1 at an angle 30∘ with the vertical. If t1 is the time in seconds at which the body is projected and t2 is the time in seconds at which it reaches the ground, the change in momentum in kgms−1 during the time (t2−t1) is
View SolutionA ball is projected horizontally from the top of a building 19.6 m high. If the line joining the point of projection to the point where it hits the ground makes an angle of 45∘ to the horizontal, the initial velocity of the ball is
View SolutionA particle of mass 50 g is projected horizontally from the top of a tower of height 50 m with a velocity 20m/s. If g=10m/s2, then find the :-
View SolutionA particle of mass m is projected at an angle of 60∘ with a velocity of 20m/s relative to the ground from a plank of same mass m which is placed on smooth surface Initially Plank was at rest The minimum length of the plank for which the ball will fall on the plank itself is (g=10m/s2)

View Solution

