A force F1 acts on a particle so as to accelerate it from rest to a velocity v. The force F1 is then replaced by F2 which decelerates it to rest
(a)F1is always equal to F2
(b)F2is greater than F1
(c)F2 may be smaller than, greater than or equal to F1
(d)F2 cannot be equal to F1
The correct Answer is:C
To solve the problem, we need to analyze the forces acting on a particle as it accelerates and then decelerates.
1. Understanding the Initial Condition:
- The particle starts from rest, which means its initial velocity u=0.
- A force F1 is applied to the particle, causing it to accelerate to a velocity v.
2. Applying Newton's Second Law:
- According to Newton's second law, the acceleration a1 produced by the force F1 can be expressed as:
F1=m⋅a1
- Here, m is the mass of the particle.
3. Finding the Final Velocity:
- The final velocity v can be related to the acceleration and time using the equation:
v = u + a_1 t \quad \text{(where u = 0 )}
- Thus, we have:
v=a1t
4. Transition to Deceleration:
- After reaching the velocity v, the force F1 is replaced by a force F2 that decelerates the particle to rest.
- This means the final velocity vf=0.
5. Applying Force F2:
- The deceleration a2 caused by the force F2 can be expressed as:
F2=m⋅(−a2)
- The negative sign indicates that the acceleration is in the opposite direction to the motion.
6. Condition for Coming to Rest:
- For the particle to come to rest, the force F2 must be sufficient to overcome the momentum of the particle. Therefore, F2 must be at least equal to or greater than F1:
F2≥F1
7. Analyzing the Options:
- Option A: F1 is always equal to F2 - This is incorrect because F2 can be greater than F1.
- Option B: F2 is greater than F1 - This is a valid condition for deceleration.
- Option C: F2 may be smaller, greater, or equal to F1 - This is incorrect since F2 cannot be smaller than F1.
- Option D: F2 cannot be equal to F1 - This is incorrect because F2 can be equal to F1 and still bring the particle to rest.
Conclusion:
The correct answer is Option B: F2 is greater than F1.
- The particle starts from rest, which means its initial velocity u=0.
- A force F1 is applied to the particle, causing it to accelerate to a velocity v.
- According to Newton's second law, the acceleration a1 produced by the force F1 can be expressed as:
F1=m⋅a1
- Here, m is the mass of the particle.
- The final velocity v can be related to the acceleration and time using the equation:
v = u + a_1 t \quad \text{(where u = 0 )}
- Thus, we have:
v=a1t
- After reaching the velocity v, the force F1 is replaced by a force F2 that decelerates the particle to rest.
- This means the final velocity vf=0.
- The deceleration a2 caused by the force F2 can be expressed as:
F2=m⋅(−a2)
- The negative sign indicates that the acceleration is in the opposite direction to the motion.
- For the particle to come to rest, the force F2 must be sufficient to overcome the momentum of the particle. Therefore, F2 must be at least equal to or greater than F1:
F2≥F1
- Option A: F1 is always equal to F2 - This is incorrect because F2 can be greater than F1.
- Option B: F2 is greater than F1 - This is a valid condition for deceleration.
- Option C: F2 may be smaller, greater, or equal to F1 - This is incorrect since F2 cannot be smaller than F1.
- Option D: F2 cannot be equal to F1 - This is incorrect because F2 can be equal to F1 and still bring the particle to rest.
The correct answer is Option B: F2 is greater than F1.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Objective Question
32 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason
28 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A force P acts on a particle so as to accelerate it from rest to certain velocity. If P is replaced then by Q which decelerates it to rest.
View SolutionA 5kg mass is accelerated from rest to 60 m/s in 1 sec. what force acts on it:
View SolutionA time dependent force F=6t acts on a particle of mass 1kg. If the particle starts from rest, the work done by the force during the first 1sec. will be
View SolutionWhen a force F acts on a particle of mass m, the acceleration of particle becomes a. now if two forces of magnitude 3F and 4F acts on the particle simultaneously as shown in figure, then the acceleration of the particle is
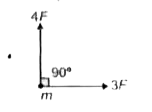
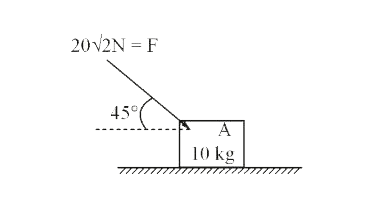
View SolutionA force F acts on a particle kept on a rough surface as shown in the figure. The particle is at rest. Find the net force applied by ground on the particle.
View SolutionForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionA car , starting from rest, accelerates at the rate f through a distance S then continues at constant speed for time t and then decelerates at the rate f2 to come to rest . If the total distance traversed is 15S , then
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
Velocity-time graph of the particle is
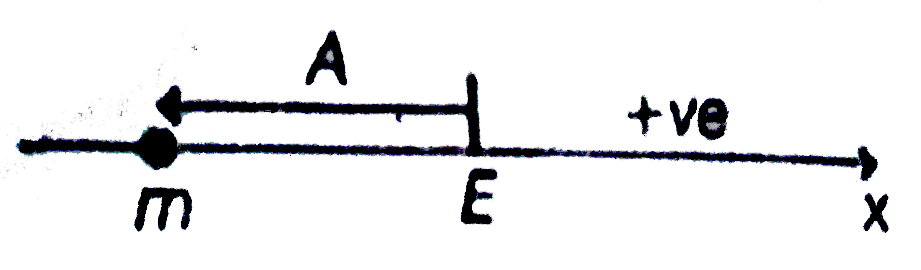
View SolutionAccording to Newton.s second law of motion, resultant force on a particle is in the direction of acceleration of the particle. Two forcce F1andF2 are acting on a particle as shown in the figure. The acceleration of the particle is along X-axis. FInd the value of F1 (in newton)
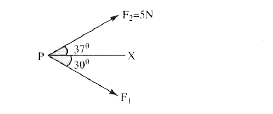
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
What it is the time period of periodic motion of particle.
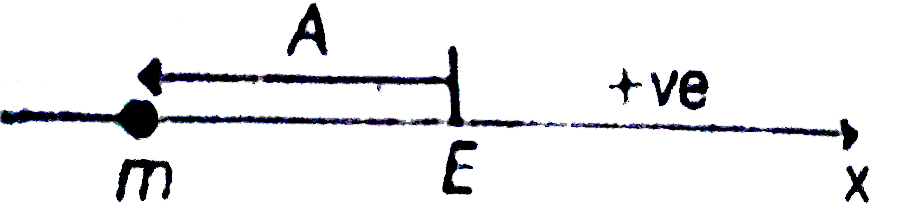
View Solution
