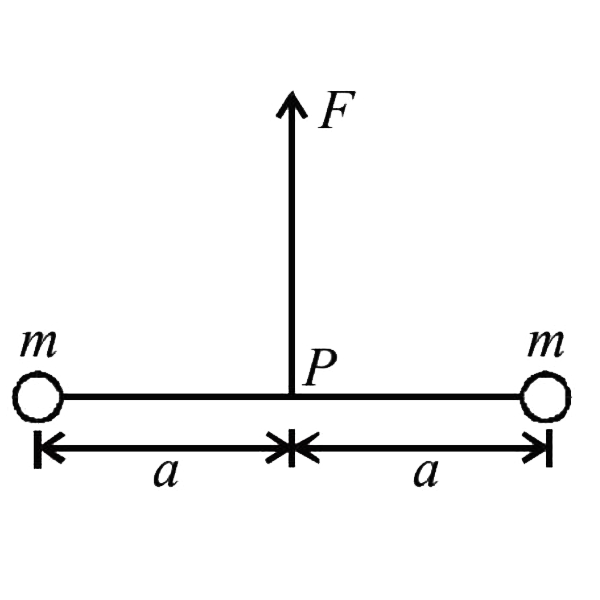
In figure two identical particals each of mass m are tied together with an inextensible string. This is pulled at its centre wwith a constant force F. If the whole system lines on a smooth horizontal plane, then the aceleration of each partical towards each other is
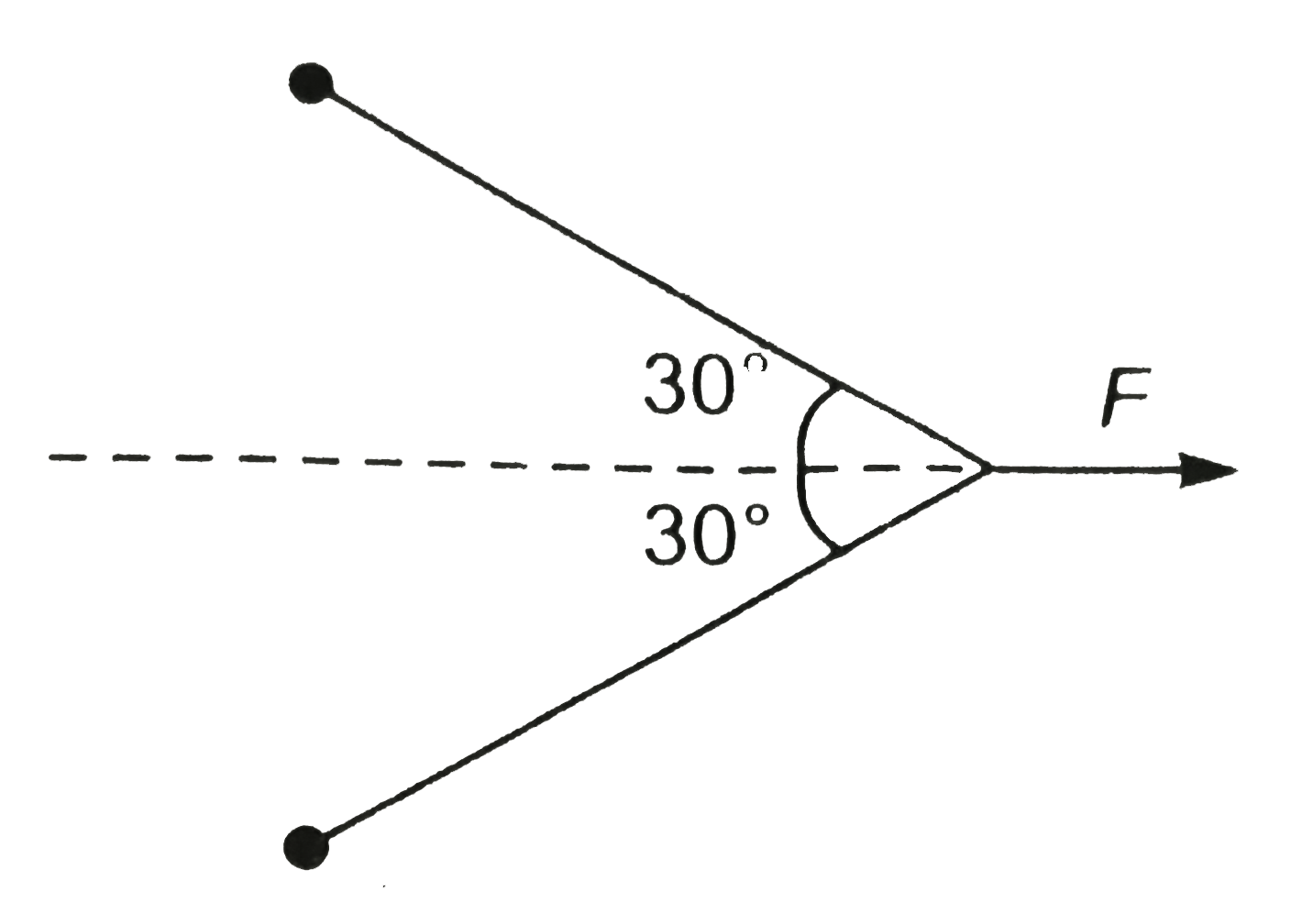
(a)√32Fm
(b)12√3Fm
(c)2√3Fm
(d)√3Fm
The correct Answer is:B
At point P.
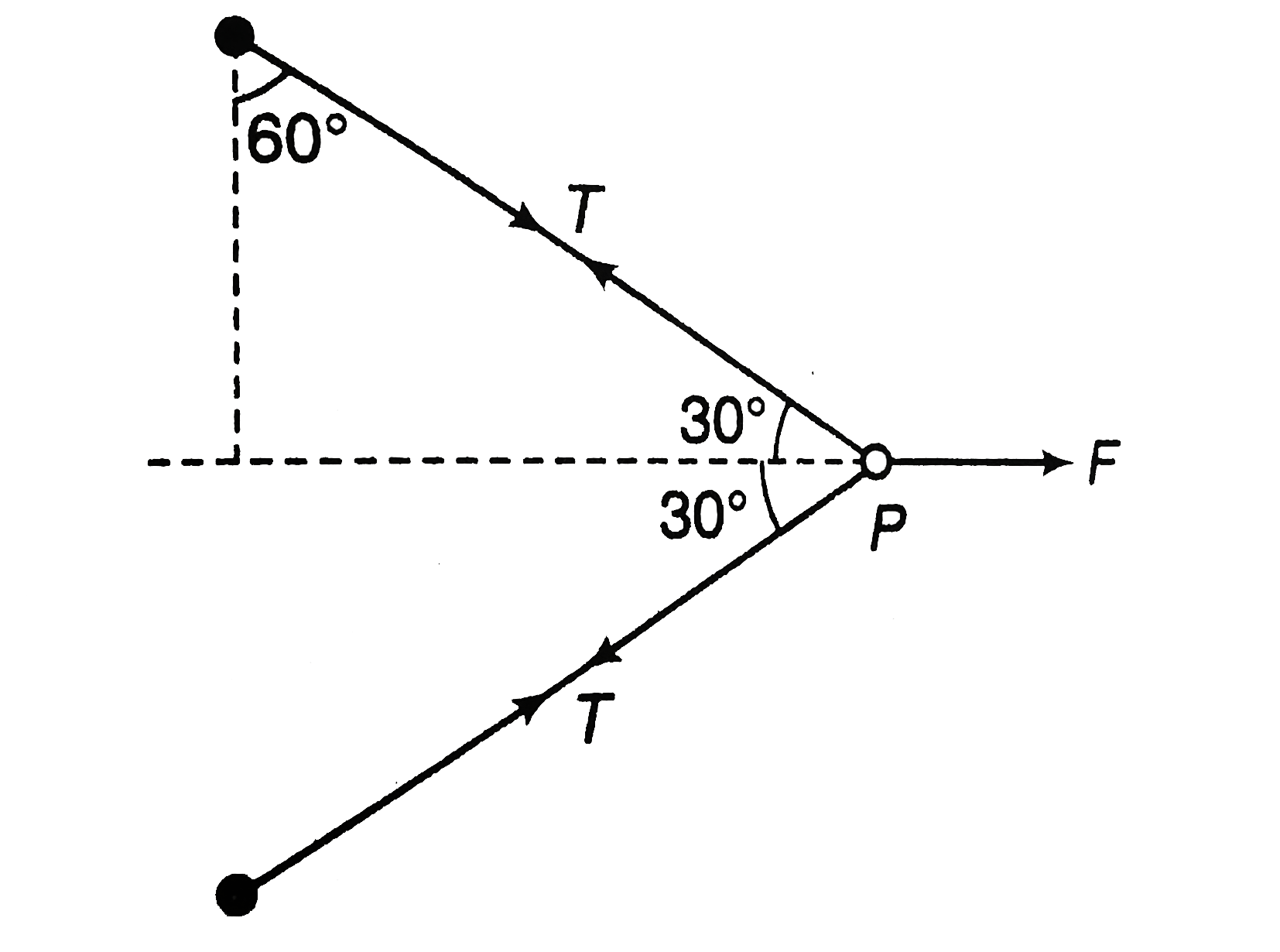
F=2Tcos30∘
T=F√3
Acceleration of partical towards each other
=component of towards each other particalm
=Tcos60∘m=(F/√3)(1/2)m=F2√3m
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Objective Question
32 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason
28 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
Two blocks of equal mass m are tied to each other through light string. One of the blocks is pulled along the line joining them with a constant force F. Find the tension in the string joining the blocks.
View SolutionTwo identical blocks A and B each of mass M are connected to each other through a light string. The system is placed on a smooth horizontal floor. When a constant force F is applied horizontally on the block A, find the tension in the string.
View SolutionTwo particles each of mass m are connected by a light inextensible string and a particle of mass M is attached to the midpoint of the string. The system is at rest on a smooth horizontal table with string just taut and in a straight line. The particle M is given a velocity v along the table perpendicular to the string. Prove that when the two particles are about to collide :
(i) The velocity of M is Mv(M+2m)
(ii) The speed of each of the other particles is (√2M(M+m)(M+2m))v.
View SolutionTwo identical particles move towards each other with velocity 2v and v, respectively. The velocity of the centre of mass is:
View SolutionTwo identical small bodies each of mass m and charge q are suspended from two strings each of length l from a fixed point. This whole system is taken into an orbiting artificial satellite, then find the tensio in strings
View SolutionThree point masses each of mass'm' are joined together using a string to form an equilateral triangle of side 'a'. The system is placed on a smooth horizontal surface and rotated with a constant angular velocity 'ω' about a vertical axis passing through the centroid. Then the tension in each string is
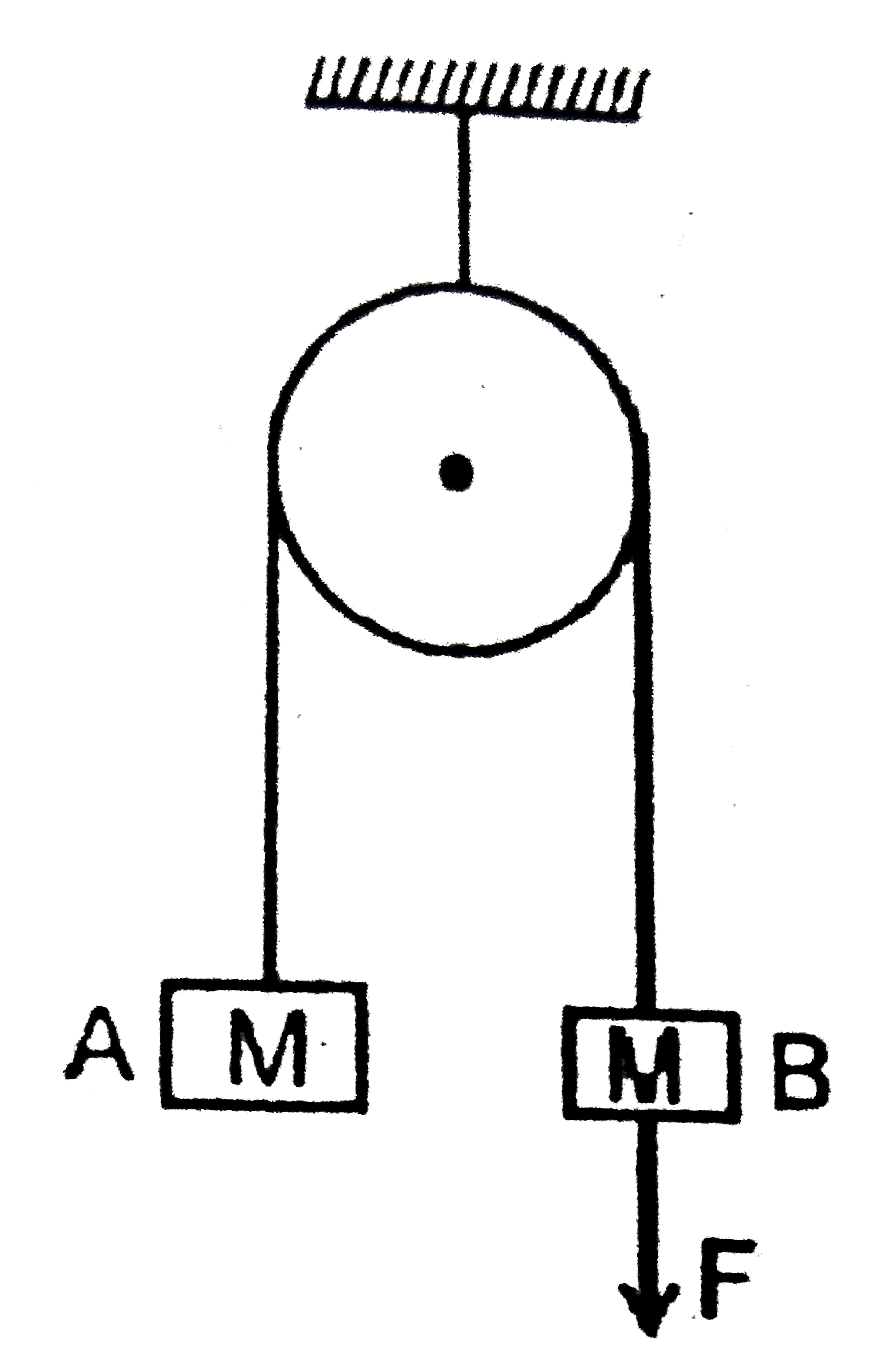
View SolutionTwo particles A and B having equal mass are interconnected by a light inextensible string that passes over a smooth pulley. One of the amsses is pulled downward by a constant force 'F' as shown in diagram, then find the acceleration of the centre of mass of the system (A+B).
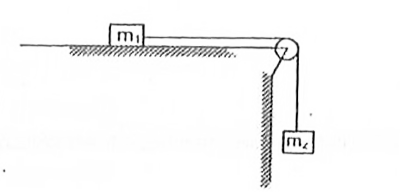
View SolutionA block of mass m1=2 kg is kept on a smooth horizontal table. Another block of mass m2=1 kg is connected to m1 by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
View SolutionThree identical particles A, B and C of mass m lie on a smooth horizontal table. Light inextensible strings which are just taut connect AB and BC and ∠ABC is 135° . An impulse J is imparted to the particle C in the direction BC. Mass of each particle is m. Choose the correct options.

View SolutionTwo particles of mass m each are tied at the ends of a light string of length 2a. The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance a from the centre P (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force F. As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2x, is
View Solution
