Two particle start together from a point O and slide down along straight smooth wire inclined at 30∘ and 60∘ to the vertical plane and on the same slide of vertical through O . The relative acceleration of second with respect to first will be of magnitude
(a)g2
(b)√3g2
(c)g√3
(d)g
The correct Answer is:A
To solve the problem of finding the relative acceleration of the second particle with respect to the first, we will follow these steps:
Step 1: Identify the angles and the gravitational acceleration components
- We have two particles sliding down two different inclined wires. The first particle is on a wire inclined at 30∘ to the vertical, and the second particle is on a wire inclined at 60∘ to the vertical.
- The gravitational acceleration acting on both particles is g.
Step 2: Calculate the acceleration of each particle
- For the first particle (Particle 1) inclined at 30∘:
A1=g⋅cos(30∘)=g⋅√32
- For the second particle (Particle 2) inclined at 60∘:
A2=g⋅cos(60∘)=g⋅12
Step 3: Use the formula for relative acceleration
- The relative acceleration of Particle 2 with respect to Particle 1 is given by:
A21=A2−A1
Step 4: Substitute the values of A1 and A2
- Now substituting the values we calculated:
A21=(g⋅12)−(g⋅√32)
- This simplifies to:
A21=g(12−√32)=g⋅1−√32
Step 5: Calculate the magnitude of the relative acceleration
- The magnitude of the relative acceleration can be calculated using the Pythagorean theorem since the two accelerations are acting at an angle:
|A21|=√A21+A22−2A1A2cos(θ)
- Here, θ is the angle between the two acceleration vectors, which is 30∘ (the difference between 60∘ and 30∘).
Step 6: Substitute the values into the formula
- Substituting the values:
|A21|=
⎷(g⋅√32)2+(g⋅12)2−2(g⋅√32)(g⋅12)cos(30∘)
- This becomes:
|A21|=√3g24+g24−2⋅√3g24⋅12⋅√32
- Simplifying further:
|A21|=√3g24+g24−3g28
- Combine the terms:
|A21|=√4g24−3g28=√g2−3g28=√8g28−3g28=√5g28=g√58
Final Result
The magnitude of the relative acceleration of the second particle with respect to the first is:
|A21|=g√52√2=g√104
- We have two particles sliding down two different inclined wires. The first particle is on a wire inclined at 30∘ to the vertical, and the second particle is on a wire inclined at 60∘ to the vertical.
- The gravitational acceleration acting on both particles is g.
- For the first particle (Particle 1) inclined at 30∘:
A1=g⋅cos(30∘)=g⋅√32
- For the second particle (Particle 2) inclined at 60∘:
A2=g⋅cos(60∘)=g⋅12
- The relative acceleration of Particle 2 with respect to Particle 1 is given by:
A21=A2−A1
- Now substituting the values we calculated:
A21=(g⋅12)−(g⋅√32)
- This simplifies to:
A21=g(12−√32)=g⋅1−√32
- The magnitude of the relative acceleration can be calculated using the Pythagorean theorem since the two accelerations are acting at an angle:
|A21|=√A21+A22−2A1A2cos(θ)
- Here, θ is the angle between the two acceleration vectors, which is 30∘ (the difference between 60∘ and 30∘).
Step 6: Substitute the values into the formula
- Substituting the values:
|A21|=
⎷(g⋅√32)2+(g⋅12)2−2(g⋅√32)(g⋅12)cos(30∘)
- This becomes:
|A21|=√3g24+g24−2⋅√3g24⋅12⋅√32
- Simplifying further:
|A21|=√3g24+g24−3g28
- Combine the terms:
|A21|=√4g24−3g28=√g2−3g28=√8g28−3g28=√5g28=g√58
The magnitude of the relative acceleration of the second particle with respect to the first is:
|A21|=g√52√2=g√104
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Objective Question
32 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason
28 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
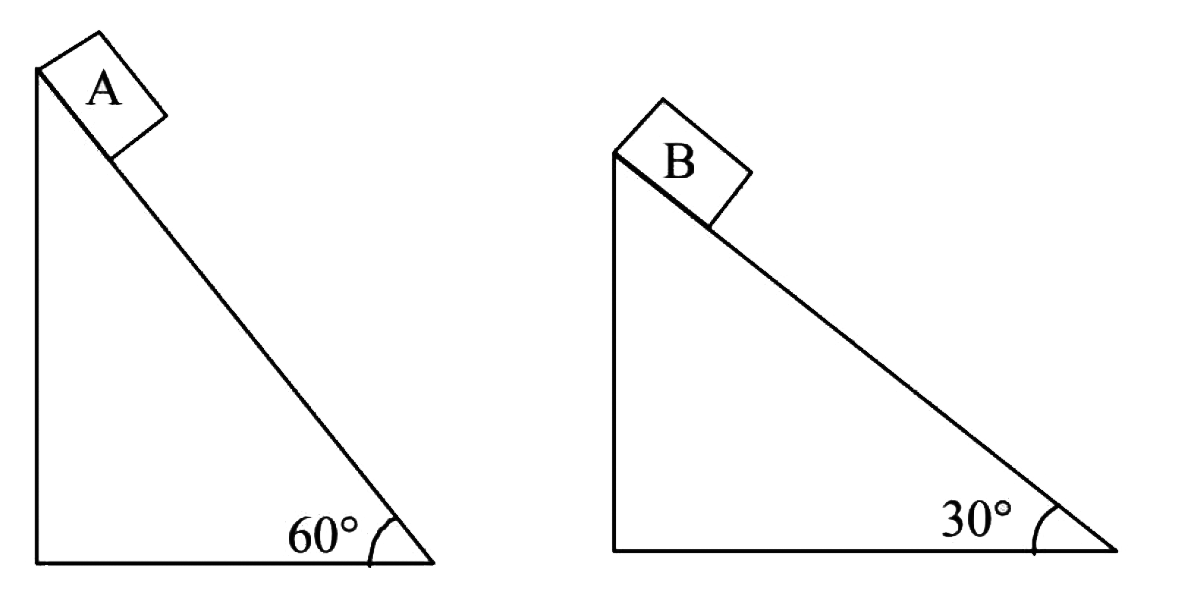
Two fixed frictionless inclined plane making an angle 30∘ and 60∘ with the vertical are shown in the figure. Two block A and B are placed on the two planes. What is the relative vertical acceleration of A with respect to B?
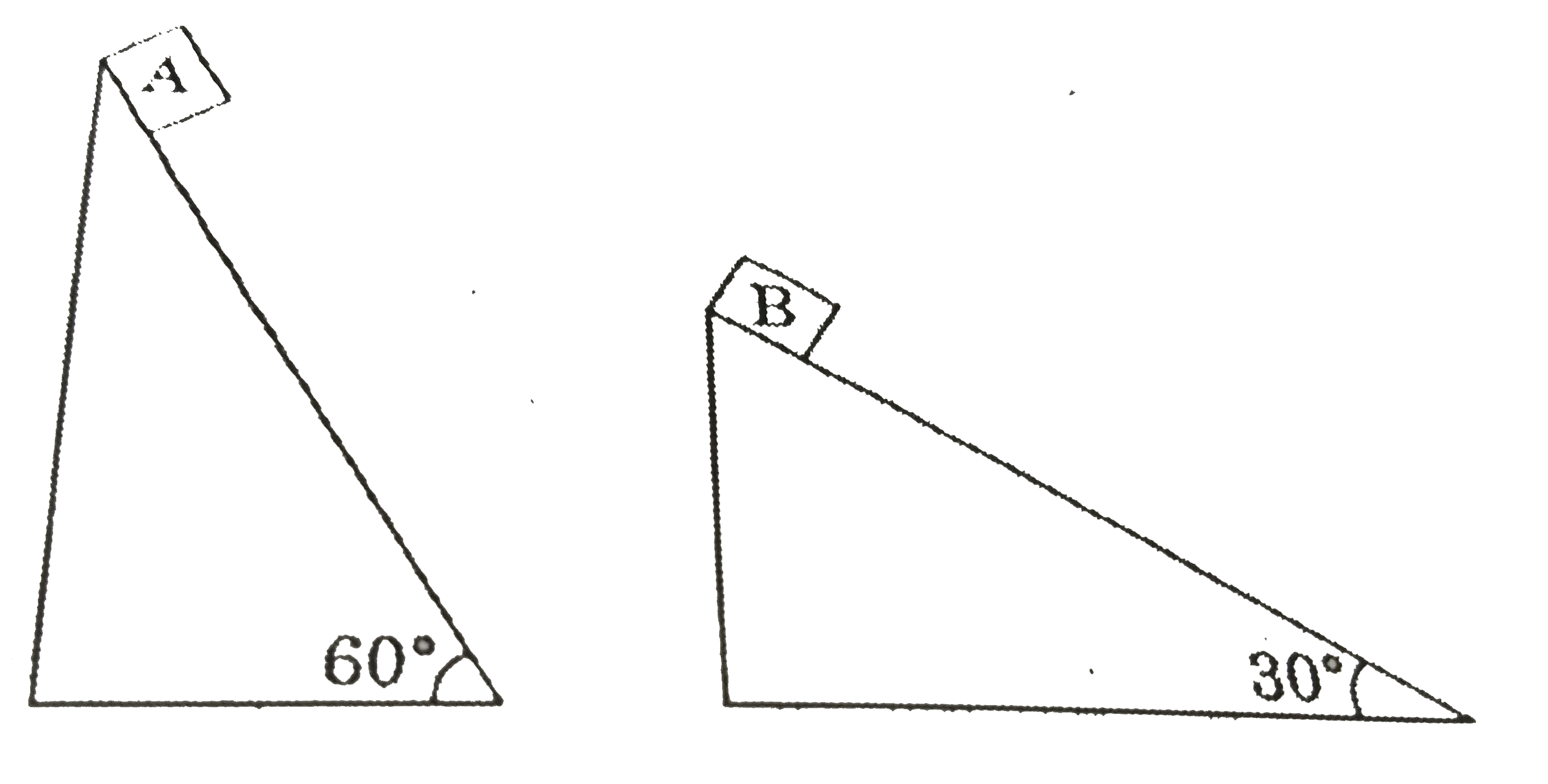
View SolutionTwo fixed frictionless inclined planes making an angle 30∘ and 60∘ with the vertical are shown in figure. Two blocks A and B are planes. What is the relative vertical acceleration of A with respect to B?
View Solution
Knowledge Check
Two stones are thrown from the same point with velocity of 5 ms−1 one vertically upwards and the other vertically downwards. When the first stone is at the highest point the relative velocity of the second stone with respect to the first stone is,
A5ms−1B0ms−1C10ms−1D−5ms−1
A particel slides from rest from the topmost point of a vertical circle of radirs r along a smooth chord making an angle θ with the vertical. The time of descent is .
View SolutionTwo particles start oscillating together in shm along the same straight line. Their periods are 2 s and 4 s. What is their phase difference afterls from the start?
View SolutionA particle slides down on a smooth incline of inclination 30∘, fixed in an elevator going up with an acceleration 2m/s2. The box of incline has width 4m. The time taken by the particle to reach the bottom will be

View SolutionTwo particles move with constant velocities towards point O along straight lines in a plane as shown. The shortest distance A and B is

View SolutionTwo particles are projected simultaneously with same speed V0 in same vertical plane at angle 30∘and60∘ With the horizontal .The time at which their velocities becomes parallel is
View SolutionTwo particles A and B starts from rest and move for equal time on a straight line. The particle A has an acceleration a for the first half of the total time and 2a for the second half. The particle B has an acceleration 2a for the first half and a for the second half. Which particle has covered larger distance?
View SolutionStarting from rest , a body slides down at 45∘ inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of friction between the body and the inclined plane is
View Solution
