A4m long ladder weighing 25kg rests with its upper and against a smooth wall and lower and on rought ground.What should be the minimum coefficient of friction between the ground and ladder for it to be inclined at 60∘ with the horizontal without slipping? (Takeg=10m/s2)
To solve the problem of determining the minimum coefficient of friction required for a ladder to remain stable against slipping, we can follow these steps:
Step 1: Identify the forces acting on the ladder
1. Weight (W): The weight of the ladder acts downwards at its center of mass, which is at the midpoint of the ladder. The weight can be calculated as:
W=mg=25kg×10m/s2=250N
2. Normal Force from the Ground (N2): This acts upwards at the base of the ladder.
3. Frictional Force (F): This acts horizontally at the base of the ladder, opposing the tendency to slip.
4. Normal Force from the Wall (N1): This acts horizontally at the top of the ladder, pushing it away from the wall.
Step 2: Set up the equilibrium conditions
For the ladder to be in equilibrium:
- The sum of vertical forces must equal zero.
- The sum of horizontal forces must equal zero.
- The sum of torques about any point must equal zero.
Step 3: Apply the vertical force equilibrium
From the vertical forces:
N2=W=250N
Step 4: Apply the horizontal force equilibrium
From the horizontal forces:
N1=F
Step 5: Apply the torque equilibrium
Choosing the base of the ladder (point A) to calculate torques:
- The torque due to N1 (acting at the top of the ladder) is:
τN1=N1⋅L⋅sin(60∘)
- The torque due to the weight W (acting at the midpoint of the ladder) is:
τW=W⋅(L2)⋅cos(60∘)
Setting the torques equal for equilibrium:
N1⋅L⋅sin(60∘)=W⋅(L2)⋅cos(60∘)
Step 6: Substitute known values
Substituting W=250N and L=4m:
N1⋅4⋅√32=250⋅2⋅12
This simplifies to:
N1⋅4⋅√32=250
N1⋅2√3=250
N1=2502√3=125√3N
Step 7: Relate friction and normal forces
The frictional force F can be expressed in terms of the coefficient of friction μ and the normal force from the ground N2:
F=μN2
Substituting N2=250N:
F=μ⋅250
Step 8: Set F=N1
From the horizontal equilibrium:
μ⋅250=125√3
Step 9: Solve for μ
μ=125250√3=12√3
Final Answer
The minimum coefficient of friction required is:
μ=12√3≈0.2887
1. Weight (W): The weight of the ladder acts downwards at its center of mass, which is at the midpoint of the ladder. The weight can be calculated as:
W=mg=25kg×10m/s2=250N
2. Normal Force from the Ground (N2): This acts upwards at the base of the ladder.
3. Frictional Force (F): This acts horizontally at the base of the ladder, opposing the tendency to slip.
4. Normal Force from the Wall (N1): This acts horizontally at the top of the ladder, pushing it away from the wall.
For the ladder to be in equilibrium:
- The sum of vertical forces must equal zero.
- The sum of horizontal forces must equal zero.
- The sum of torques about any point must equal zero.
From the vertical forces:
N2=W=250N
From the horizontal forces:
N1=F
Choosing the base of the ladder (point A) to calculate torques:
- The torque due to N1 (acting at the top of the ladder) is:
τN1=N1⋅L⋅sin(60∘)
- The torque due to the weight W (acting at the midpoint of the ladder) is:
τW=W⋅(L2)⋅cos(60∘)
N1⋅L⋅sin(60∘)=W⋅(L2)⋅cos(60∘)
Substituting W=250N and L=4m:
N1⋅4⋅√32=250⋅2⋅12
This simplifies to:
N1⋅4⋅√32=250
N1⋅2√3=250
N1=2502√3=125√3N
The frictional force F can be expressed in terms of the coefficient of friction μ and the normal force from the ground N2:
F=μN2
Substituting N2=250N:
F=μ⋅250
From the horizontal equilibrium:
μ⋅250=125√3
μ=125250√3=12√3
The minimum coefficient of friction required is:
μ=12√3≈0.2887
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Objective Question
Explore 32 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Comprehension
Explore 9 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Assertion And Reason
Explore 28 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEY ENGLISHChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
A car goes on a circular horizontal road of radius 100 m. What should be the minimum coefficient of friction between the tyres and the road so that it completes the circle with velocity 10 m/s without slipping ? (Take g=10m/s2)
View SolutionThe length of a uniform ladder of mass m is 1. It leans against a smooth wall making an angle θ with the horizontal. What should be the force of friction between the floor and ladder so that the ladder does not slip ?
View Solution
Knowledge Check
A 4m long ladder weighing 25kg rests with its upper end against a smooth wall and lower end on rough ground.What should be the minimum coefficient of friction between the ground and the ladder for it to be inclined at 60∘ with the horizontal without slipping? (Takeg=10m/s2)
Aa. 0.19Bb. 0.29Cc. 0.39Dd. 0.49
A ladder of mass 10kg is held at reat against a smooth wall on a rough ground as shown in figure. The normal reaction between the wall and the ladder is

View SolutionA ladder of length l and mass m is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is μ. The angle θ at which the ladder will stay in equilibrium is
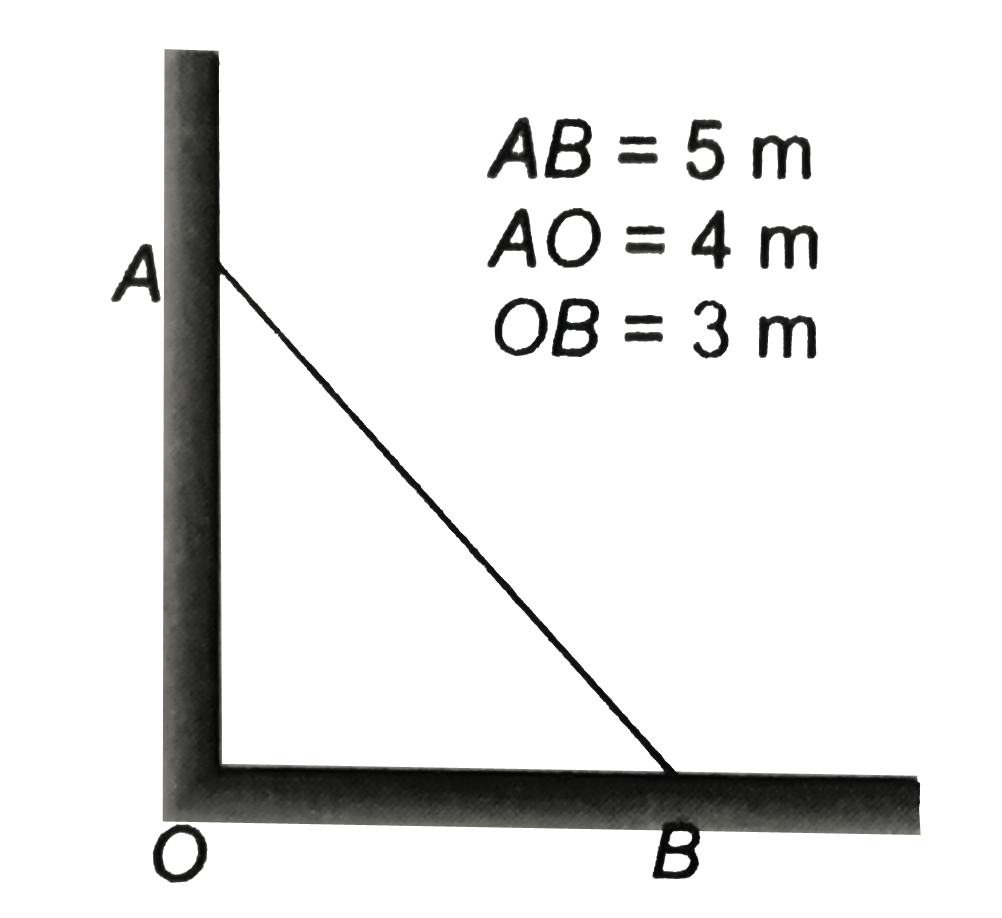
View SolutionA ladder of length 5m is placed against a smooth wall as shown in figure. The coefficient or friction is μ between ladder and ground. What is the minimum value of μ , If the ladder is not to slip?
View SolutionA ladder is kept at rest with is upper end against a wall and the lower end on the ground. The ladder is more like to slip when a mass stands on it at the top than at the bottom. Why ?
View SolutionA uniform ladder which is 5m long has a mass of 25kg , leans with its upper end against a smooth vertical wall and its lower end on rough ground. The bottom of the ladder is 3m from the wall. Calculate the frictional force between the ladder and the ground . (g=10ms−2)
View SolutionA ladder of length 5m is placed against a smooth wall as shown in figure. The coefficient or friction is μ between ladder and ground. What is the minimum value of μ , If the ladder is not to slip?

View SolutionA ladder of length 5m is placed against a smooth wall as shown in figure. The coefficient or friction is μ between ladder and ground. What is the minimum value of μ , If the ladder is not to slip?

View Solution