A plumb bob of mass 1kg is hung from the ceiling of a train compartment.The train moves on an inclined plane with constant velocity. If the angle of inclined is 30∘.Find the angle made by the string with the normal to the ceiling .Also ,Find the tension in the string (g=10m/s2)
To solve the problem, we need to determine two things: the angle made by the string with the normal to the ceiling and the tension in the string. Let's break this down step by step.
Step 1: Understanding the Situation
We have a plumb bob of mass m=1kg hanging from the ceiling of a train compartment. The train moves on an inclined plane with an angle of inclination θ=30∘.
Step 2: Analyzing Forces
Since the train is moving with constant velocity, we can assume that there are no net forces acting on the bob in the direction of the incline. The forces acting on the bob are:
1. The gravitational force mg acting downwards.
2. The tension T in the string acting along the string.
Step 3: Finding the Angle with the Normal
The normal to the ceiling is perpendicular to the ceiling. If we denote the angle that the string makes with the vertical (the direction of gravity) as ϕ, then we can relate ϕ to the angle of inclination θ.
Since the train is on an incline, the angle ϕ can be found using the geometry of the situation:
- The angle between the string and the normal to the ceiling will be 90∘−ϕ.
From the geometry, we can see that:
ϕ+30∘=90∘
Thus,
ϕ=90∘−30∘=60∘
Therefore, the angle made by the string with the normal to the ceiling is:
Angle with normal=30∘
Step 4: Finding the Tension in the String
To find the tension T in the string, we can analyze the forces acting on the bob. In the vertical direction, we have:
Tcos(30∘)=mg
Where g=10m/s2 and m=1kg.
Substituting the values:
Tcos(30∘)=1×10
T⋅√32=10
T=10√32=20√3≈11.55N
However, since we are asked for the tension in the string, we can round it to the nearest whole number:
T≈11.55N≈12N
Final Answers
1. The angle made by the string with the normal to the ceiling is 30∘.
2. The tension in the string is approximately 12N.
We have a plumb bob of mass m=1kg hanging from the ceiling of a train compartment. The train moves on an inclined plane with an angle of inclination θ=30∘.
Since the train is moving with constant velocity, we can assume that there are no net forces acting on the bob in the direction of the incline. The forces acting on the bob are:
1. The gravitational force mg acting downwards.
2. The tension T in the string acting along the string.
The normal to the ceiling is perpendicular to the ceiling. If we denote the angle that the string makes with the vertical (the direction of gravity) as ϕ, then we can relate ϕ to the angle of inclination θ.
- The angle between the string and the normal to the ceiling will be 90∘−ϕ.
ϕ+30∘=90∘
Thus,
ϕ=90∘−30∘=60∘
Angle with normal=30∘
To find the tension T in the string, we can analyze the forces acting on the bob. In the vertical direction, we have:
Tcos(30∘)=mg
Where g=10m/s2 and m=1kg.
Tcos(30∘)=1×10
T⋅√32=10
T=10√32=20√3≈11.55N
T≈11.55N≈12N
1. The angle made by the string with the normal to the ceiling is 30∘.
2. The tension in the string is approximately 12N.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Objective Question
32 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason
28 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A plumb bob is hung from the ceiling of a train compartment. If the train moves with an acceleration a along a straight horizontal track, the string supporting the bob makes an angle tan1(ag) with the normal to the ceiling. Suppose the train moves on an inclined straight track with uniform velocity, if the angle of incline is tan−1(ag), the string again makes the same angle with the normal to the ceiling. Can a person sitting inside the compartment tell by looking at the plumb line whether the train is accelerated on a horizontal straight track or it is going on an incline? If yes, how? If no, suggest a method to do so.
View SolutionA pendulum is hanging from the ceiling of a car having an acceleration a0 with respect to the road. Find the angle made by the string with vertical at equilibrium. Also find the tension in the sting in this position

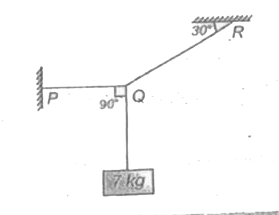
View SolutionFind the tension in the horizontal string PQ and the string QR in the given figure [ Take g =10m/s2]

View SolutionA bob of mass m is suspended from the ceiling of a train moving with an acceleration a as shown in figure. Find the angle θ in equilibrium position.
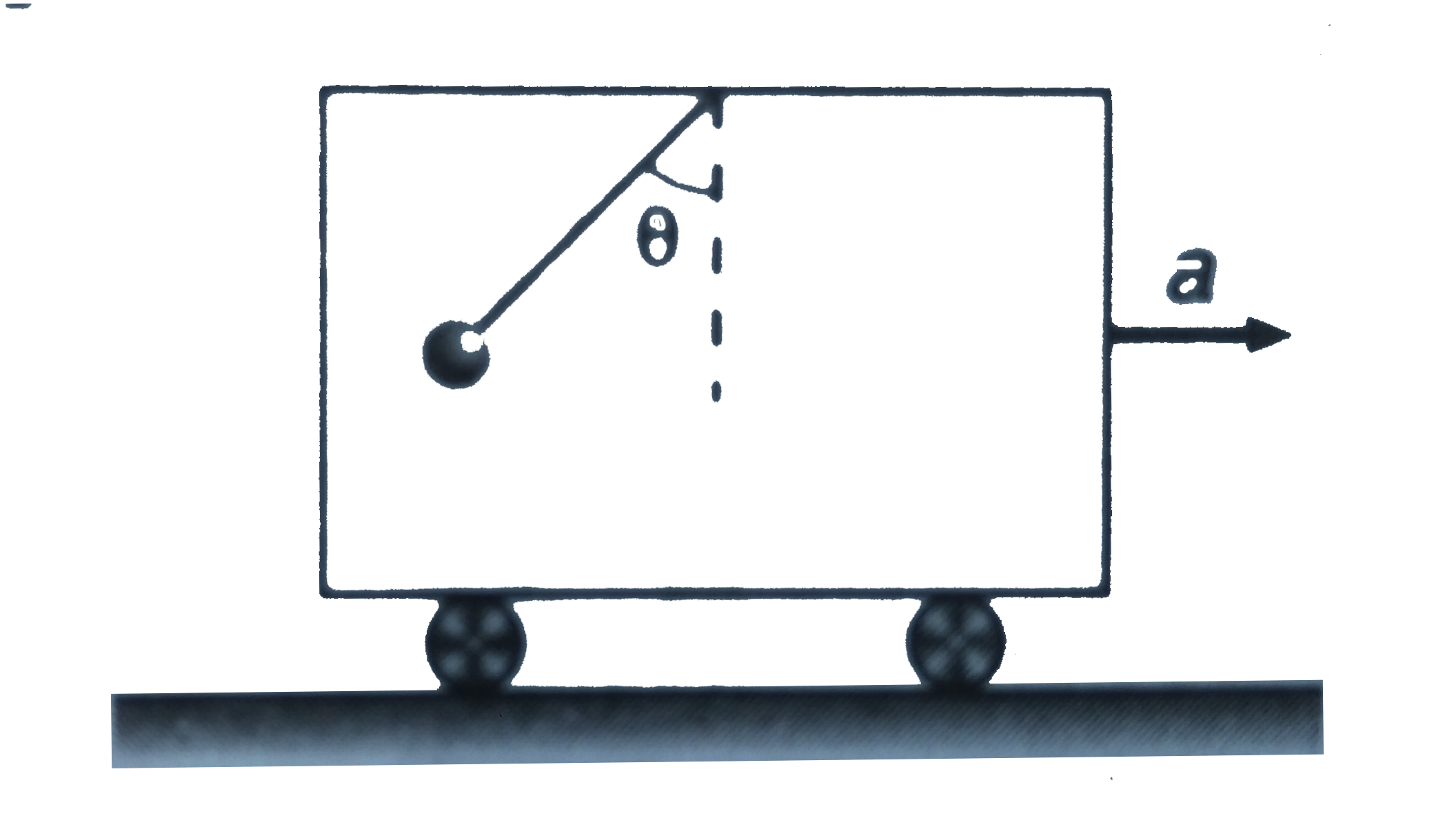
View SolutionFind the tension in the horizontal string PQ and the string QR in the given figure. [Take g=10m/s2]
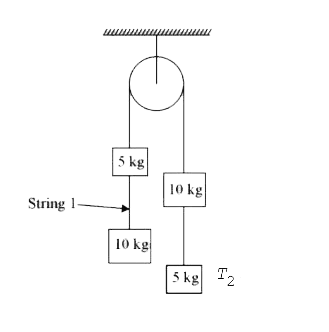
View SolutionFind the value of tension in string 1 if the system equilibrium ? (g=10 m/s2)
View SolutionA simple pendulum is suspended from the ceiling of trolley which is sliding down on a inclined plane of inclination θ Find the angle made by the string with normal to the trolley a) when trolley slides down with uniform velocity b) when the plane is smooth.
View SolutionConsider the situation shown in figure .Both the pulleys and the string and light and all the surfaces are smooth.
(a) Find the acceleration of 1kg block.
(b) Find the tension in the string. (g=10m/s2).

View SolutionA pendulum is hanging from the ceiling of a car having an acceleration a0 with respect to the road. Find the angle made by the string with the vertical.
View SolutionA simple pendulum having bob of mass m is suspended from the ceiling of a car used in a stunt film shooting. The car moves up along an inclined cliff at a speed v and makes a jump to leave the cliff and lands at some the top of the cliff. The tension in the string when the car is in air is
View Solution
