If a ladder weighting 250N in placed a smooth vertical wall having coefficient of friction between it and floor 0.3, then what is the maximum force of friction available at the point of contact between the ladder and the floor? a) 75 N b) 50 N c) 35 N d) 25 N
75N
50N
35N
25N
The correct Answer is:A
To solve the problem, we need to determine the maximum force of friction available at the point of contact between the ladder and the floor. Here are the steps to arrive at the solution:
1. Identify the Given Data:
- Weight of the ladder (W) = 250 N
- Coefficient of friction (μ) = 0.3
2. Understand the Forces Acting on the Ladder:
- The ladder has a weight acting downwards, which is balanced by the normal reaction force (R) from the floor acting upwards.
- Since the wall is smooth, it does not exert any horizontal friction force on the ladder.
3. Establish the Relationship Between Normal Force and Friction:
- The maximum force of friction (F) can be calculated using the formula:
F=μ⋅R
- Here, R is the normal reaction force, which is equal to the weight of the ladder (W) since there are no vertical accelerations.
4. Calculate the Normal Reaction Force (R):
- Since the ladder is in equilibrium:
R=W=250N
5. Substitute Values into the Friction Formula:
- Now, substitute the values into the friction formula:
F=μ⋅R=0.3⋅250N
6. Perform the Calculation:
- Calculate the maximum force of friction:
F=0.3⋅250=75N
7. Conclusion:
- The maximum force of friction available at the point of contact between the ladder and the floor is 75 N.
Final Answer:
- The correct option is a) 75 N.
- Weight of the ladder (W) = 250 N
- Coefficient of friction (μ) = 0.3
- The ladder has a weight acting downwards, which is balanced by the normal reaction force (R) from the floor acting upwards.
- Since the wall is smooth, it does not exert any horizontal friction force on the ladder.
- The maximum force of friction (F) can be calculated using the formula:
F=μ⋅R
- Here, R is the normal reaction force, which is equal to the weight of the ladder (W) since there are no vertical accelerations.
- Since the ladder is in equilibrium:
R=W=250N
- Now, substitute the values into the friction formula:
F=μ⋅R=0.3⋅250N
- Calculate the maximum force of friction:
F=0.3⋅250=75N
- The maximum force of friction available at the point of contact between the ladder and the floor is 75 N.
- The correct option is a) 75 N.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Objective Question
32 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason
28 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A uniform ladder of length 3.25 m and weight 250 N is placed against a smooth vertical wall with its lower end 1.25 m from the wall. If coefficient of friction between the ladder and the floor is 0.3, then, find the frictional force acting on the ladder at the point of contact between ladder and floor.
View SolutionA ladder of length 5m is placed against a smooth wall as shown in figure. The coefficient or friction is μ between ladder and ground. What is the minimum value of μ , If the ladder is not to slip?
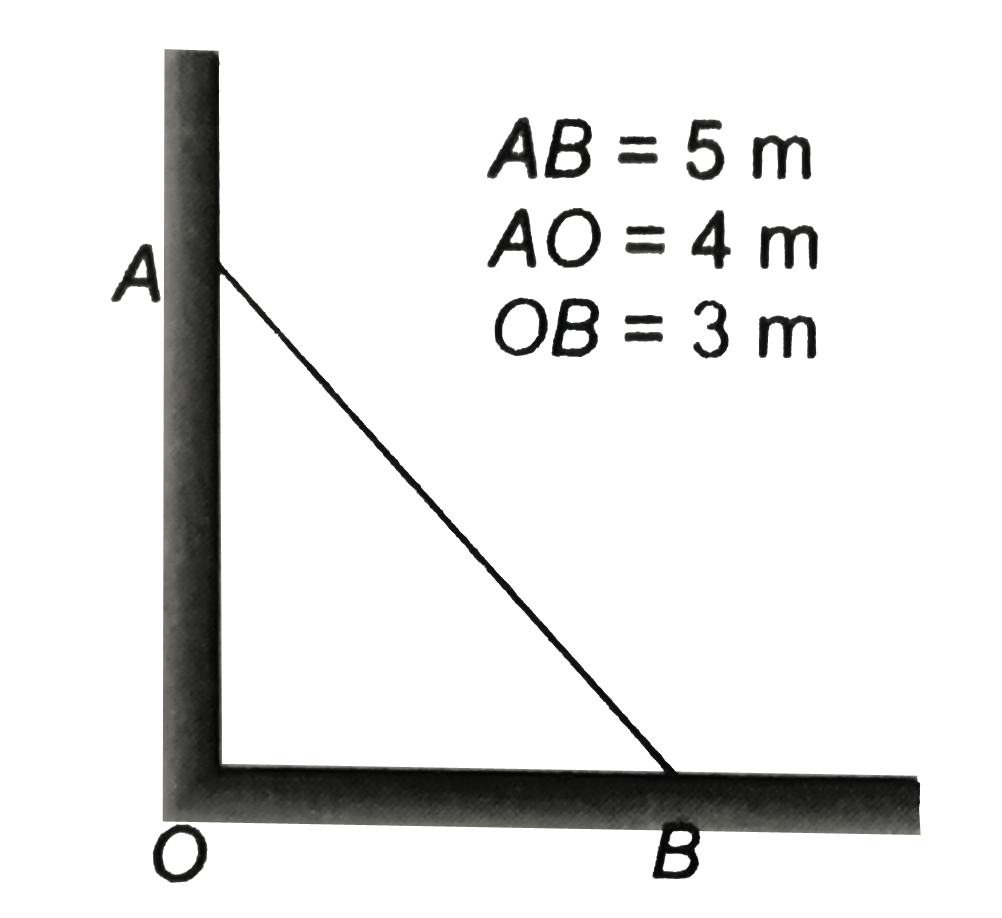
View SolutionA ladder of length 5m is placed against a smooth wall as shown in figure. The coefficient or friction is μ between ladder and ground. What is the minimum value of μ , If the ladder is not to slip?

View SolutionA block of weight 5 N is pushed against a vertical wall by a force 12 N . The coefficient of friction between the wall and block is 0.6 . Find the magnitude of the force exerted by the wall on the block :
View SolutionA ladder of length l and mass m is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is μ. The angle θ at which the ladder will stay in equilibrium is
View SolutionA crate of mass 20 kg is sliding across a wooden floor. The coefficient of kinetic friction between the crate and the floor is 0.3.
Determine the magnitude of the friction force acting on the crate.
View SolutionA crate of mass 20 kg is sliding across a wooden floor. The coefficient of kinetic friction between the crate and the floor is 0.3.
If the crate is being pulled by a force of 90 N (parallel to the floor), find the acceleration of the crate.
View SolutionBlock A of mass 2kg is placed over a block B of mass 8kg . The combination is placed on a rough horizontal surface. If g=10ms−2 , coefficient of friction between B and floor =0.5 , coefficient of friction between B and floor =0.5 , coefficient of friction between A and B=0.4 and a horizontal force of 10N is applied on 8kg block, then the force of friction between A and B is.

View SolutionBlock A of mass 2kg is placed over a block B of mass 8kg . The combination is placed on a rough horizontal surface. If g=10ms−2 , coefficient of friction between B and floor =0.5 , coefficient of friction between B and floor =0.5 , coefficient of friction between A and B=0.4 and a horizontal force of 10N is applied on 8kg block, then the force of friction between A and B is.

View SolutionA block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
View Solution
