Two particles each of mass m are connected by a light inextensible string and a particle of mass M is attached to the midpoint of the string. The system is at rest on a smooth horizontal table with string just taut and in a straight line. The particle M is given a velocity v along the table perpendicular to the string. Prove that when the two particles are about to collide :
(i) The velocity of M is Mv(M+2m)
(ii) The speed of each of the other particles is (√2M(M+m)(M+2m))v.
To solve the problem step by step, we will analyze the system of particles and apply the principles of conservation of momentum and energy.
Step 1: Understand the System
We have two particles, each of mass m, connected by a light inextensible string. A particle of mass M is attached to the midpoint of the string. Initially, the system is at rest, and then the particle M is given a velocity v perpendicular to the string.
Step 2: Apply Conservation of Linear Momentum
When particle M moves with velocity v, it will exert forces on the two particles of mass m. Since the system is isolated, the total momentum before and after must be conserved.
The initial momentum of the system is:
Pinitial=0
The final momentum when the two particles are about to collide can be expressed as:
Pfinal=Mv+mv1+mv2
where v1 and v2 are the velocities of the two particles of mass m.
According to the conservation of momentum:
0=Mv+mv1+mv2
Since both particles are identical and will have the same speed when they collide, we can set v1=v2=v′:
0=Mv+2mv′
Rearranging gives:
2mv′=−Mv⟹v′=−Mv2m
Step 3: Find the Velocity of Particle M
To find the velocity of particle M when the two particles are about to collide, we can use the center of mass (COM) concept. The velocity of the center of mass VCOM is given by:
VCOM=M⋅v+2m⋅0M+2m=MvM+2m
Step 4: Calculate the Speed of Each Particle
Now, we need to find the speed of each of the particles of mass m. We can use the conservation of energy principle. The kinetic energy of the system must also be conserved.
The initial kinetic energy when particle M is given velocity v is:
KEinitial=12Mv2
The final kinetic energy when the two particles are about to collide is:
KEfinal=12MV2M+2⋅12mv′2
Substituting v′=−Mv2m:
KEfinal=12MV2M+m(−Mv2m)2
=12MV2M+M2v28m
Setting KEinitial=KEfinal:
12Mv2=12MV2M+M2v28m
Solving for VM:
Mv2=MV2M+M2v24m
MV2M=Mv2−M2v24m
V2M=v2(1−M4m)
VM=v√4m−M4m=MvM+2m
Final Answers
1. The velocity of M is:
VM=MvM+2m
2. The speed of each of the other particles is:
v′=√2MM+mM+2mv
We have two particles, each of mass m, connected by a light inextensible string. A particle of mass M is attached to the midpoint of the string. Initially, the system is at rest, and then the particle M is given a velocity v perpendicular to the string.
When particle M moves with velocity v, it will exert forces on the two particles of mass m. Since the system is isolated, the total momentum before and after must be conserved.
Pinitial=0
The final momentum when the two particles are about to collide can be expressed as:
Pfinal=Mv+mv1+mv2
where v1 and v2 are the velocities of the two particles of mass m.
0=Mv+mv1+mv2
Since both particles are identical and will have the same speed when they collide, we can set v1=v2=v′:
0=Mv+2mv′
Rearranging gives:
2mv′=−Mv⟹v′=−Mv2m
To find the velocity of particle M when the two particles are about to collide, we can use the center of mass (COM) concept. The velocity of the center of mass VCOM is given by:
VCOM=M⋅v+2m⋅0M+2m=MvM+2m
Now, we need to find the speed of each of the particles of mass m. We can use the conservation of energy principle. The kinetic energy of the system must also be conserved.
KEinitial=12Mv2
The final kinetic energy when the two particles are about to collide is:
KEfinal=12MV2M+2⋅12mv′2
Substituting v′=−Mv2m:
KEfinal=12MV2M+m(−Mv2m)2
=12MV2M+M2v28m
12Mv2=12MV2M+M2v28m
Solving for VM:
Mv2=MV2M+M2v24m
MV2M=Mv2−M2v24m
V2M=v2(1−M4m)
VM=v√4m−M4m=MvM+2m
1. The velocity of M is:
VM=MvM+2m
2. The speed of each of the other particles is:
v′=√2MM+mM+2mv
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V A
20 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A
32 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
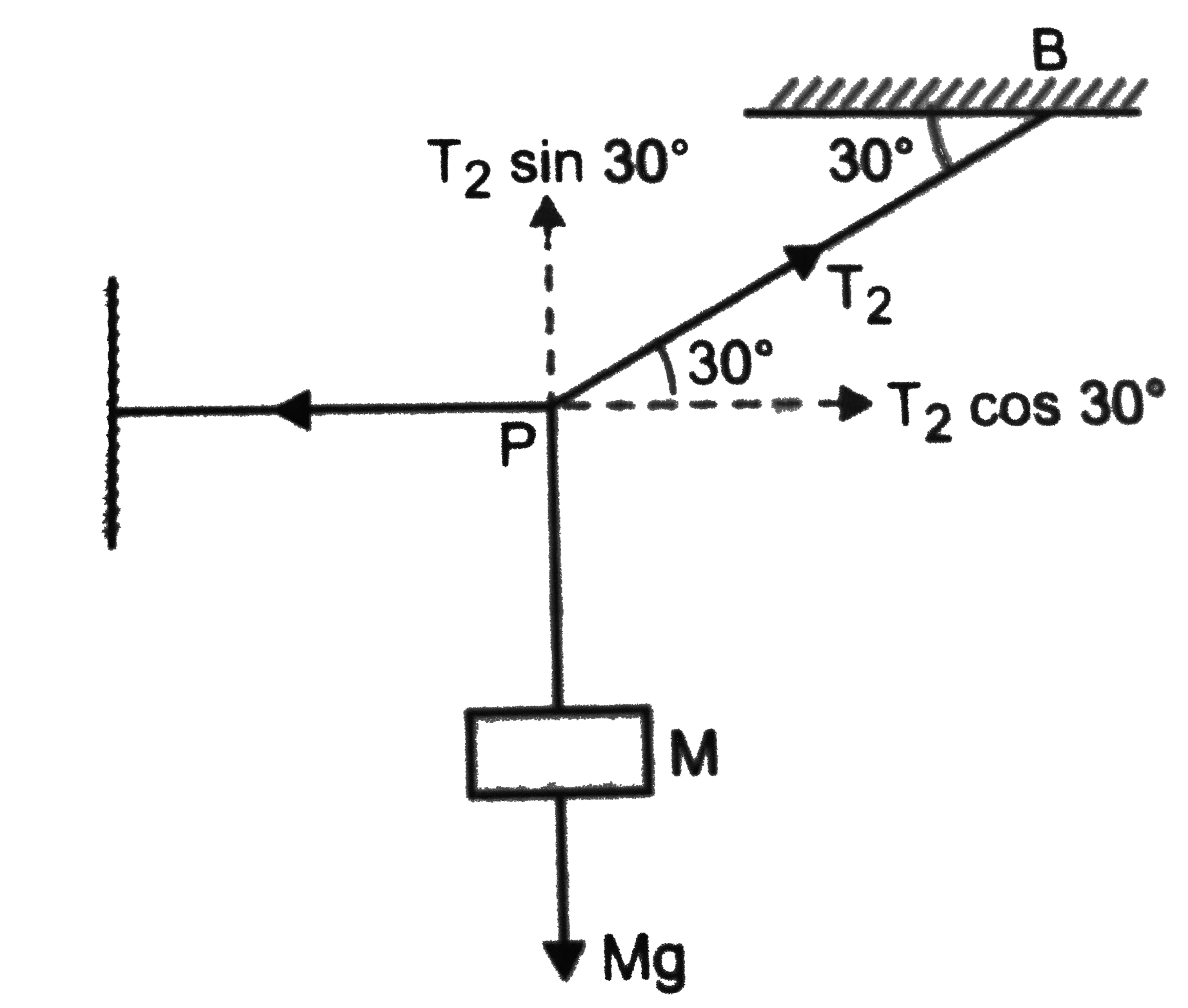
A mass M is hung with a light inextensible string as shown in Find the tension in the horizontal part of the string .
View SolutionTwo particles of a mass 2m and m are tied with an inextensible string the particle of mass m is given a speed V as shown in the figure. Find the speed with which the particle of mass 2m starts moving.
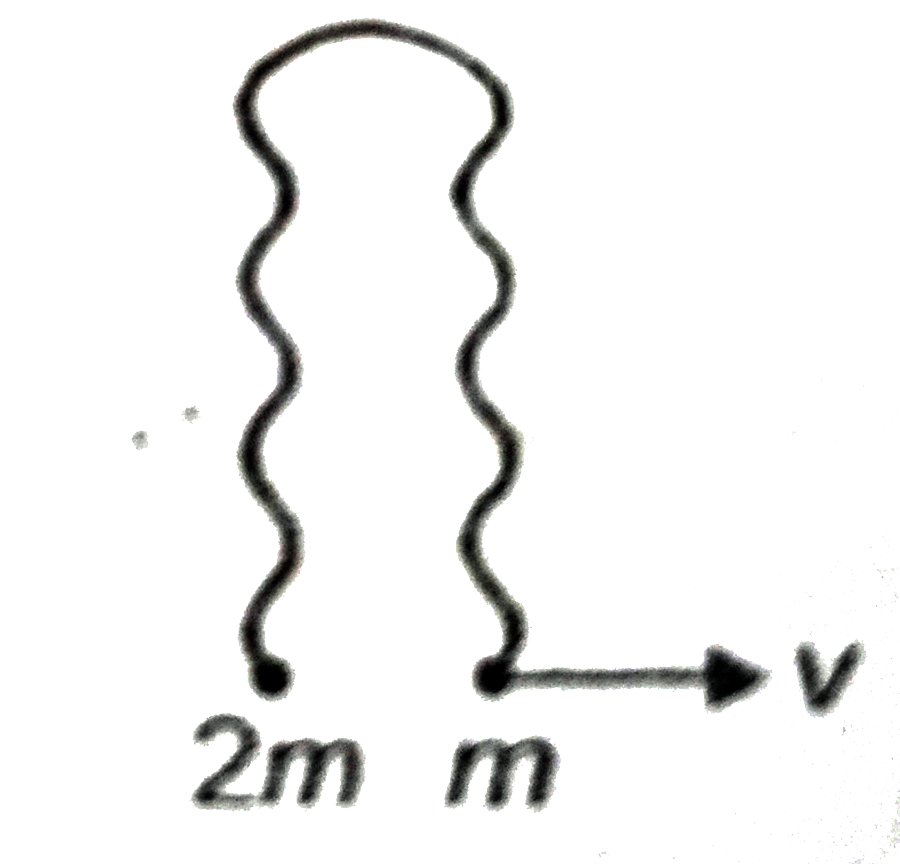
View SolutionTwo particles of a mass 2m and m are tied with an inextensible string the particle of mass m is given a speed V as shown in the figure. Find the speed with which the particle of mass 2m starts moving.

View SolutionTwo blocks of masses m and M are connected by an inextensible light string . When a constant horizontal force acts on the block of mass M. The tension in the string is

View SolutionTwo particles having mass ratio n:1 are interconnected by a light inextensible string that passes over a smooth pulley . If the system is released , then the acceleration of the centre of mass of the system is
View SolutionTwo particles of masses m1andm2 are connected to a string and the system is rotated in a horizontal plane with 'P' as center. The ratio of tension in the two parts of string is

View SolutionA particle of maas m is attched to a light string of length l, the other end of which is fixed. Initially the string is kept horizontal and the particle is given an upwrd velocity v. The particle is just able to complete a circle
View SolutionA particle of mass 2m is connected by an inextensible string of length 1.2m to a ring of mass m which is free to slide on a horizontal smooth rod. Initially the ring and the particle are at the same level with the string taut. Both are then released simultaneously. The distance in meter moved by the ring when the string becomes veritcal is :-
View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl

The maximum angle made by the string with downward vertical is
View Solution
