Two blocks of masses m1 and m2 are connected by a massless pulley A, slides along th esmooth sides of a rectangular wedge of mass m, which rests on a smooth horizontal plane. Find the distance covered by the wedge on the horizontal plane till the mass m1 is lowered by the vertical distance h.
The correct Answer is:(m2+m1cotα)hm+m1+m2
To solve the problem, we will analyze the motion of the two blocks and the wedge. The key is to understand the relationship between the vertical movement of mass m1 and the horizontal movement of the wedge.
1. Understanding the System:
- We have two masses m1 and m2 connected by a pulley. The mass m1 is hanging vertically, while m2 is on the wedge which is on a smooth horizontal surface. The wedge has a mass m.
- The angle of the wedge with the horizontal is denoted as α.
2. Vertical Movement of m1:
- When mass m1 is lowered by a vertical distance h, it will cause the wedge to move horizontally.
3. Horizontal Movement of the Wedge:
- As m1 moves down by h, the length of the string on the side of the wedge also changes. The horizontal component of this movement can be expressed in terms of the angle α.
- The horizontal distance x moved by the wedge can be related to h by the geometry of the situation:
x=h⋅tan(α)
4. Using the Geometry of the Wedge:
- The distance x that the wedge moves horizontally can be derived from the fact that the vertical drop of m1 translates into a horizontal movement of the wedge.
- Since the wedge moves horizontally while m1 moves vertically, we can use the relationship:
Horizontal distance moved by wedge=h⋅tan(α)
5. Final Expression:
- Therefore, the distance d covered by the wedge on the horizontal plane until m1 is lowered by the vertical distance h is given by:
d=h⋅tan(α)
Final Answer:
The distance covered by the wedge on the horizontal plane till the mass m1 is lowered by the vertical distance h is d=h⋅tan(α).
- We have two masses m1 and m2 connected by a pulley. The mass m1 is hanging vertically, while m2 is on the wedge which is on a smooth horizontal surface. The wedge has a mass m.
- The angle of the wedge with the horizontal is denoted as α.
- When mass m1 is lowered by a vertical distance h, it will cause the wedge to move horizontally.
- As m1 moves down by h, the length of the string on the side of the wedge also changes. The horizontal component of this movement can be expressed in terms of the angle α.
- The horizontal distance x moved by the wedge can be related to h by the geometry of the situation:
x=h⋅tan(α)
- The distance x that the wedge moves horizontally can be derived from the fact that the vertical drop of m1 translates into a horizontal movement of the wedge.
- Since the wedge moves horizontally while m1 moves vertically, we can use the relationship:
Horizontal distance moved by wedge=h⋅tan(α)
- Therefore, the distance d covered by the wedge on the horizontal plane until m1 is lowered by the vertical distance h is given by:
d=h⋅tan(α)
The distance covered by the wedge on the horizontal plane till the mass m1 is lowered by the vertical distance h is d=h⋅tan(α).
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V A20videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B19videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A32videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
Similar Questions
A block of mass 'm' is kept on a smooth moving wedge. If the acceleration of the wedge is 'a'
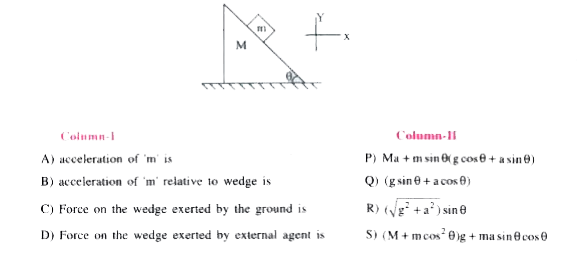 View Solution
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released
 View Solution
View SolutionA particle of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. Then the distance moved by the wedge as the particle reaches the foot of the wedge is :
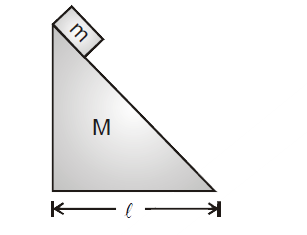 View Solution
View SolutionTwo blocks of masses m1 and m2, connected by a weightless spring of stiffness k rest on a smooth horizontal plane as shown in Fig. Block 2 is shifted a small distance x to the left and then released. Find the velocity of centre of mass of the system after block 1 breaks off the wall.
 View Solution
View SolutionA horizontal force F pushes wedge of mass M on a smooth horizontal surface. A block of mass m is stationary to the wedge, then:
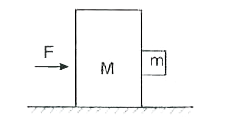 View Solution
View SolutionA block of mass m rests on a stationary wedge of mass M. The wedge can slide freely on a smooth horizontal surface as shown in figure. If the block starts from rest
 View Solution
View SolutionTwo smooth blocks of masses m and m' connected by a light inextensible strings are moving on a smooth wedge of mass M. If a force F acts on the wedge the blocks do not slide relative to the wedge. Find the (a) acceleration of the wedge and (b) value of F.
 View Solution
View SolutionTwo smooth blocks of masses m and m' connected by a light inextensible strings are moving on a smooth wedge of mass M. If a force F acts on the wedge the blocks do not slide relative to the wedge. Find the (a) acceleration of the wedge and (b) value of F.
 View Solution
View SolutionTwo smooth blocks of masses m and m' connected by a light inextensible strings are moving on a smooth wedge of mass M. If a force F acts on the wedge the blocks do not slide relative to the wedge. Find the (a) acceleration of the wedge and (b) value of F.
 View Solution
View SolutionA smooth wedge of mass M rests on a smooth horizontal surface. A block of mass m is projected from its lowermost point with velocity v0. What is the maximum height reached by the block?
 View Solution
View Solution
