A time dependent force F=6t acts on a particle of mass 1kg. If the particle starts from rest, the work done by the force during the first 1sec. will be
→E∞−B0csin(kx+ωt)ˆkV/m
→E=B0csin(kx−ωt)ˆkV/m
→E=B0csin(kx+ωt)ˆkV/m
→E=B0csin(kx+ωt)ˆkV/m
The correct Answer is:C
To solve the problem of finding the work done by the force F=6t on a particle of mass 1kg during the first second, we can follow these steps:
Step 1: Identify the force and mass
Given:
- Force F(t)=6t
- Mass m=1kg
Step 2: Calculate acceleration
Using Newton's second law, we know that:
F=m⋅a
Thus, the acceleration a can be expressed as:
a=Fm=6t1=6t
Step 3: Relate acceleration to velocity
Acceleration is the derivative of velocity with respect to time:
a=dvdt
So we can write:
dvdt=6t
Step 4: Integrate to find velocity
Integrate both sides with respect to time from t=0 to t=1:
∫v0dv=∫106tdt
The left side integrates to v, and the right side evaluates as follows:
∫106tdt=6⋅t22∣∣10=6⋅122−6⋅022=3
Thus, we find:
v=3m/s
Step 5: Calculate work done
The work done W is equal to the change in kinetic energy:
W=ΔKE=KEfinal−KEinitial
Since the particle starts from rest, the initial kinetic energy is zero:
KEinitial=0
The final kinetic energy is given by:
KEfinal=12mv2=12⋅1⋅(3)2=12⋅1⋅9=92J
Thus, the work done by the force during the first second is:
W=92J
Final Answer
The work done by the force during the first second is 92J.
---
Given:
- Force F(t)=6t
- Mass m=1kg
Using Newton's second law, we know that:
F=m⋅a
Thus, the acceleration a can be expressed as:
a=Fm=6t1=6t
Acceleration is the derivative of velocity with respect to time:
a=dvdt
So we can write:
dvdt=6t
Integrate both sides with respect to time from t=0 to t=1:
∫v0dv=∫106tdt
The left side integrates to v, and the right side evaluates as follows:
∫106tdt=6⋅t22∣∣10=6⋅122−6⋅022=3
Thus, we find:
v=3m/s
The work done W is equal to the change in kinetic energy:
W=ΔKE=KEfinal−KEinitial
Since the particle starts from rest, the initial kinetic energy is zero:
KEinitial=0
The final kinetic energy is given by:
KEfinal=12mv2=12⋅1⋅(3)2=12⋅1⋅9=92J
Thus, the work done by the force during the first second is:
W=92J
The work done by the force during the first second is 92J.
Topper's Solved these Questions
- JEE MAINSBook:JEE MAINS PREVIOUS YEAR ENGLISHChapter:JEE MAINSExercise:Chemistry
Explore 1 Video
- JEE MAINBook:JEE MAINS PREVIOUS YEAR ENGLISHChapter:JEE MAINExercise:All Questions
Explore 452 Videos
- JEE MAINS 2020Book:JEE MAINS PREVIOUS YEAR ENGLISHChapter:JEE MAINS 2020Exercise:PHYSICS
Explore 250 Videos
Similar Questions
Force acting on a particle varies with displacement as shown in figure. Find the total work done by the force.
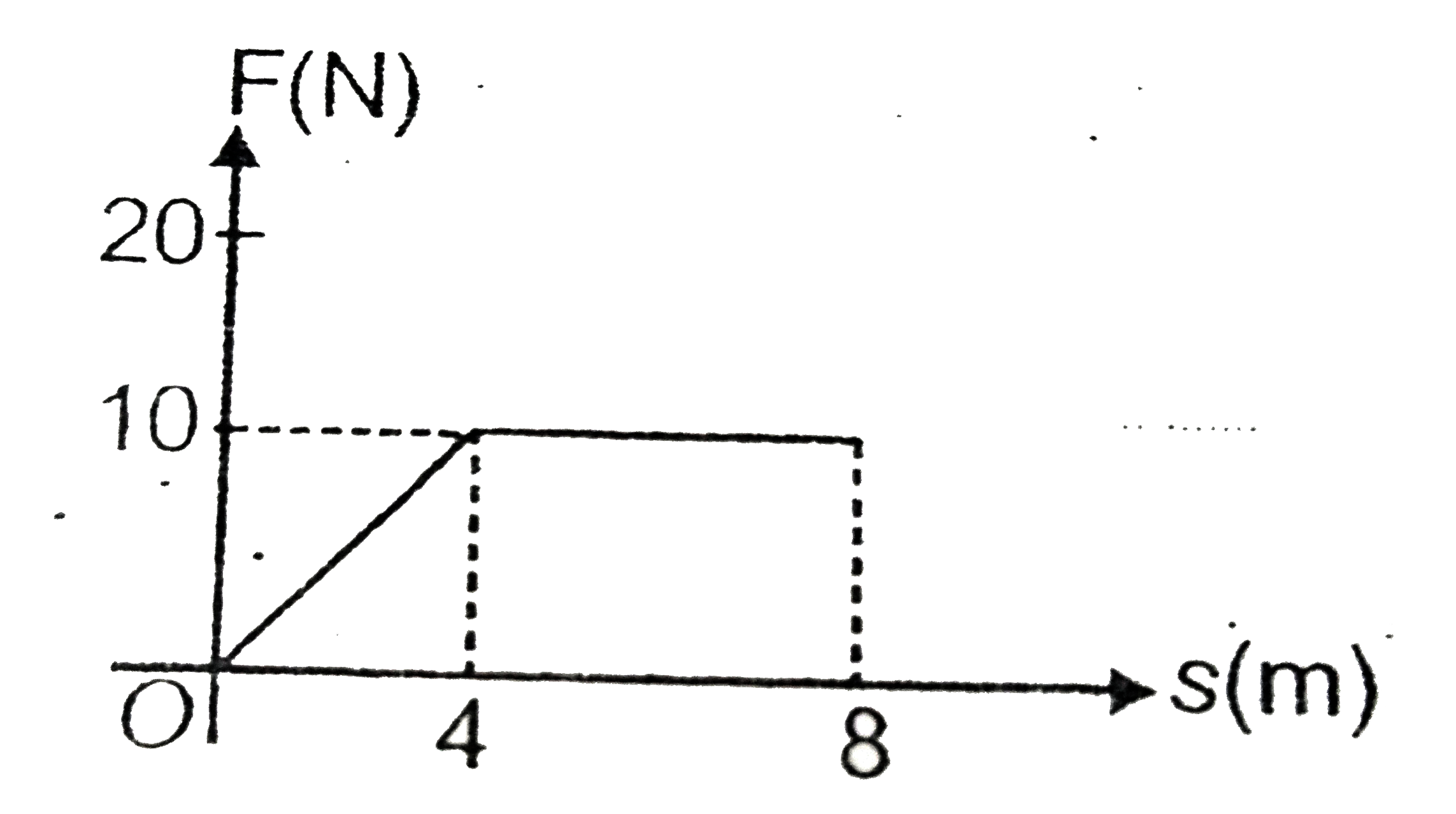
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View SolutionA force F=a+bx acts on a particle in x-direction, where a and b are constants. Find the work done by this force during the displacement from x1 to x2.
View SolutionA force given by the relation F=8t, acts on a body of mass 2kg, initialiy at rest. Find the work done by this force on the body during first 2 seconds of its motion.
View SolutionA tangential force of F = 1.5 N acts on a particle of mass m = 2 kg revolving in a circular path of radius r = 3 m. What is the work done by the torque for a complete revolution of the particle ?
View SolutionA force →F=(2xˆi+3ˆj+3z2ˆk) is acting on the particle of mass 2kg which is displaces from point A(2,3,0) to point B(3,2,1). the work done by the force on the particle will be
View SolutionA position dependent force F acting on a particle and its force-position curve is shown in the figure. The work done by force from x=1 m to x=4 m is
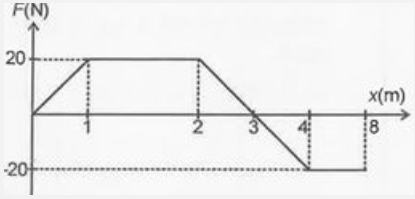
View SolutionA particle of mass 100g is thrown vertically upwards with a speed of 5m/s. The work done by the force of gravity during the time the particle goes up is
View SolutionA force f=10+2x acts on a particle moving in straight line on x axis the work done by this force during a displacement from x=0 and x=3m
View SolutionA force F1 acts on a particle so as to accelerate it from rest to a velocity v. The force F1 is then replaced by F2 which decelerates it to rest
View Solution