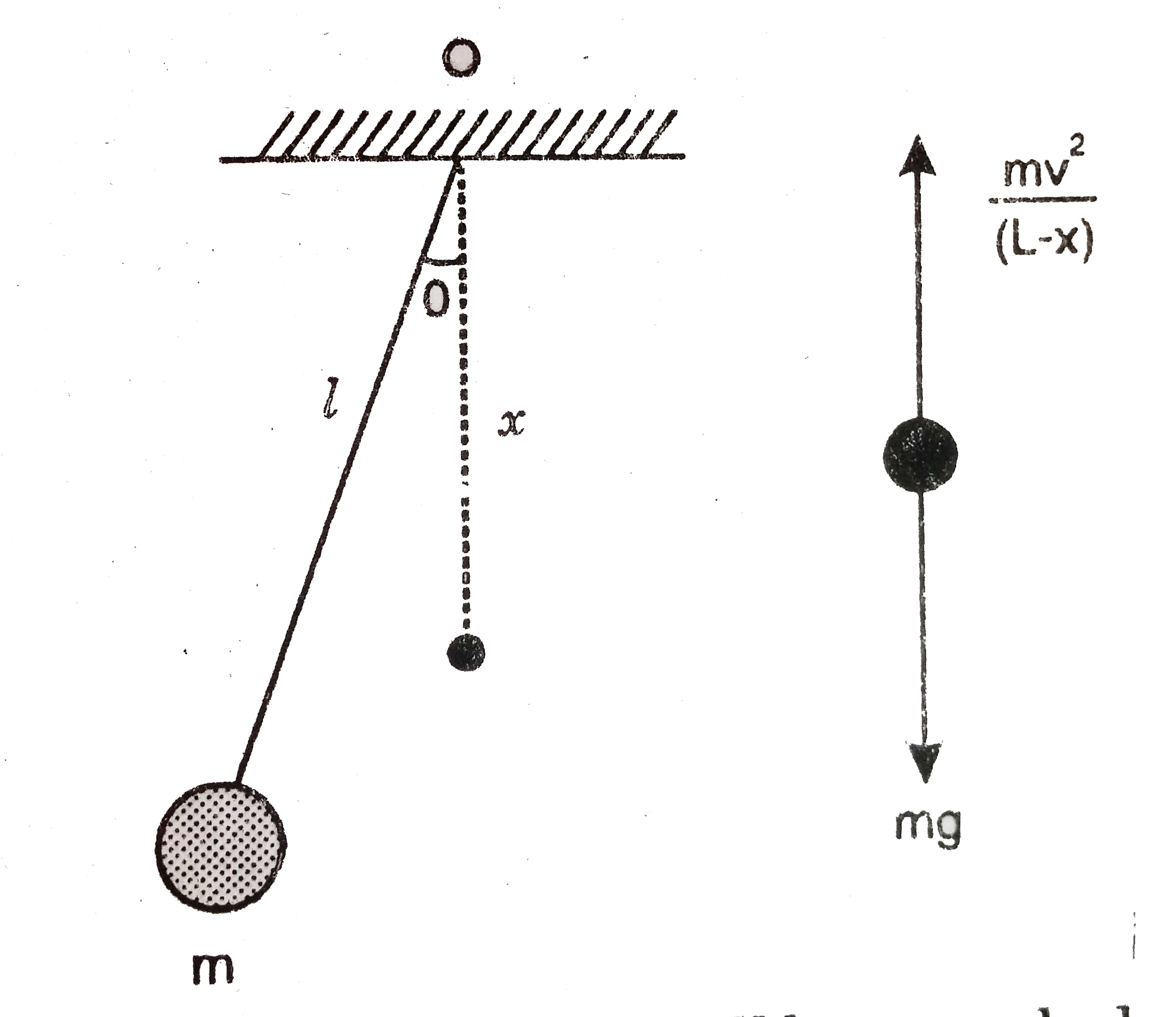
A simple pendulum of length L having a bob of mass m is deflected from its rest position by an angle $θ$ and released figure. The string hits a peg which is fixed at distance x below the point of suspension and the bob starts going in a circle centred at the peg. a. Assuming that initially the bob has a height less thasn the peg, show that the maximum height reached by the bob equals its initialheight. b. If the pendulum is released with $θ = 90^{0}$ and $m = \frac{L}{2}$ find the maximum height reached by the bob above its lowest positon before the string becomes slack. c. Find the minimum value of x/L for which the bob goes in a complete circle about the pet when the pendulum is released from $θ = 90^{0}$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C

a. When the bob has an initial height less than the peg and the released from rest ure let body travels from A to B since, total energy at A
$= T o t a l e \neq r g y a t B, < b r >$ :.(KE)_A+(PE)_A=(KE)_B+(PE)_B $< b r >$ rarr(PE)_=(PE)_A $< b r > ∵$ (KE)A=(KE)_B=0 $< b r > S o t h e max i μ m h e i g h t r e a c h e d b y t h e b o b i s e q u a l \to \in i t i a l h e i g h t . < b r > b . W h e n t h e p e n d u - - m i s r e \leq a s e d w i t h$ theta ==90^0 and x=l/2, ure the path of the particle is shown in ure.

At point C the string wil becomke slack and so the particle wil start making projectile motion.
Apply law of conservation.
$(\frac{1}{2}) m v_{c}^{2} - 0 = m g (\frac{L}{2}) (1 - cos α)$
[because distance between A and C ]
In the vertical direction is
$\frac{L}{2} = (1 - cos α)$
$\to V_{c}^{4} = g L (1 - cos α)$ ............i
Again, from the feebody diagram ure
$\frac{m v_{c}^{2}}{\frac{L}{2}} = m g cos α$ ......ii
$[b e c u s e T_{C} = 0]$
From equation i and equation ii
$g L (1 - cos α) = \frac{g L}{2} cos α$
$\to 1 - cos α = \frac{1}{2} cos α$
$\to \frac{3}{2} cos α = 1$
$\to cos α = (\frac{2}{3})$ ......iii
to find highest positon $C_{1}$ before the string becomes slack.
$B F = \frac{L}{2} + \frac{L}{2} cos θ$
$= \frac{L}{2} + \frac{L}{2} \times \frac{2}{3}$
$= L (\frac{1}{2} + \frac{1}{3})$
So, $B F = (\frac{5 L}{6})$
c. If the principle has to complete a vertical circle at the point C
$\frac{m v_{c}^{2}}{L - x} = m g$ .......i
Again applying energy principle between A and C
$(\frac{1}{2}) m v_{c}^{2} - 0 = m g (O C)$
$\to (\frac{1}{2}) m v_{c}^{2} = m g (L - 2 (l - x))$
$= m g (2 x - L)$
$\to v_{c}^{2} = 2 g (2 x - L)$ .......ii
From equation i and ii
$g (L - x) = 2 g (2 x - L)$
$\to L - x = 4 x - 2 L$
$\to 5 x = 3 L$
$∴ \frac{x}{L} = \frac{3}{5} = 0.6$
So, the rates $(\frac{x}{L})$ should be 0.6.

Updated on:21/07/2023

|

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

HC VERMA ENGLISH-WORK AND ENERGY-Exercises

Home
Ask Doubt
Profile