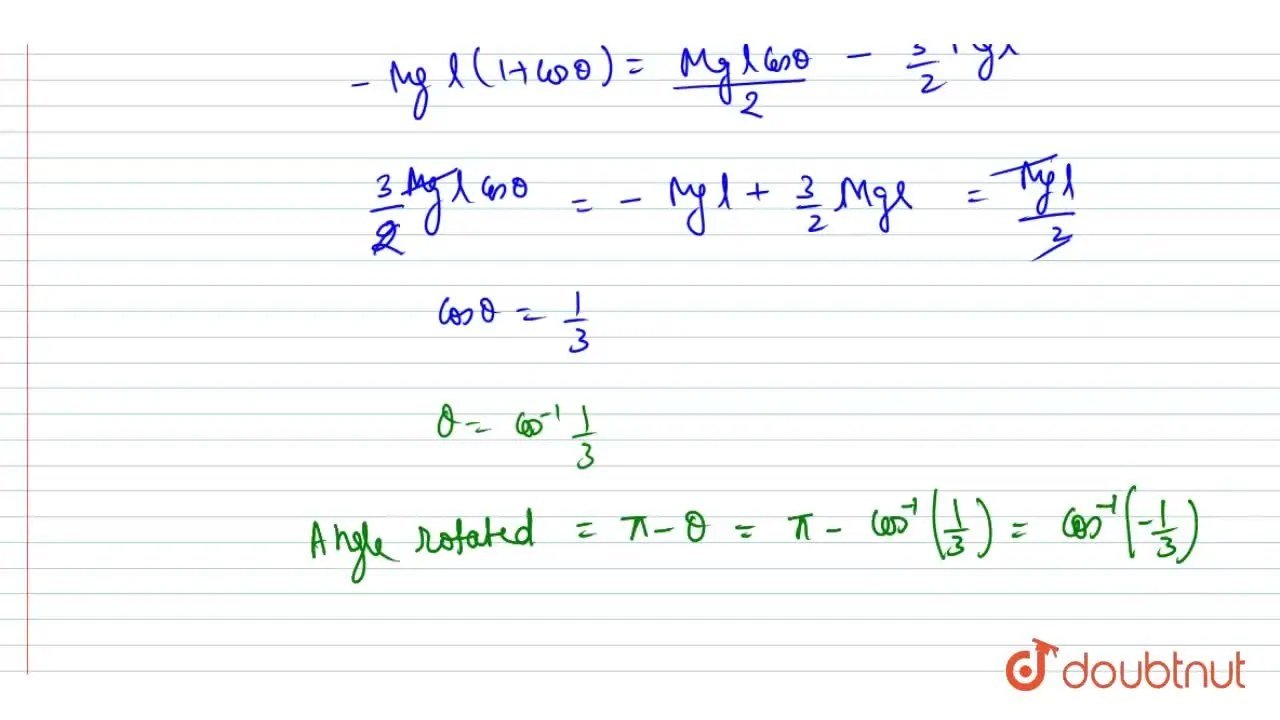The bob of a stationary pendulum is given a sharp hit to impart it a horizontal speed of √3gl. Find the angle rotated by the string before it becomes slack.
The correct Answer is:A, C
To solve the problem of finding the angle rotated by the string of a pendulum before it becomes slack after being given a horizontal speed of √3gl, we can follow these steps:
Step 1: Understand the Initial Conditions
The pendulum bob is initially stationary and is given a sharp hit to impart a horizontal speed of √3gl. At this point, we need to analyze the motion of the bob as it swings upward.
Hint: Identify the initial speed and the forces acting on the bob when it starts moving.
Step 2: Apply the Work-Energy Theorem
According to the work-energy theorem, the work done by gravity on the bob will equal the change in kinetic energy. The height the bob rises can be expressed in terms of the angle θ as:
h=l+lcosθ=l(1+cosθ)
The work done by gravity is:
W=−mg⋅h=−mg⋅l(1+cosθ)
Hint: Remember that the work done by gravity is negative because it acts downward while the bob moves upward.
Step 3: Write the Change in Kinetic Energy
The change in kinetic energy can be expressed as:
ΔKE=12mv′2−12mv2
Where:
- v′=0 at the highest point (when the string becomes slack)
- v=√3gl
Thus,
ΔKE=0−12m(3gl)=−32mgl
Hint: The kinetic energy at the highest point is zero since the bob momentarily stops before falling back down.
Step 4: Set Up the Equation
Equating the work done by gravity to the change in kinetic energy, we have:
−mgl(1+cosθ)=−32mgl
Cancelling mgl from both sides gives:
−(1+cosθ)=−32
Hint: Simplify the equation to isolate cosθ.
Step 5: Solve for cosθ
Rearranging the equation yields:
1+cosθ=32
Thus,
cosθ=32−1=12
Hint: Use the properties of cosine to find the angle.
Step 6: Find the Angle θ
The angle θ can be found using the inverse cosine function:
θ=cos−1(12)=π3
Hint: This angle is the angle from the vertical position.
Step 7: Calculate the Angle Rotated
The angle rotated by the string before it becomes slack is given by:
Angle rotated=π−θ=π−π3=2π3
Hint: Remember that the total angle rotated is measured from the vertical position.
Final Answer
The angle rotated by the string before it becomes slack is 2π3 radians.
---
The pendulum bob is initially stationary and is given a sharp hit to impart a horizontal speed of √3gl. At this point, we need to analyze the motion of the bob as it swings upward.
According to the work-energy theorem, the work done by gravity on the bob will equal the change in kinetic energy. The height the bob rises can be expressed in terms of the angle θ as:
The change in kinetic energy can be expressed as:
- v′=0 at the highest point (when the string becomes slack)
- v=√3gl
Equating the work done by gravity to the change in kinetic energy, we have:
Rearranging the equation yields:
The angle θ can be found using the inverse cosine function:
The angle rotated by the string before it becomes slack is given by:
The angle rotated by the string before it becomes slack is 2π3 radians.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Question for Short Answer16videos
WORK AND ENERGY
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Objective -28videos
WORK AND ENERGY
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer7videos
WAVE MOTION AND WAVES ON A STRING
Similar Questions
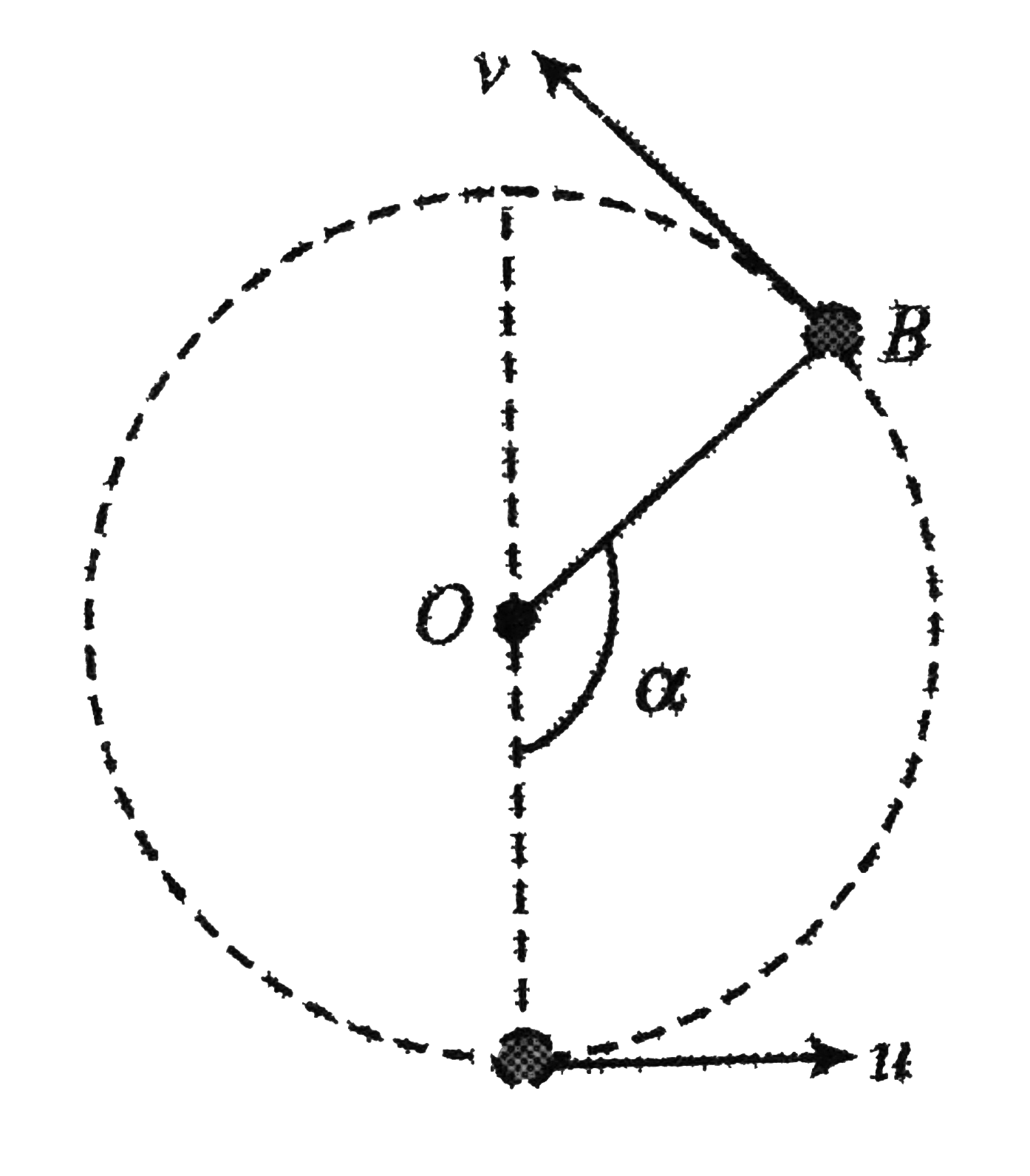
The bobo of a pendulum at rest is given a sharp hit to impart a horizontal velocity u where l is the length of the pendulum. Find the angle rotated by the string before it becomes slack.
View SolutionThe bob of a pendulum at rest is given a sharp hit to impart a horizontal velocity √10gl where l is the length of the pendulum. Find the tension in the string when a. the string is horizontal. B. The bob is at its highest point and c. the string makes an angle of 600 with the upward vertical.
View SolutionThe bob of pendulum is project with horizontal velocity of √3gf I is the length of string. Find the angular displacement of string before it becomes slack.
View SolutionA heavy particle is usspended by a 1.5 m long string . It is given a horizontal velocityof √57ms. a. Find the angle made by the string with the upward vertical, when it becomes slack. B. Find the speed of the particle at this instant. c.Find the maximum height reached by the particle over the point of suspension. Take g=10ms2
View SolutionA particle rests on the top of a smooth hemisphere of radius r. It is imparted a horizontal velocity of √ηgr. Find the angle made by the radius vector joining the particle with the vertical at the instant the particle losses contact with the sphere.
View SolutionA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl
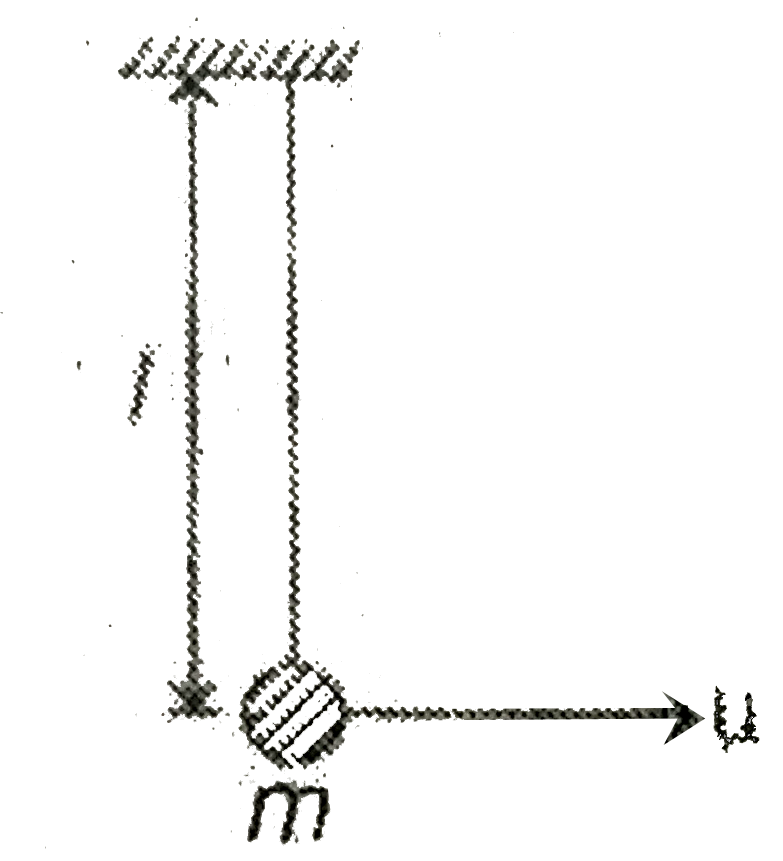
The maximum angle made by the string with downward vertical isView SolutionA particle is suspended by a light vertical inelastic string of length 1 from a fixed support. At its equilbrium position it is projected horizontally with a speed √6gl. Find the ratio of the tension in the string in its horizontal position to that in the string when the particle is vertically above the point of support.
View SolutionA simple pendulum is suspended from the ceiling of a car taking a turn of radius 10 m at a speed of 36 km/h. Find the angle made by the string of the pendulum with the vertical if this angle does not change during the turn. Take g=10ms2.
View SolutionBob B of the pendulum AB is given an initial velocity √3Lg in horizontal direction. Final the maximum height of the bob from the starting point,
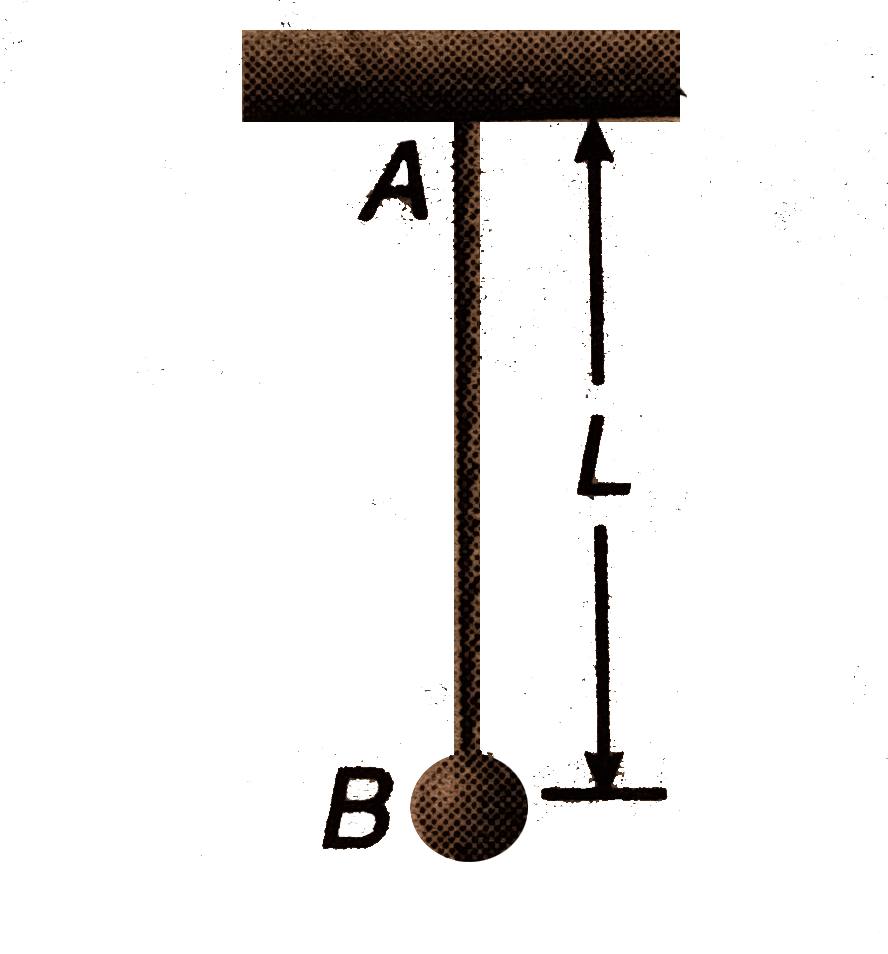
(a) if AB is a massless rod,
(b) if AB is a massless staring.View SolutionA heavy particle hanging from a string of length I is projected horizontally with speed √gl . Find the speed of the particle at the point where the tension in the string equals weight of the particle.
View Solution