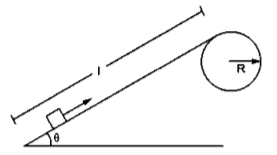
Figure shows a smooth track which consists of a straight inclined part of length l joining smoothly with the circular part. A particle of mass m is projected up the incline from its bottom. a.Find the minimum projected speed v0 for which the particle reaches the top of the track. b. Assuming that the projection speed is 2v0 and that the block does not lose contact with the track before reading its top, find teh force acting on it whenit reaches the top. c. Assuming that teh projection speed is only slightly greater than v0 where will the block lose contact with the track?
The correct Answer is:A, B, C, D
a. Net force on the particle A and B, F=mgsinθ
work done to reach B,
W=FS=mgsinθl
Again work done to reach B to C
=mgh
=mghR(1−cosθ)
So,→talworkdo≠<br>=mg(lsintheta+r(1-costheta)]<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/HCV_VOL1_C08_E01_099_S01.pngwh=80%mx-autosty≤=background:white;><br>Now,chan≥∈K.E.<br>=workdo≠<br>rarr 1/2mv_2^2=mg[lsintheta+R(1-costheta)]<br>rarr v_2=sqrt(2g[R(1-costheta)+lsintheta]<br>b.Whentehblockisprojectedataspeed2v_0<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/HCV_VOL1_C08_E01_100_S01.pngwh=80%mx-autosty≤=background:white;><br>LetthevelocityofCwillbev_0.<br>Apply∈ge≠rgyypricip≤<br>(1/2)mv_0^2 -(1/2)m(2v_0)^2<br>=−mg[lsinθ+R(1−cosθ)]
rarr V^2=4v_0^2-2g[lsintheta+R(1-costheta)]<br>=4.2g[lsintheta+R(1-costheta)]- 2g[lsintheta+R(1-costeta)]<br>soforceact∈gontehbody<br>rarr N=V^2/R=6mg[(l/R)sintheta+1-costheta]<br>c.Letthel∞secontactaftermak∈gan∠theta<br>(mv^2)/R=mgcostheta<br>rarr v^2=Rgcostheta.......i<br>Again 12mv2=mg(R−Rcosθ)
→v2=2gR(1−cosθ).........ii
Formiandiicostheta =2/3
→θ=cos−1(23)
Topper's Solved these Questions
- WORK AND ENERGYBOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Question for Short Answer
16 Videos
- WORK AND ENERGYBOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Objective -2
8 Videos
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer
7 Videos
Similar Questions
A particle of mass m is projected upword with velocity v=ve2 (ve) escape of the particle is
View SolutionA particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle is projected in gravity with a speed v0. Using W-E theorem, find the speed of the particle as the function of vertical distance y.
View SolutionA particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .
.
View SolutionA particle is projected along an inclined plane as shown in figure. What is the speed of the particle when it collides at point A ? (g=10ms2)

View SolutionA uniform magnetic field ¯¯¯B=B0ˆj exists in a space. A particle of mass m and charge q is projected towards negative x-axis with speed v from the a point (d,0,0) The maximum value v for which the particle does not hit y−z plane is .
View SolutionIn the figure shown, a particle is released from the position A on a smooth track. When the particle reaches at B, then normal reaction on it by the track. When the particle reaches at B, then normal reaction on it by the track is
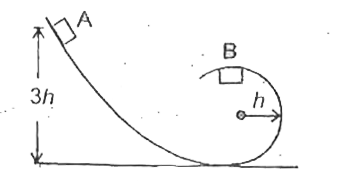
View SolutionA particle of mass m1 is projected to the right with speed v1 onto a smooth wedge of mass m2 which is simulateoulsy projected due the left with a speed v2. If the particle attains the highest point of the wedge, find h.

View SolutionA small particle of mass m is projected at an angle 0 with the x- axis, with initial velocity V0 in the x - y plane. Just before time 2V0sin0g ,the angular momentum of the particle about the point of projection is
_PHY_220_Q01.png)
View Solution
