A particle is projected in gravity with a speed v0. Using W-E theorem, find the speed of the particle as the function of vertical distance y.
To find the speed of a particle projected upwards in a gravitational field as a function of vertical distance y using the Work-Energy theorem, we can follow these steps:
1. Identify Initial Conditions:
- The particle is projected with an initial speed v0 at ground level (let's say at height y=0).
- The particle moves upward against gravity.
2. Define Forces and Work Done:
- The only force acting on the particle in the vertical direction is gravity, which does negative work as the particle moves upward.
- The work done by gravity when the particle moves a vertical distance y is given by:
W=−mgy
where m is the mass of the particle and g is the acceleration due to gravity.
3. Apply Work-Energy Theorem:
- The Work-Energy theorem states that the work done on an object is equal to the change in its kinetic energy:
W=ΔKE=KEfinal−KEinitial
- The initial kinetic energy KEinitial when the particle is at height y=0 is:
KEinitial=12mv20
- The final kinetic energy KEfinal when the particle is at height y is:
KEfinal=12mv2
where v is the speed of the particle at height y.
4. Set Up the Equation:
- Substituting the expressions for work and kinetic energy into the Work-Energy theorem:
−mgy=12mv2−12mv20
5. Simplify the Equation:
- Cancel out the mass m from both sides (assuming m≠0):
−gy=12v2−12v20
- Rearranging gives:
12v2=12v20−gy
- Multiply through by 2:
v2=v20−2gy
6. Solve for Speed:
- Taking the square root to find the speed v:
v=√v20−2gy
Final Result
The speed of the particle as a function of vertical distance y is given by:
v=√v20−2gy
- The particle is projected with an initial speed v0 at ground level (let's say at height y=0).
- The particle moves upward against gravity.
- The only force acting on the particle in the vertical direction is gravity, which does negative work as the particle moves upward.
- The work done by gravity when the particle moves a vertical distance y is given by:
W=−mgy
where m is the mass of the particle and g is the acceleration due to gravity.
- The Work-Energy theorem states that the work done on an object is equal to the change in its kinetic energy:
W=ΔKE=KEfinal−KEinitial
- The initial kinetic energy KEinitial when the particle is at height y=0 is:
KEinitial=12mv20
- The final kinetic energy KEfinal when the particle is at height y is:
KEfinal=12mv2
where v is the speed of the particle at height y.
- Substituting the expressions for work and kinetic energy into the Work-Energy theorem:
−mgy=12mv2−12mv20
- Cancel out the mass m from both sides (assuming m≠0):
−gy=12v2−12v20
- Rearranging gives:
12v2=12v20−gy
- Multiply through by 2:
v2=v20−2gy
- Taking the square root to find the speed v:
v=√v20−2gy
The speed of the particle as a function of vertical distance y is given by:
v=√v20−2gy
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Exercise 8.3
Explore 26 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Exercise 8.4
Explore 16 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Exercise 8.1
Explore 25 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
A heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizonally with speed √gl . Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.
View SolutionA particle is projected at an angle θ with an initial speed u.
View SolutionA particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .
.
View SolutionA particle is projected vertically upwards in vacuum with a speed u.
View SolutionTwo particles A and B are projected simultaneously from a fixed point of the ground. Particle A is projected on a smooth horizontal surface with speed v, while particle B is projected in air with speed v, while particle B is projected in air with speed 2v√3. If particle B hits the particle A, the angle of projection of B with the vertical is
View SolutionA particle is projected with a speed v0=√gR. The coefficient of friction the particle and the hemi- spherical plane is μ=0.5 Then , the acceleration of the partical is
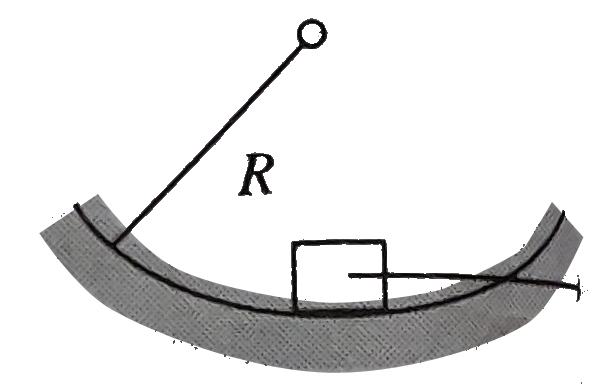
View SolutionA particle is projected horizontally with speed u from point A, which is 10 above the ground . If the particle hits the inclined perpendicularly at point B. [ g =10m/s2]
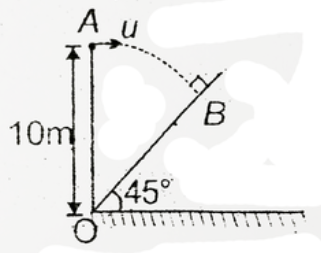
Find horizontal speed with which the particle was projected
View SolutionA heavy particle hanging from a string of length I is projected horizontally with speed √gl . Find the speed of the particle at the point where the tension in the string equals weight of the particle.
View SolutionA table with smooth horiztonal surface is truning at an angular speed ω abouyt its axis. A groove is made on the surface along a radius and a particle is gently placed inside the groove at a distance a from the centre. Find the speed of the speed of the particle as its distance from teh centre becomes L.
View Solution

