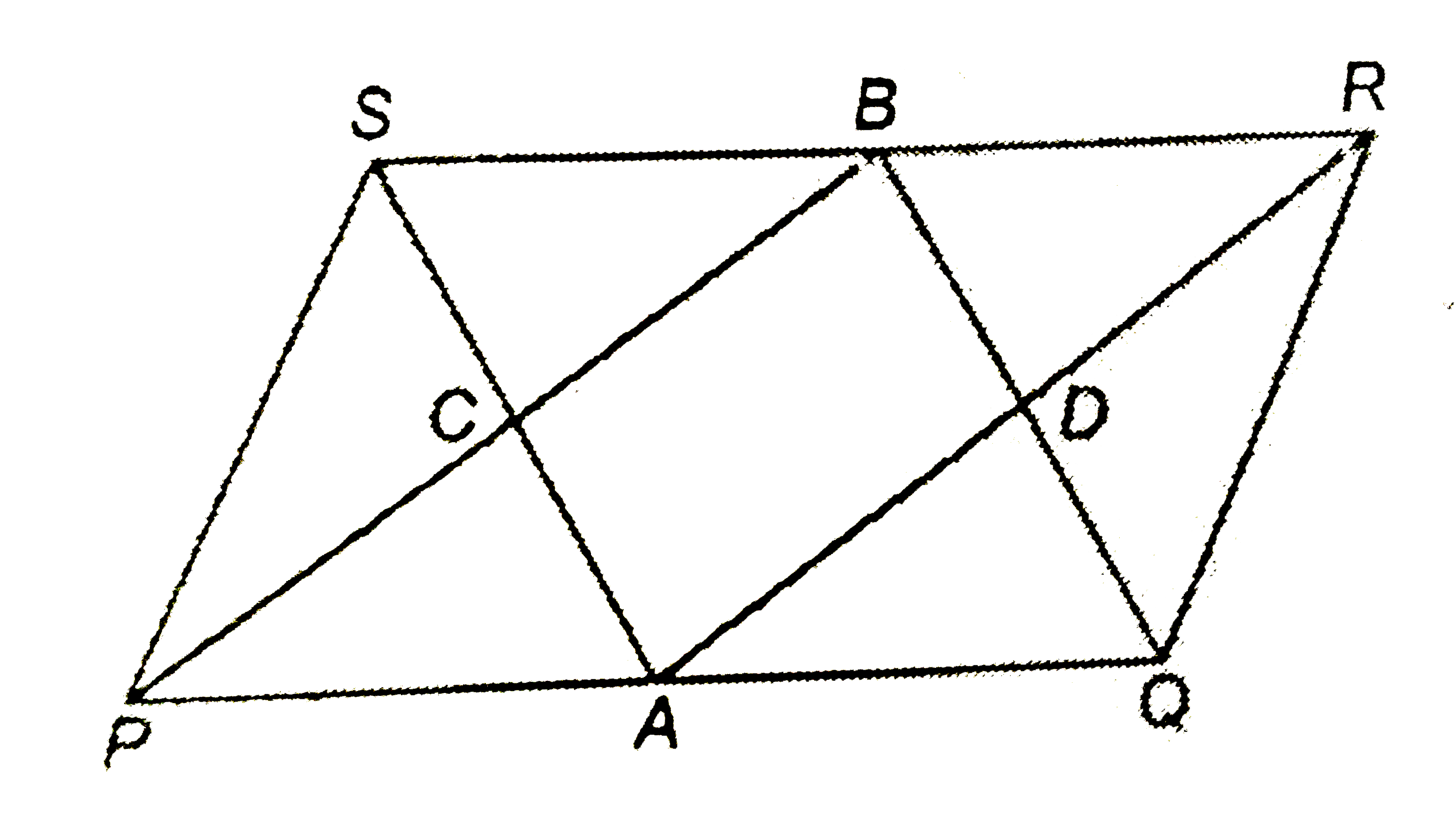
In the given figures, if PQRS is a parallelogram and AB||PS, then prove that OC||SR.
To prove that OC∥SR given that PQRS is a parallelogram and AB∥PS, we can follow these steps:
1. Identify the Triangles:
We will consider triangles OPS and OAB.
2. Use the Given Information:
Since AB∥PS, we know that corresponding angles are equal. Therefore, we have:
∠POS=∠OAB(common angle)
3. Establish Corresponding Angles:
From the parallel lines, we can also state:
∠OSP=∠OBA(corresponding angles)
4. Apply Angle-Angle (AA) Criterion:
Since we have two pairs of equal angles, we can conclude that:
△OPS∼△OAB(by AA criterion)
5. Set Up the Proportionality:
From the similarity of the triangles, we have:
PSAB=OSOB
This can be labeled as equation (1).
6. Consider Another Set of Triangles:
Now, consider triangles CAB and CQR.
7. Use the Properties of the Parallelogram:
Since PQRS is a parallelogram, we know:
PS∥QRandAB∥PS
Therefore, we can conclude:
AB∥QR
8. Establish Corresponding Angles Again:
From the parallel lines, we can state:
∠ACB=∠QCR(common angle)
And:
∠CAB=∠CQR(corresponding angles)
9. Apply Angle-Angle (AA) Criterion Again:
Thus, we can conclude:
△CAB∼△CQR(by AA criterion)
10. Set Up the Proportionality for the Second Pair:
From the similarity of these triangles, we have:
ABQR=CBCR
This can be labeled as equation (2).
11. Relate the Proportions:
Since QR=PS in parallelogram PQRS, we can replace QR with PS in equation (2):
ABPS=CBCR
12. Combine the Proportions:
Now we have two equations:
- From (1): PSAB=OSOB
- From (2): ABPS=CBCR
Setting these equal gives us:
OSOB=CBCR
13. Cross-Multiply:
Cross-multiplying gives:
OS⋅CR=OB⋅CB
14. Apply the Converse of Basic Proportionality Theorem:
According to the converse of the basic proportionality theorem, if a line divides two sides of a triangle in equal ratios, then it is parallel to the third side. Here, since BSOS=BRCR, we conclude:
OC∥SR
15. Final Conclusion:
Therefore, we have proved that:
OC∥SR
Hence, proved.
We will consider triangles OPS and OAB.
Since AB∥PS, we know that corresponding angles are equal. Therefore, we have:
∠POS=∠OAB(common angle)
From the parallel lines, we can also state:
∠OSP=∠OBA(corresponding angles)
Since we have two pairs of equal angles, we can conclude that:
△OPS∼△OAB(by AA criterion)
From the similarity of the triangles, we have:
PSAB=OSOB
This can be labeled as equation (1).
Now, consider triangles CAB and CQR.
Since PQRS is a parallelogram, we know:
PS∥QRandAB∥PS
Therefore, we can conclude:
AB∥QR
From the parallel lines, we can state:
∠ACB=∠QCR(common angle)
And:
∠CAB=∠CQR(corresponding angles)
Thus, we can conclude:
△CAB∼△CQR(by AA criterion)
From the similarity of these triangles, we have:
ABQR=CBCR
This can be labeled as equation (2).
Since QR=PS in parallelogram PQRS, we can replace QR with PS in equation (2):
ABPS=CBCR
Now we have two equations:
- From (1): PSAB=OSOB
- From (2): ABPS=CBCR
OSOB=CBCR
Cross-multiplying gives:
OS⋅CR=OB⋅CB
According to the converse of the basic proportionality theorem, if a line divides two sides of a triangle in equal ratios, then it is parallel to the third side. Here, since BSOS=BRCR, we conclude:
OC∥SR
Therefore, we have proved that:
OC∥SR
Hence, proved.
Topper's Solved these Questions
Similar Questions
Knowledge Check
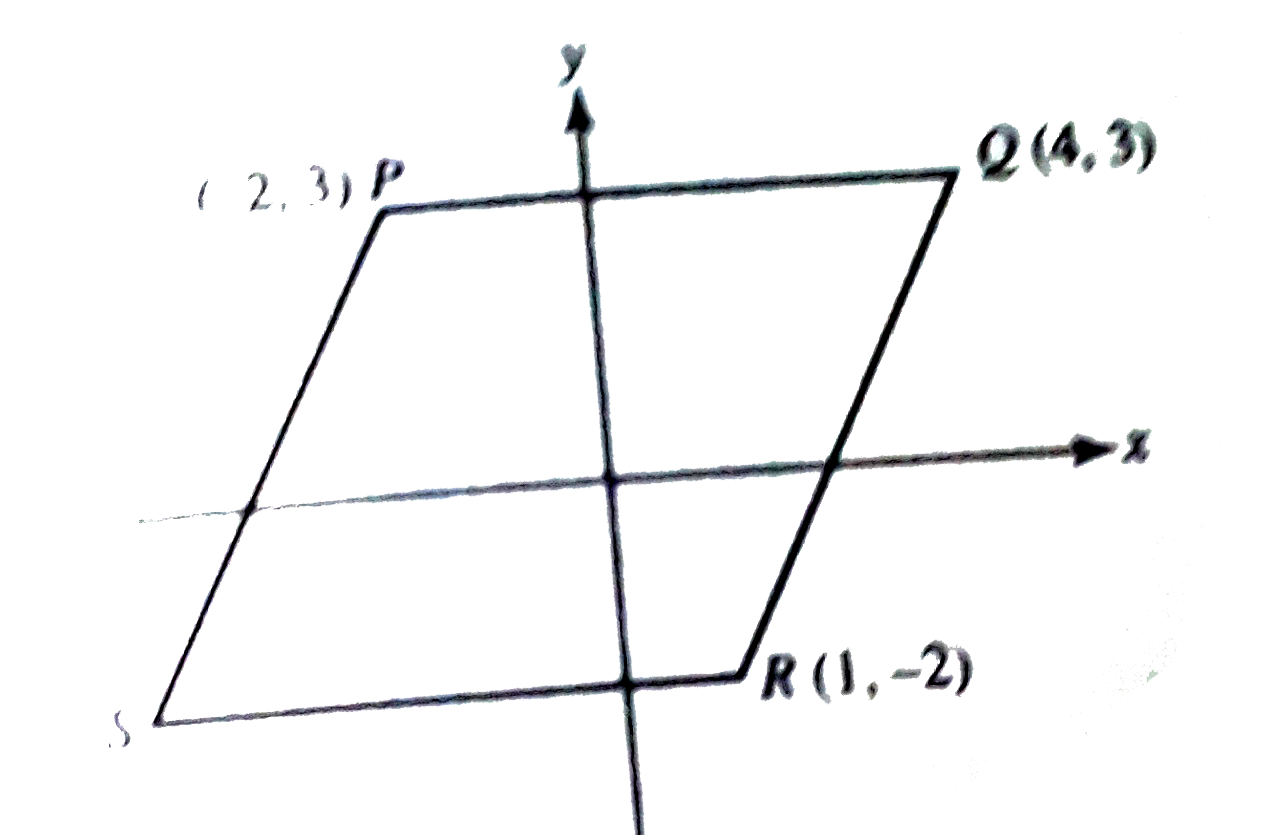
In the diagram above , PQRS is a parallelogram. What is the area of PQRS ?A15B18C30D3√34In the given figure, PQR is a straight line. Find the value of x
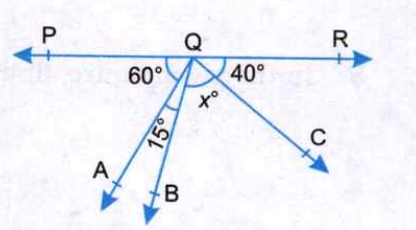 Ax=75∘Bx=35∘Cx=45∘Dx=65∘
Ax=75∘Bx=35∘Cx=45∘Dx=65∘
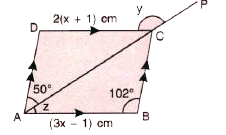
In the given figure, ABCD is a parallelogram. Find the values of x, y and z
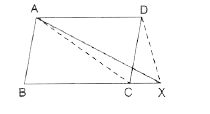
View SolutionIn the given figure, ABCD is a parallelogram BC is produced to point X. prove that :
area(ΔABX)=area( .ACXD)
View SolutionIn the given figure, □ABCD is a parallelogram. If DM ⊥ AC and BN ⊥ AC, then show that □BNDM is a parallelogram.

View SolutionIn the adjoining figure, PQRS is a parallelogram. A and B are the mid-points of PQ of SR respectively. If PS= BR, then prove that quadrilateral ADBC is a reactangle.
View SolutionIn the given figure, PQRS is a parallelogram. If X and Y are mid-point of PQ and SR respectively and diagonal SQ is joined. Find the ratio of area of (∣∣gmXQRY): area (ΔQSR)
View SolutionIn the given figure PQRS is an isosceles trapezium, fixd x and y.

View Solution



