In the given figure, □ABCD is a parallelogram. If DM ⊥ AC and BN ⊥ AC, then show that □BNDM is a parallelogram.

InΔADMandΔCBN,
∵⎧⎪⎨⎪⎩AD=CB(opposite sides of parallelogram)∠AMD=∠CNB(each90∘)∠DMA=∠BCA(alternate interior angles)
∴ΔADM≅ΔΔCBA (AAS therem)
Again, in ΔCDNandΔABM, (c.p.c.t)
Again, in ΔCDNandΔABN,
∵⎧⎪⎨⎪⎩CD=AB(opposite sides of a parallelogram)∠DCN=∠BAM(alternate interior angles)∠CN=AM(proved above)
∴ΔCDN≅ΔABM (SAS theorem)
⇒DN=BM (c.p.c.t)
Now, DM= BN and DN = BM
⇒□BNDMis a parallelogram. (∵pairs of opposite sides are equal)
Alternative Method :
Construction : Join BD which intersect AC at O.
Proof : In ΔADMandΔCBN,
∵⎧⎪⎨⎪⎩AD=CB(opposite sides of a parallelogram)∠AMD=∠CNB(each90∘)∠DAM=∠BCN(alternate interior angles)
∴ΔADM≅ΔCBN (AAS)
∴AM=CN ...(1)(c.p.c.t)
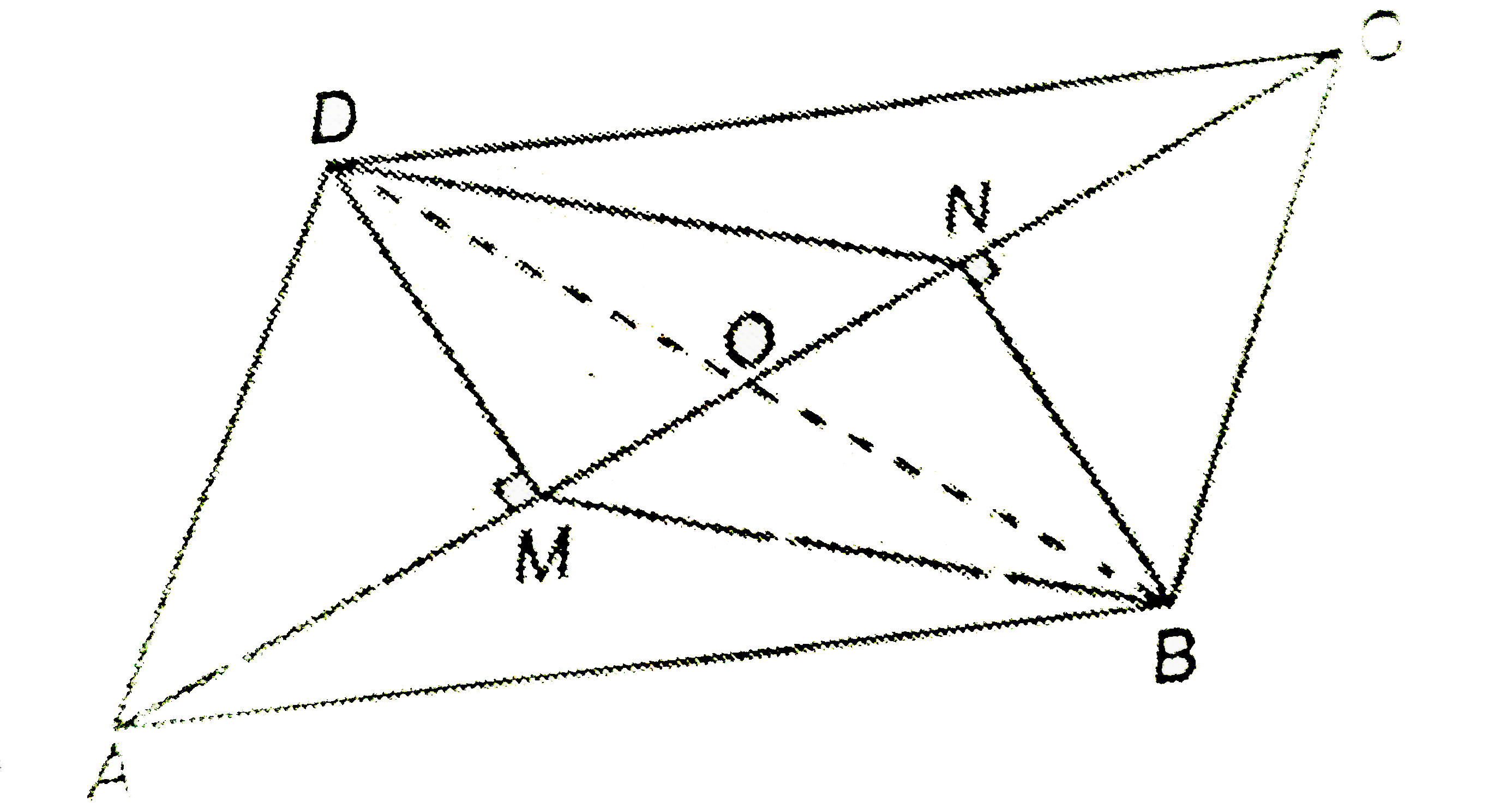
But since □ABCD is a parallelogram
∴AO=OC....(2)andDO=OB....(3)} (diagonals of a parallelogram bisect each other)
Substacting (1) from (2), we get
AO- AM = OC - CN
⇒ OM=ON ...(4)
Now, from (3) and (4), we can say that diagonals of a quadrilateral BNDM bisect each other.
Hence □BNDM is a parallelogram.
Topper's Solved these Questions
- QUADRILATERALSBook:NAGEEN PRAKASHAN ENGLISHChapter:QUADRILATERALSExercise:Problems From NCERT/exemplar
Explore 11 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHAN ENGLISHChapter:QUADRILATERALSExercise:Exercise 8a
Explore 29 Videos
- PROBABILITYBook:NAGEEN PRAKASHAN ENGLISHChapter:PROBABILITYExercise:Revision Exercise (very Short Answer /short Answer Questions)
Explore 10 Videos
- STATISTICSBook:NAGEEN PRAKASHAN ENGLISHChapter:STATISTICSExercise:Revision Exercise
Explore 12 Videos
Similar Questions
Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
View SolutionThe angles of a quadrilateral are 89∘and113∘ If the other two angles are equal, find the equal angles.
View SolutionWhat is the probability of an impossible event?
View SolutionIf the heights of 5 persons are 140 cm, 150 cm, 152 cm, 158 cm and 161 cm respectively, find the mean height.
View SolutionIn the given figure, □ABCD is a parallelogram. If DM ⊥ AC and BN ⊥ AC, then show that □BNDM is a parallelogram.

View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of figure given below.
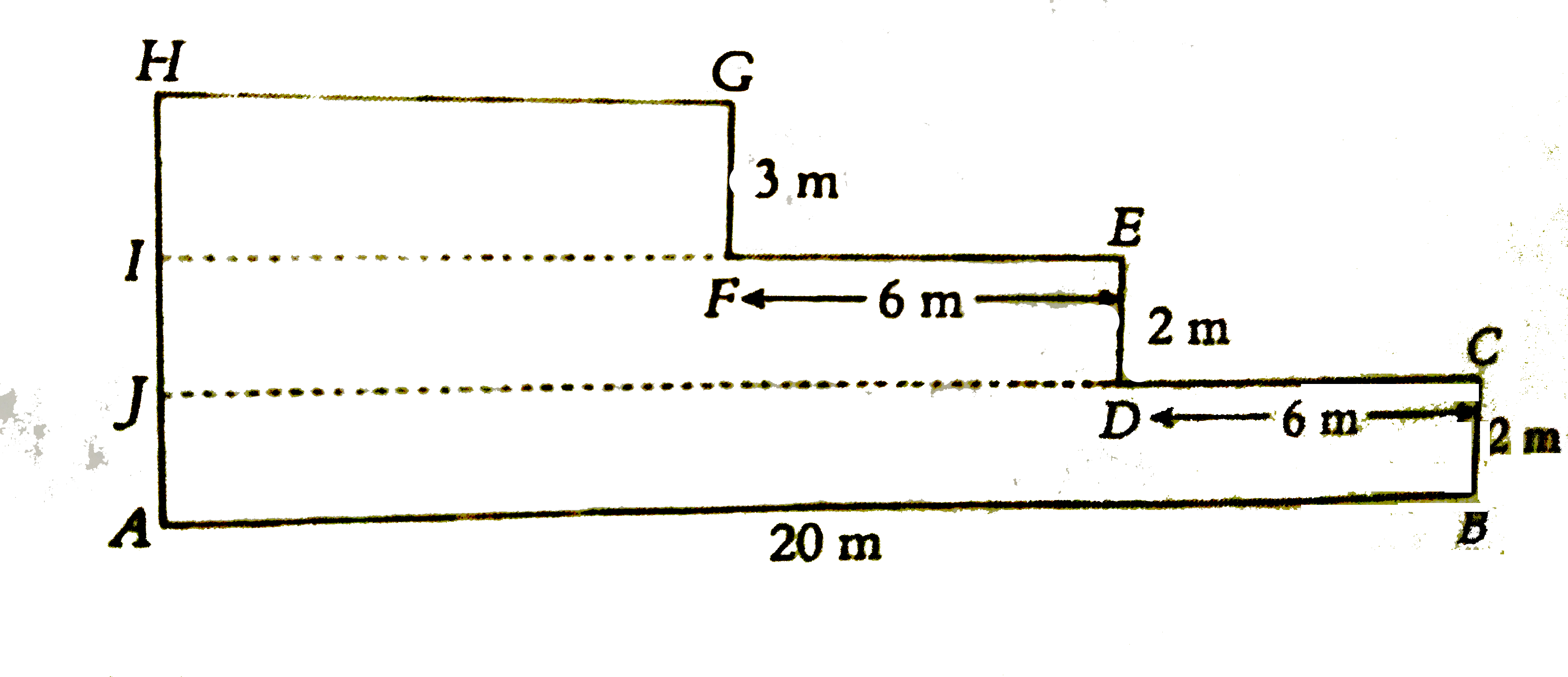
View SolutionFind the perimeter of the figure given below.
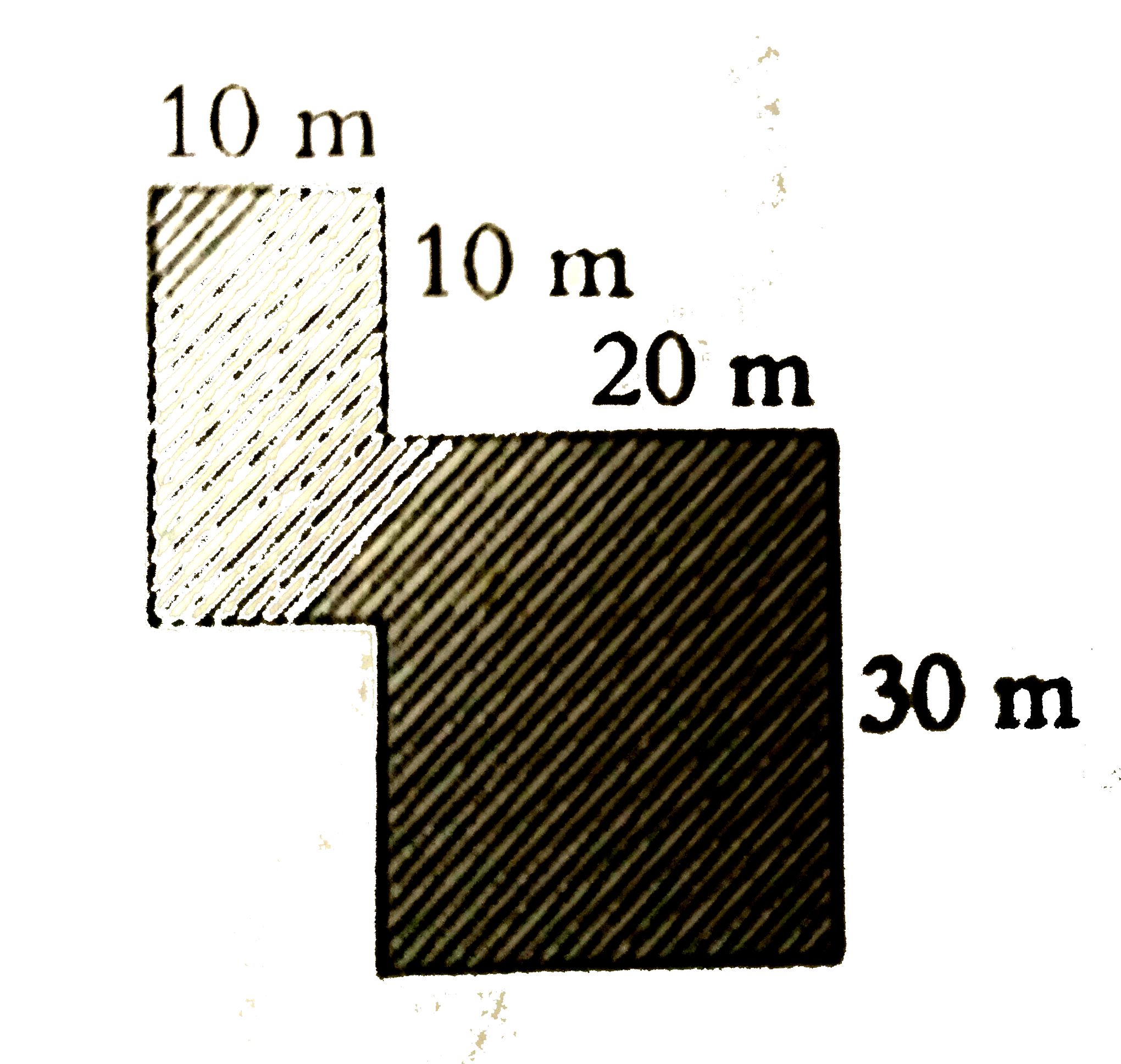
View SolutionFind the area of the figure given below.

View SolutionThe area of the shaded part in the figure given below is ______.

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View Solution