Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle

Video Solution

Text Solution

Verified by Experts

Let ABC be a right triangle, right angled at B and AB=y,BC=x
Three semi-circles are drawn on the sides AB, BC and AC, respectively with diameters AB,BC and AC respectively.
Again, let area of circles with diametersAb,BC and Acare respectively $A_{1}, A_{2} and A_{3}$
To prove $A_{3} = A_{1} + A_{2}$
Proof In $Δ A B C$ by pythogoras theorem,
$A C^{2} = A B^{2} + B C^{2}$
$\Rightarrow A C^{2} + y^{2} + x^{2}$
$\Rightarrow A C = \sqrt{y^{2} + x^{2}}$
we know that, area of semi circle with radius, r $= \frac{π r^{2}}{2}$
$∴$ Area of semicircle drawn on AC, $A_{3} = \frac{π}{2} {(\frac{A C}{2})}^{2} = \frac{π}{2} {(\frac{\sqrt{y^{2} + x^{2}}}{2})}^{2}$
$\Rightarrow A_{3} = \frac{π (y^{2} + x^{2})}{8}$ ...(i)
Now, areea of semi circle drawn on AB, $A_{1} = \frac{π}{2} {(\frac{A B}{2})}^{2}$
$\Rightarrow A_{1} = \frac{π}{2} {(\frac{y}{2})}^{2} \Rightarrow A_{1} = \frac{π y^{2}}{8}$ ...(ii)
and area of semi-circle drawn on BC, $A_{2} = \frac{π}{2} {(\frac{B C}{2})}^{2} = \frac{π}{2} {(\frac{x}{2})}^{2}$
$\Rightarrow A_{2} = \frac{π x^{2}}{8}$
On adding Eqs. (ii) and (iii), we get $A_{1} + A_{2} = \frac{π y^{2}}{8} + \frac{π x^{2}}{8}$
$= \frac{π (y^{2} + x^{2})}{8} = A_{3}$ [from Eq.(i)]
$\Rightarrow A_{1} + A_{2} = A_{3}$ Hence proved

Updated on:21/07/2023

|

Class 10 MATHS TRIANGLES

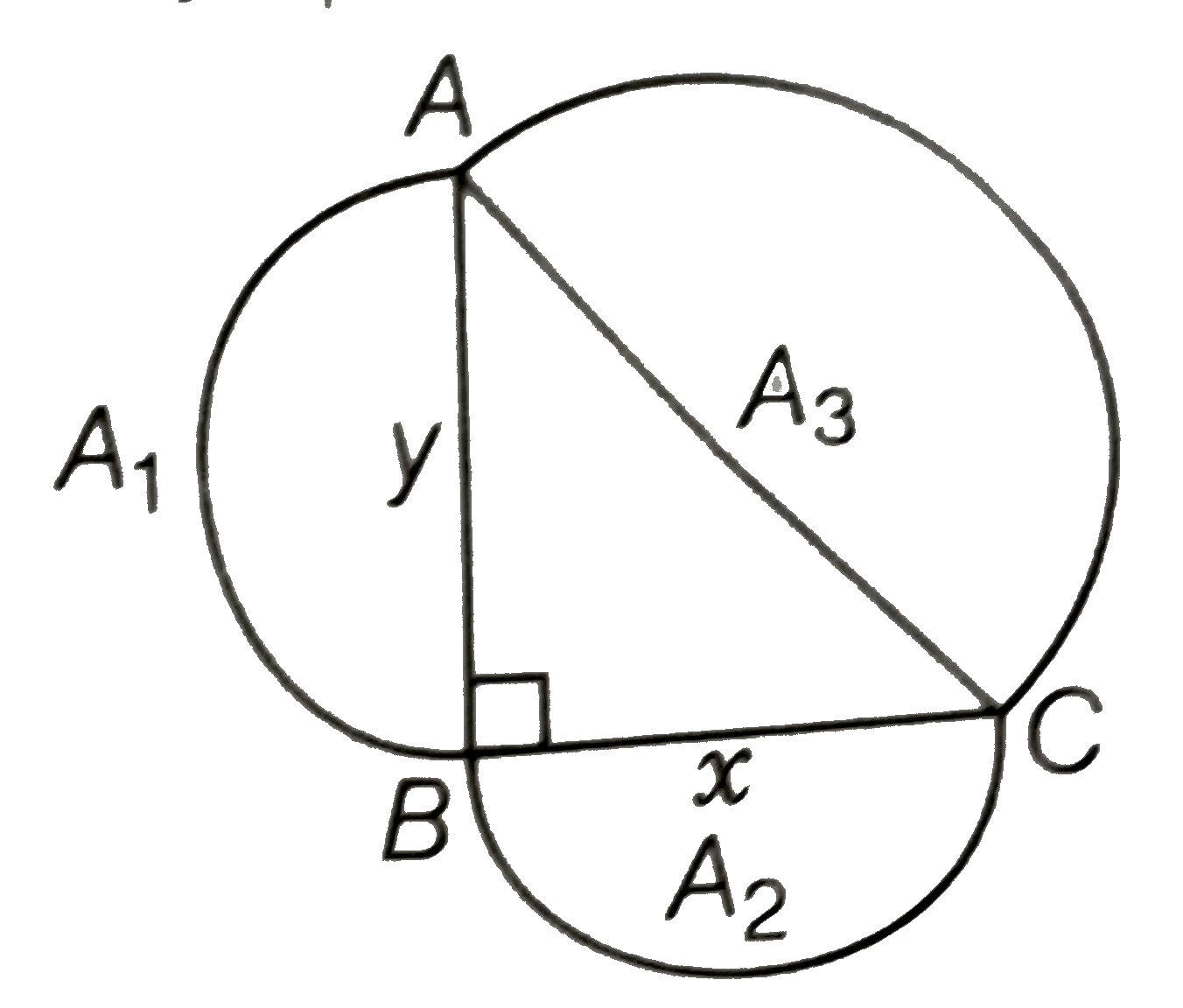
Topper's Solved these Questions

Similar Questions

NCERT EXEMPLAR ENGLISH-TRIANGLES-Long Answer Type Questions

Home
Ask Doubt
Profile