In given figure,l||m and liner segments AB, CD and EF are concurrent at point P. Prove that AEBF=ACBD=CEFD
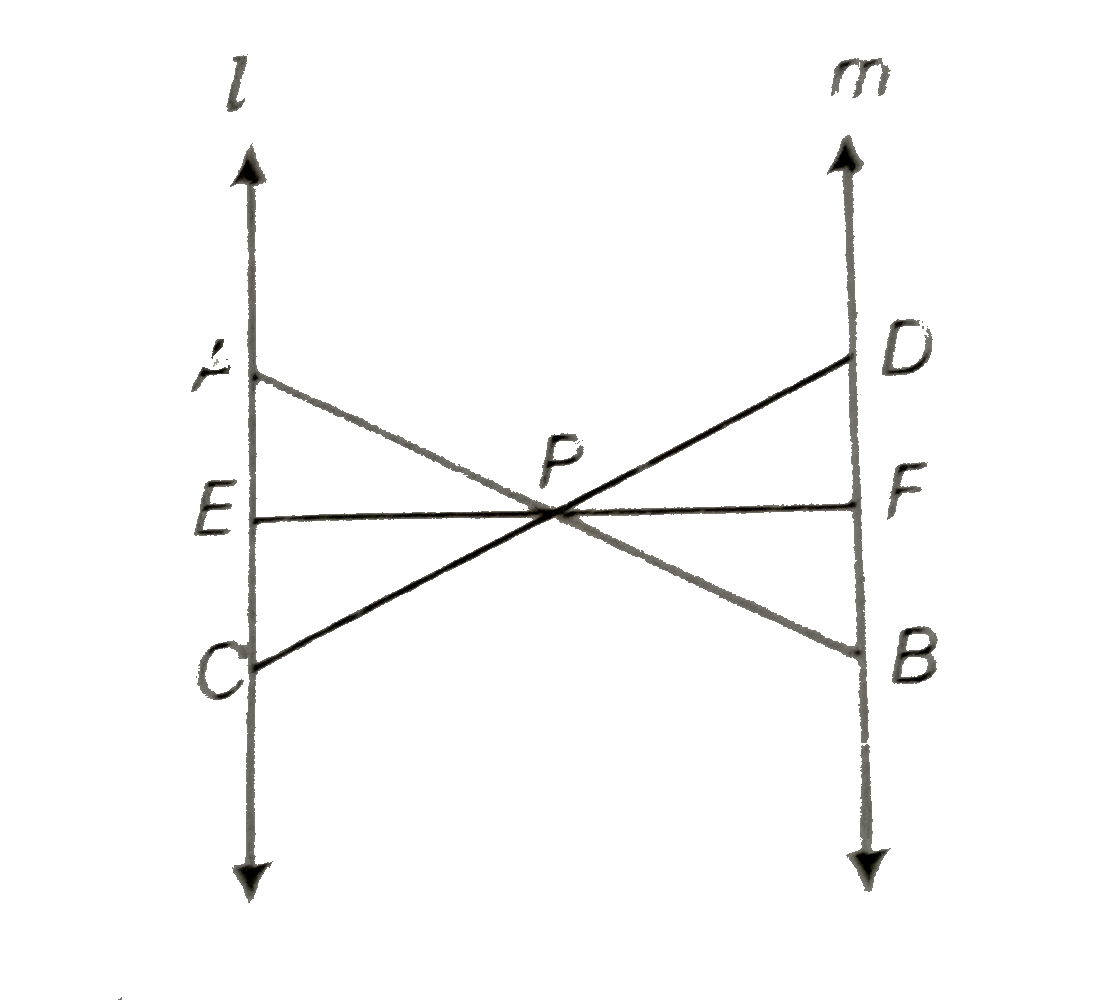
Given l||m and line segments AB, CD and EF are concurrent at point P
To prove AEBF=ACBD=CEFD
Proof In ΔAPCandΔBPD,∠APC=∠BPD [vertically opposite angle]
∠PAC=∠PBD [alternate angle]
∴ΔAPC~ΔBPD [by AAA similarity criterion]
Then, APPB=ACBD=PCPD
In ΔAPE and ΔBPF,∠APE=∠BPF [vertically opposite angles]
∠PAE=∠PBF [alternate angles]
∴ΔAPE~ΔBPF [by AAA similarity criterion]
Then, APPB=AEBF=PEPF....(ii)
In ΔPECandΔPFD,∠EPC=∠FPD [vertically opposite angle]
∠PCE=∠PDF [alternate angles]
∴ΔPEC~ΔPFD [by AAA similarity criterion]
Then, PEPF=PCPD=ECFD....(iii)
From Eqs. (i) ,(ii) and (iii),
APPB=ACBD=AEBF=PEPF=ECFD
∴AEBF=ACBD=CEFD Hence proved
Topper's Solved these Questions
Similar Questions
In the adjoining figure, common tangents AB and CD to two circles intersect at P.
Prove that AB=CD.

View SolutionIn the given figures, AB > AC and D is any point on BC.
Prove that : AB >AD.
View SolutionIn the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a) AB+BC+CD+DA<2(AC+BD)
(b) AB+BC+CD+DA>(AC+BD)

View SolutionIn the given figure, DE||ACandDF||AE.
Prove that BFFE=BEEC

View SolutionIn the given figure, DE||ACandDF||AE.
Prove that BFFE=BEEC

View SolutionIn triangle ABC, AB=AC and BD is perpendicular to AC. Prove that : BD2−CD2=2CD×AD
View SolutionIn the given figure, lines l and m are parallel. Three concurrent lines through point O meet line l at points A, B and C, and line m at points P, Q and R as shown. Prove that : ABBC=QRPQ

View SolutionABC is a triangle in which AB = AC and D is any point on BC. Prove that:
AB2−AD2=BD.CD
View SolutionIn an isosceles triangle ABC, AB = AC and D is a point on BC produced. Prove that :
AD2=AC2+BD.CD
View SolutionIn the given figure D is mid-point of AB. DE//BC and DF //AC . Prove that : DE = BF

View Solution
