O is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB||DC. Through O , aline segment PQ is drawn parallel to AB meeting AD in P and BC in Q, prove that PO=QO.
Given ABCD is a trapezium, Diagonals AC and BD are intersect at O .
PQ||AB||DC
To prove PO=QO
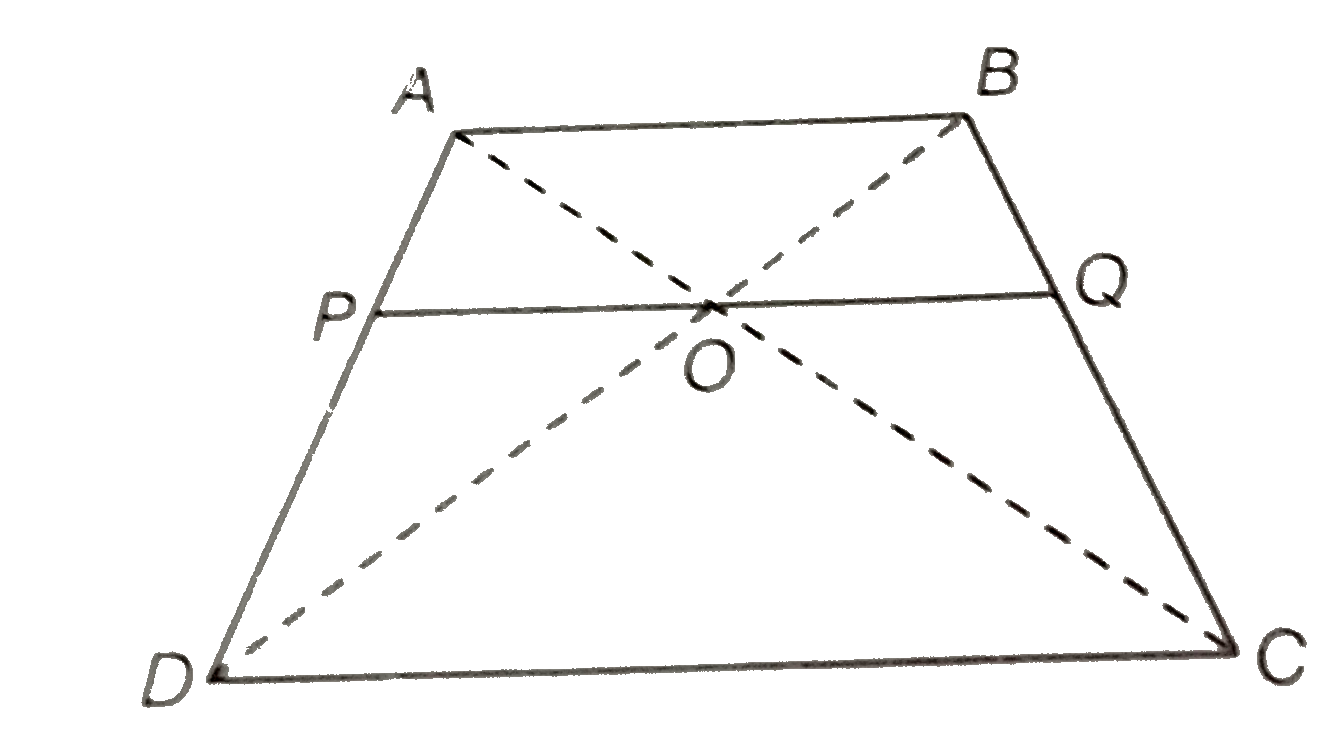
Proof in ΔABDandΔPOD,PO||AB [∵PQ||AB]
∠D=∠D [common angles]
∠ABD=∠POD [corresponding angles]
∴ΔABD~ΔPOD [by AAA similarity criterion]
Then, OPAB=PDAD...(i)
In ΔABCandΔOQC,OQ||AB [∵OQ||AB]
∠C=∠C [common angle]
∠BAC=∠QOC [corresponding angles]
∴ΔABC~ΔOQC [by AAA similarity criterion]
Then, OQAB=QCBC..(ii)
Now in ΔADCOP||DC
∴APPP=OAOC [by basic propertionality theorem]...(iii)
In ΔABC OQ||AB
∴BQQC=OAOC [by basic propertionality theorem]....(iv)
From Eqs. (iii) and (iv),
APPD=BQQC
Adding 1 on both sides, we get
APPD+1=BQQC+1
⇒AP+PDPD=BQ+QCQC
⇒ADPD=BCQC
⇒PDAD=QCBC
⇒OPAB=OQBC [from Eqs. (i) and (ii)]
⇒OPAB=OQAB [from Eq. (i)]
⇒OP=OQ Hence proved
Topper's Solved these Questions
Similar Questions
E is the mid-point of the side AD of the tarapezium ABCD with AB∣∣DC. A line through E drawn parallel to AB intersects BC at F. Show that F is the mid-points of BC.
View SolutionIn trapezium ABCD, AB∣∣DC and L is the mid-point of BC. Through L, a line PQ∣∣AD has been drawn which meets AB in P and DC produced in Q. Prove that ar (ABCD) = ar (APQD).

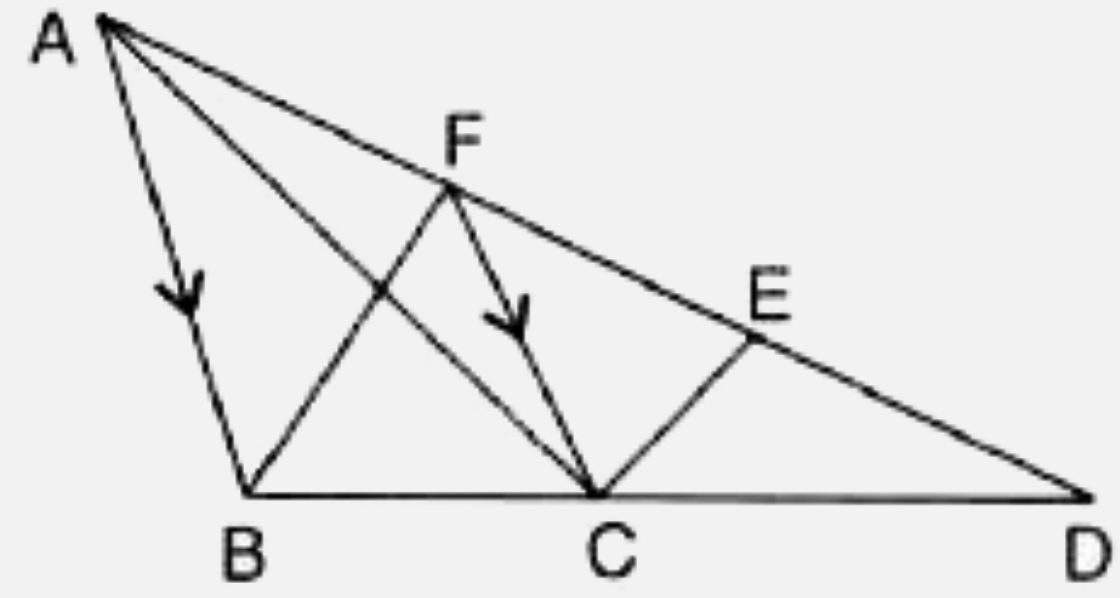
View SolutionIn the following figure, F and E are points on the side AD of the triangle ABD. Through F a line is drawn parallel to AB to meet BD at point C .
Prove that : ar (ΔACE)=ar (quad . BCEF )
View SolutionIn a trapezium ABCD, AB/DC, E is mid-point of aD. A line through E and parallel to AB intersects BC at point F. Show that:
2EF=AB+DC
View SolutionDiagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that OAOC=OBOD
View SolutionABCD is a trapezium with AB∣∣DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (ADX) = ar (ACY).
View SolutionABCD is a trapezium with AB parallel to DC. A line parallel to AC intersects AB at X and BC at Y. Prove that area of ΔADX = area of ΔACY.
View SolutionABCD is a trapezium with AB parallel to DC. A line parallel to AC intersects AB at X and BC at Y. Prove that area of ΔADX = area of ΔACY.
View SolutionThe diagonals of a trapezium ABCD with AB||DC intersect each other at point O. If AB = 2CD, find the ratio of the areas of triangle AOB and COD.
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that :
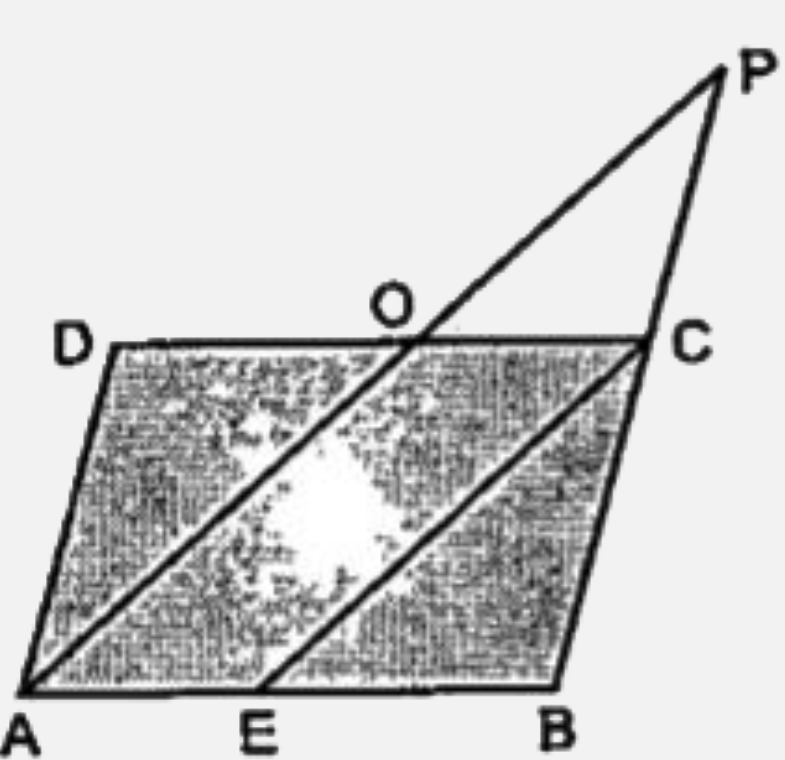
BP=2AD
View Solution

