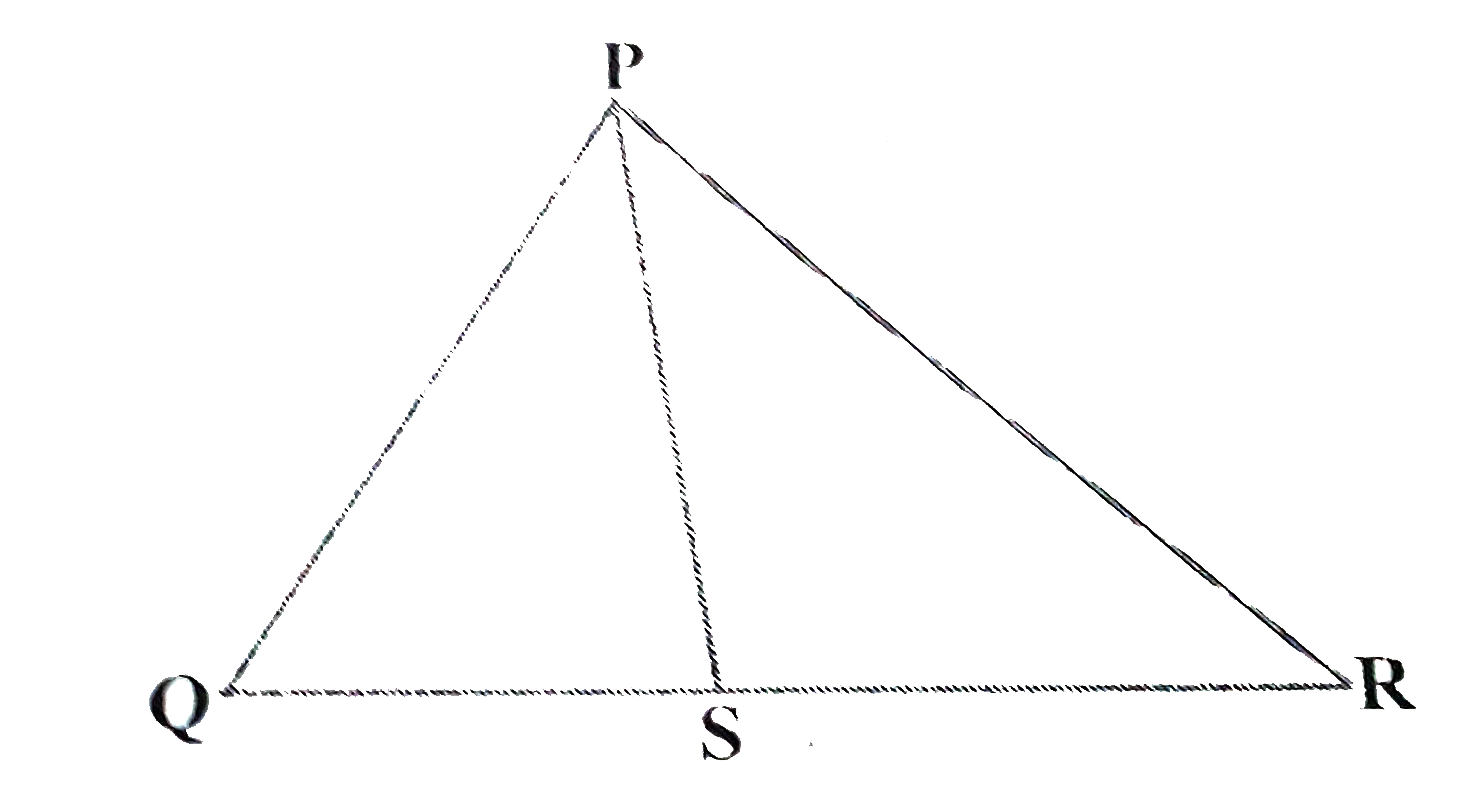
In PQR, QM⊥PR and PR2−PQ2=QR2 . Prove that QM2=PM×MR
To prove that QM2=PM×MR in triangle PQR where QM⊥PR and PR2−PQ2=QR2, we can follow these steps:
Step 1: Understand the Given Information
We have triangle PQR with QM being perpendicular to PR. This means that ∠QMR=90∘.
Step 2: Apply the Pythagorean Theorem
From the given information, we know that:
PR2−PQ2=QR2
We can rearrange this to express PR2:
PR2=QR2+PQ2
This indicates that triangle PQR satisfies the Pythagorean theorem.
Step 3: Identify Angles in the Triangles
Since QM⊥PR, we can say:
- ∠PQM=90∘
- ∠QMR=90∘
Step 4: Use Angle Relationships
Let:
- ∠PQM=θ
- ∠QMR=θ
Since ∠PQM+∠QMR+∠PRQ=180∘, we can derive relationships between the angles in triangles PQM and QMR.
Step 5: Establish Similarity of Triangles
From the angles, we can see that:
- △PQM∼△QMR (by AA criterion since they share ∠QM and both have a right angle).
Step 6: Set Up Proportions from Similar Triangles
From the similarity of triangles, we can write:
PQQR=QMMR=PMQM
Step 7: Cross-Multiply to Find QM2
From the proportion QMMR=PQQR, we can cross-multiply:
QM×QR=PQ×MR
Thus, squaring both sides gives:
QM2=PM×MR
Conclusion
We have shown that:
QM2=PM×MR
This completes the proof.
We have triangle PQR with QM being perpendicular to PR. This means that ∠QMR=90∘.
From the given information, we know that:
PR2−PQ2=QR2
We can rearrange this to express PR2:
PR2=QR2+PQ2
This indicates that triangle PQR satisfies the Pythagorean theorem.
Since QM⊥PR, we can say:
- ∠PQM=90∘
- ∠QMR=90∘
Let:
- ∠PQM=θ
- ∠QMR=θ
From the angles, we can see that:
- △PQM∼△QMR (by AA criterion since they share ∠QM and both have a right angle).
From the similarity of triangles, we can write:
PQQR=QMMR=PMQM
From the proportion QMMR=PQQR, we can cross-multiply:
QM×QR=PQ×MR
Thus, squaring both sides gives:
QM2=PM×MR
We have shown that:
QM2=PM×MR
This completes the proof.
Topper's Solved these Questions
- TRIANGLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Long Answer Type Questions
18 Videos
- TRIANGLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Very Short Answer Typw Questions
12 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS
20 Videos
Similar Questions
In Figure, it is given that LM=MN, QM=MR, ML ⊥PQ and MN ⊥PR. Prove that PQ=PR
View SolutionIf P + Q = R and P - Q = S, prove that R2+S2=2(P2+Q2)
View SolutionIn Figure, PS=QR and ∠SPQ=∠RQP. Prove that PQS ≅ QPR, PR=QS and ∠QPR= ∠PQS
View SolutionIn Fig 7.51, PR > PQand PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.

View SolutionIn figure PS is the bisector of ∠QPRof ΔPQR. Prove that QSSR=PQPR.
View SolutionIn Figure, PQRS is a quadrilateral and T and U are respectively points on PS and RS such that PQ=RQ, ∠PQT=∠RQU and ∠TQS=∠UQS. Prove that QT=QU.
View SolutionIn triangle PQR, if PQ=RQ and L, M and N are the mid-points of the sides PQ, QR and RP respectively. Prove that LN=MN.
View SolutionPQR is a triangle right-angled at P and M is a point on QR such that PM⊥QR. Show thatPM2=QM.MR.
View SolutionIn △PQR , M and N are points on sides PQ and PR respectively such that PM=15cm and NR=8cm . If PQ=25cm and PR=20cm state whether MN∣∣QR .
View SolutionIn Figure, ∠PQR= ∠PRQ, then prove that ∠PQS= ∠PRT.
View Solution
