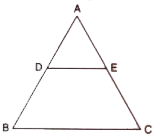
In figure, if DE||BC, then find the ratio of ar (ΔADE) and ar(DECB).
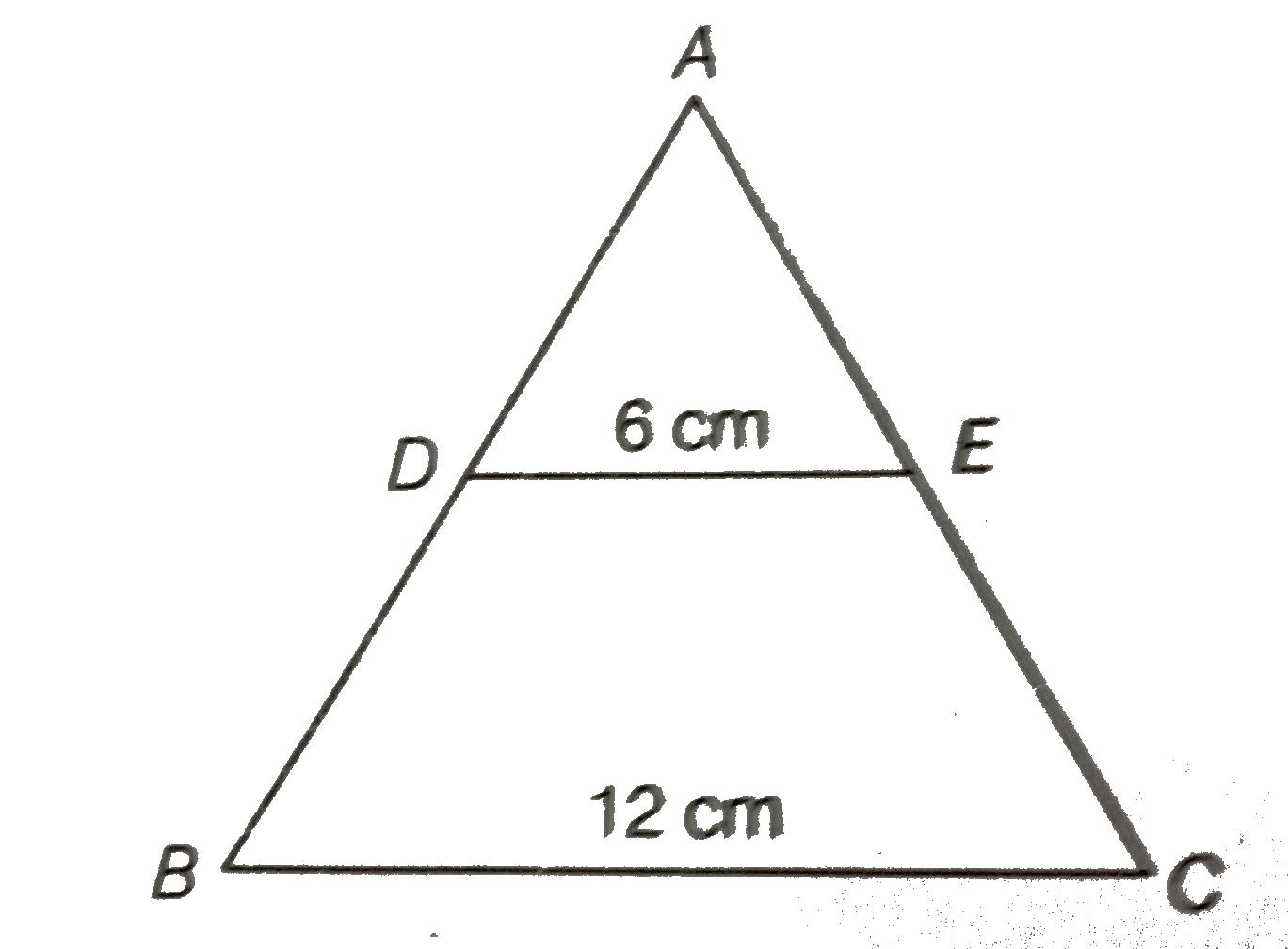
Given, DE||BC, DE= 6 cm and BC= 12 cm
In ΔADE,
∠ABC=∠(ADE) [corresponding angle]
∠ACB=∠AED [corresponding angle]
and ∠A=∠A [common sides]
∴ΔABC~ΔAED [by AAA similarity criterion]
Then, ar(ΔADE)ar(ΔABC)=(DE)2(BC)2
=(6)2(12)2=(12)2
⇒ar(ΔADE)ar(ΔABC)=(12)2=14
Let ar(ΔADE)=k,then ar(ΔABC)=4k
Now, ar(DECB)=ar(ABC)-ar(ADE)=4k-k=3k
∴ Required ratio=ar(ADE) : ar(DECB)=K : 3k=1 : 3
Topper's Solved these Questions
- TRIANGLESBook:NCERT EXEMPLAR ENGLISHChapter:TRIANGLESExercise:Long Answer Type Questions
Explore 18 Videos
- TRIANGLESBook:NCERT EXEMPLAR ENGLISHChapter:TRIANGLESExercise:Very Short Answer Typw Questions
Explore 12 Videos
- SURFACE AREAS AND VOLUMESBook:NCERT EXEMPLAR ENGLISHChapter:SURFACE AREAS AND VOLUMESExercise:LONG ANSWER TYPE QUESTIONS
Explore 20 Videos
Similar Questions
In the given figure if DE||BC, find the value of x.
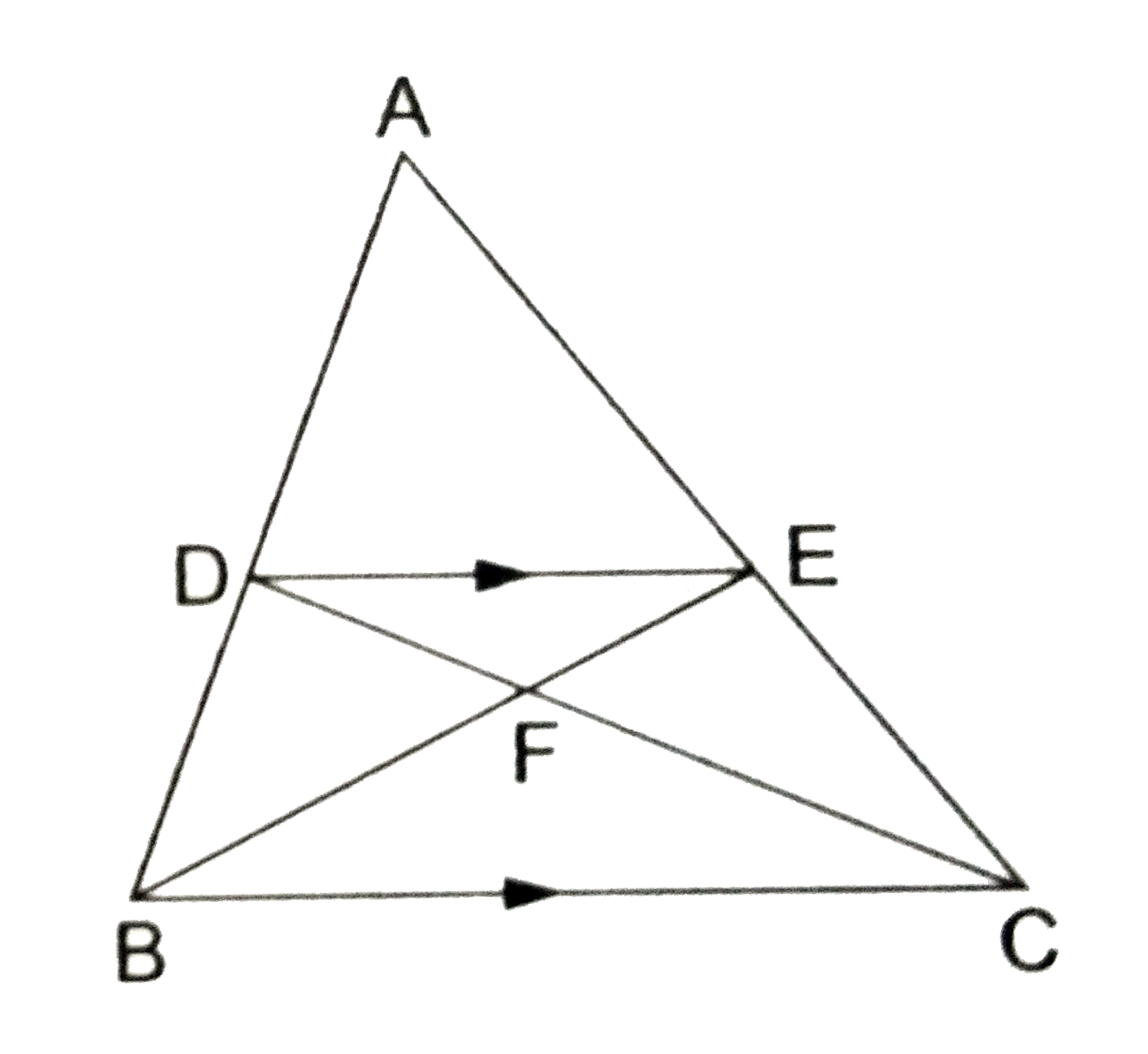
View SolutionIn the given figure DE∣∣BCandAD:DB=5:4
Find the ratio ar(ΔDEF):ar(ΔCFB)
View SolutionIn a trapezium ABCD, AB || DC, AB = a cm, and DC = b cm. If M and N are the midpoints of the nonparallel sides, AD and BC respectively then find the ratio of ar(DCNM) and ar(MNBA).
View SolutionIn figure, DE||BC and the ratio of the areas of △ADEand trapezium BDEC is 4:5 . Find the ratio of DE:BC . If BD = 2cm. Then find AD.
View SolutionIn the given figure, AB and DE are perpendiculars to BC

Find the ratio : area of a DetlaABC: area of ΔDEC.
View SolutionIn the adjoining figure, DE//BC and D divides AB in the ratio 2 : 3. Find :
AEEC
View SolutionIn the adjoining figure, DE//BC and D divides AB in the ratio 2 : 3. Find :
AEAC
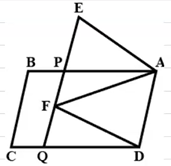
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
View SolutionIn the adjoining figure DE||BC and D divides AB in the ratio 2:3 find.
(i) AEEC (ii) AEAC
View SolutionIn the adjoining figure, DE//BC and D divides AB in the ratio 2 : 3. Find DE, if BC = 7.5 cm.
View Solution

