In given figure, if ∠ACB=∠CDA,AC=8cm and AD=3 cm, then find BD.
To solve the problem step by step, we will use the properties of triangles and the Pythagorean theorem.
Step 1: Understand the Given Information
We are given:
- ∠ACB=∠CDA
- AC=8cm
- AD=3cm
Step 2: Identify Angles
Since ∠CDA=90∘ (as inferred from the context), we can conclude that ∠ACB is also 90∘. This means triangles ACB and CDA are right triangles.
Step 3: Apply the Pythagorean Theorem in Triangle ACB
In triangle ACB:
- AC2=AB2+BC2
- Here, AC=8cm and AD=3cm.
Let AB=3cm and BC=x.
Using the Pythagorean theorem:
82=32+x2
64=9+x2
x2=64−9=55
x=√55
Step 4: Apply the Pythagorean Theorem in Triangle CDA
In triangle CDA:
- Let CD=y and AD=3cm.
Using the Pythagorean theorem:
CD2+AD2=CA2
y2+32=82
y2+9=64
y2=64−9=55
y=√55
Step 5: Relate BD and y
Let BD=y. From the previous calculations, we have found that:
BD=√55
Step 6: Final Calculation
Since we need to find BD:
BD=553
Conclusion
Thus, the length of BD is 553cm.
---
We are given:
- ∠ACB=∠CDA
- AC=8cm
- AD=3cm
Since ∠CDA=90∘ (as inferred from the context), we can conclude that ∠ACB is also 90∘. This means triangles ACB and CDA are right triangles.
In triangle ACB:
- AC2=AB2+BC2
- Here, AC=8cm and AD=3cm.
82=32+x2
64=9+x2
x2=64−9=55
x=√55
In triangle CDA:
- Let CD=y and AD=3cm.
CD2+AD2=CA2
y2+32=82
y2+9=64
y2=64−9=55
y=√55
Let BD=y. From the previous calculations, we have found that:
BD=√55
Since we need to find BD:
BD=553
Thus, the length of BD is 553cm.
Topper's Solved these Questions
- TRIANGLESBook:NCERT EXEMPLAR ENGLISHChapter:TRIANGLESExercise:Long Answer Type Questions
Explore 18 Videos
- TRIANGLESBook:NCERT EXEMPLAR ENGLISHChapter:TRIANGLESExercise:Very Short Answer Typw Questions
Explore 12 Videos
- SURFACE AREAS AND VOLUMESBook:NCERT EXEMPLAR ENGLISHChapter:SURFACE AREAS AND VOLUMESExercise:LONG ANSWER TYPE QUESTIONS
Explore 20 Videos
Similar Questions
In the given figure, if DE || BC, AE = 8 cm, EC = 2 cm and BC = 6 cm, then find DE
View SolutionIn the given figure, if AC=3cm and CB=6cm, find the length of CR.
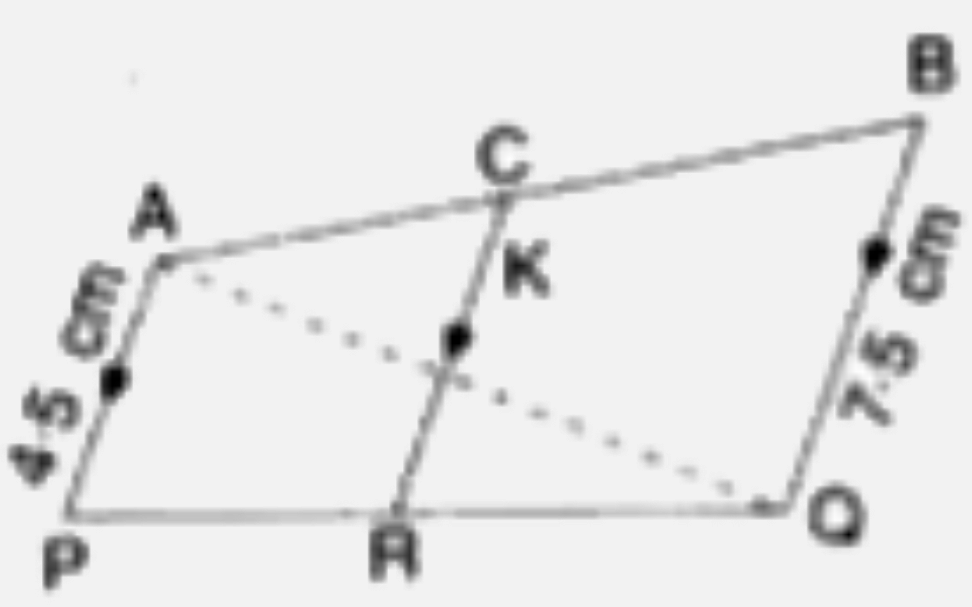
View SolutionIn theadjoining figure, ∠DAB=∠ABC and AD=BC prove that BD=AC.
View SolutionIn the given figure △ACB~△APQ. If BC= 8cm , PQ = 4cm BA= 6.5 cm, AP = 2.8 cm, find CA and AQ.
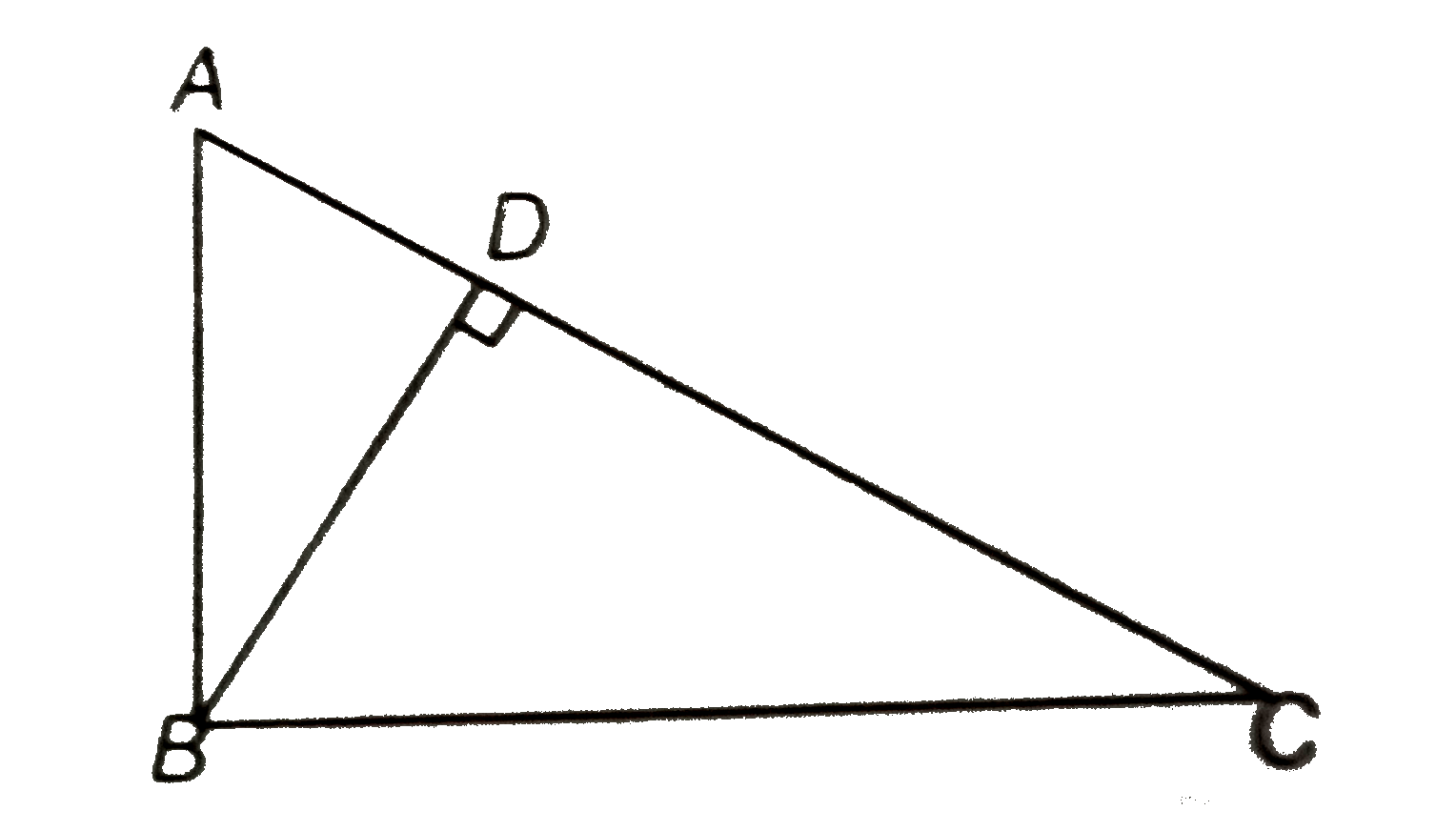
View SolutionIn given figure, ABC is a triangle right angled at B and BD⊥AC. If AD=4 cm and CD= 5 cm, then find BD and AB.
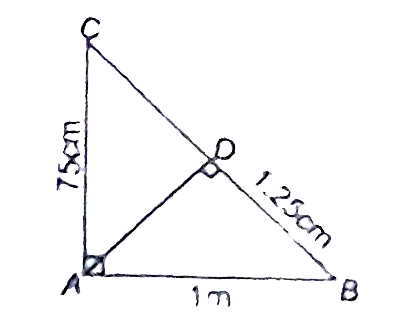
View Solutionin the given figure ∠CAB=90∘andAD⊥BC. if AC= 75 cm , AB= 1m and BD= 1.25 m . Find AD.
View SolutionIn the given figure, AB, BC and CA are tangents to the given circle. If AB= 12cm, BC= 8cm and AC= 10cm, find the length of AD,BE=CF
View SolutionIn the given figure, AB∣∣CD,AB=7cm,BD=25cmandCD=17cm, find the length of side BC.

View SolutionIn the given figure,
AB=AC,∠A=∠D=90∘
BD = 18 cm and DC =24 cm .
Calculate the length of AB correct to two places of decimal. Also . Find the perimeter of quadrilateral ABDC.
View SolutionIn the given figure, BC=8cmandAD=4cm.AD∣∣BC, find the area of ΔEBC

View Solution

