If P + Q = R and P - Q = S, prove that R2+S2=2(P2+Q2)
Video Solution
Text Solution
R2=P2Q2+2PQcosθ…..(i)
S2=P2+Q2−2PQcosθ(i)
Adding these two equations we get,
R2+S2=2(P2+Q2)
|
Topper's Solved these Questions
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Example
40 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - check point 2.1
15 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Single Correct
39 Videos
- UNITS, DIMENSIONS & ERROR ANALYSIS BOOK - DC PANDEY ENGLISHCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Medical entrances gallery
32 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
Similar Questions
if p:q::r, prove that p:r=p2:q2.
View SolutionIn PQR, QM⊥PR and PR2−PQ2=QR2 . Prove that QM2=PM×MR
View SolutionIn PQR, QM⊥PR and PR2−PQ2=QR2 . Prove that QM2=PM×MR
View SolutionIn PQR, QM⊥PR and PR2−PQ2=QR2 . Prove that QM2=PM×MR
View SolutionIn Figure, If PQ=PT and ∠TPS=∠QPR, prove that PRS is isosceles
View SolutionIn Figure, PS=QR and ∠SPQ=∠RQP. Prove that PQS ≅ QPR, PR=QS and ∠QPR= ∠PQS
View SolutionIn Fig 7.51, PR > PQand PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.

View SolutionIn Figure, ∠PQR= ∠PRQ, then prove that ∠PQS= ∠PRT.
View SolutionIn Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.
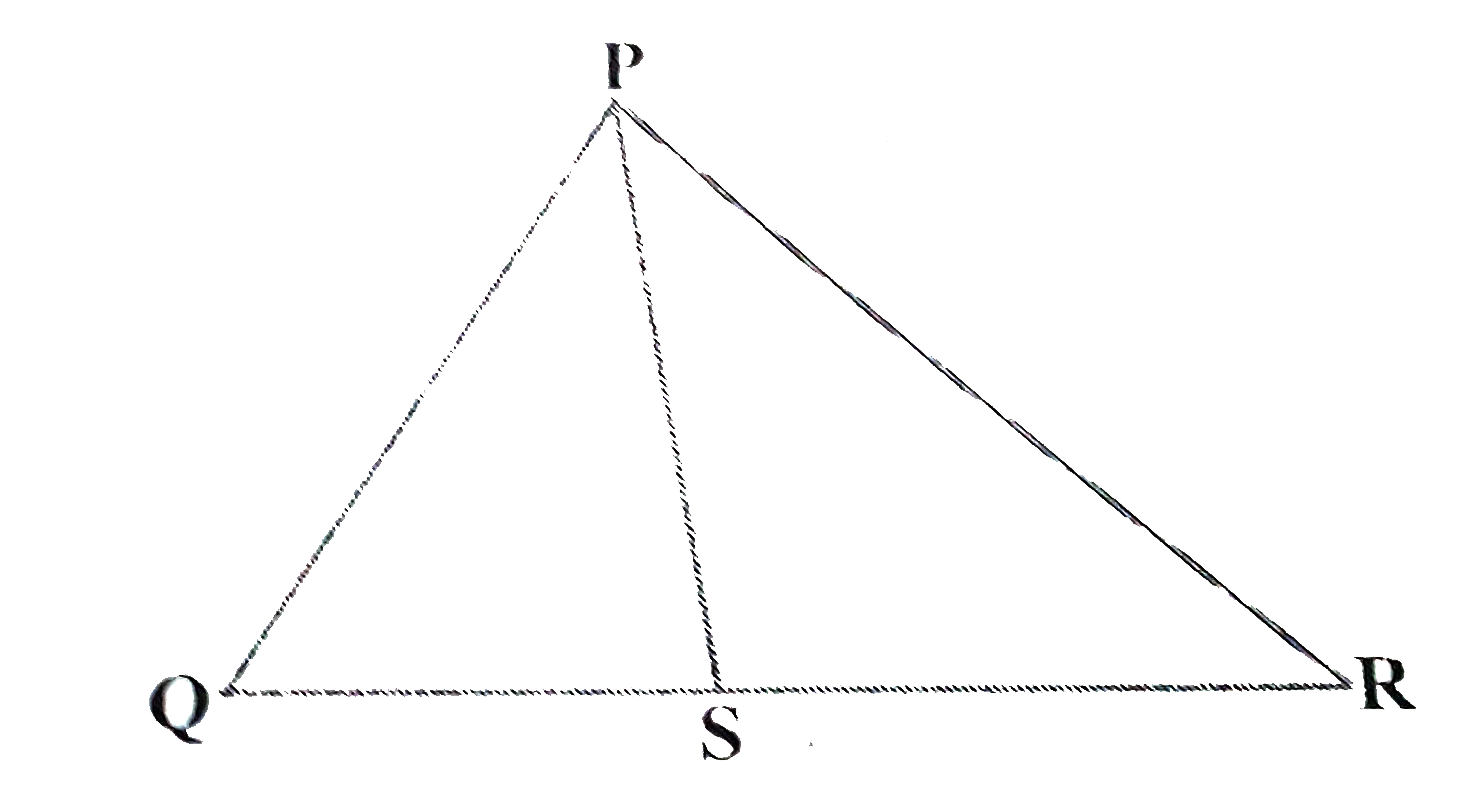
View SolutionIn figure PS is the bisector of ∠QPRof ΔPQR. Prove that QSSR=PQPR.
View Solution
