Question

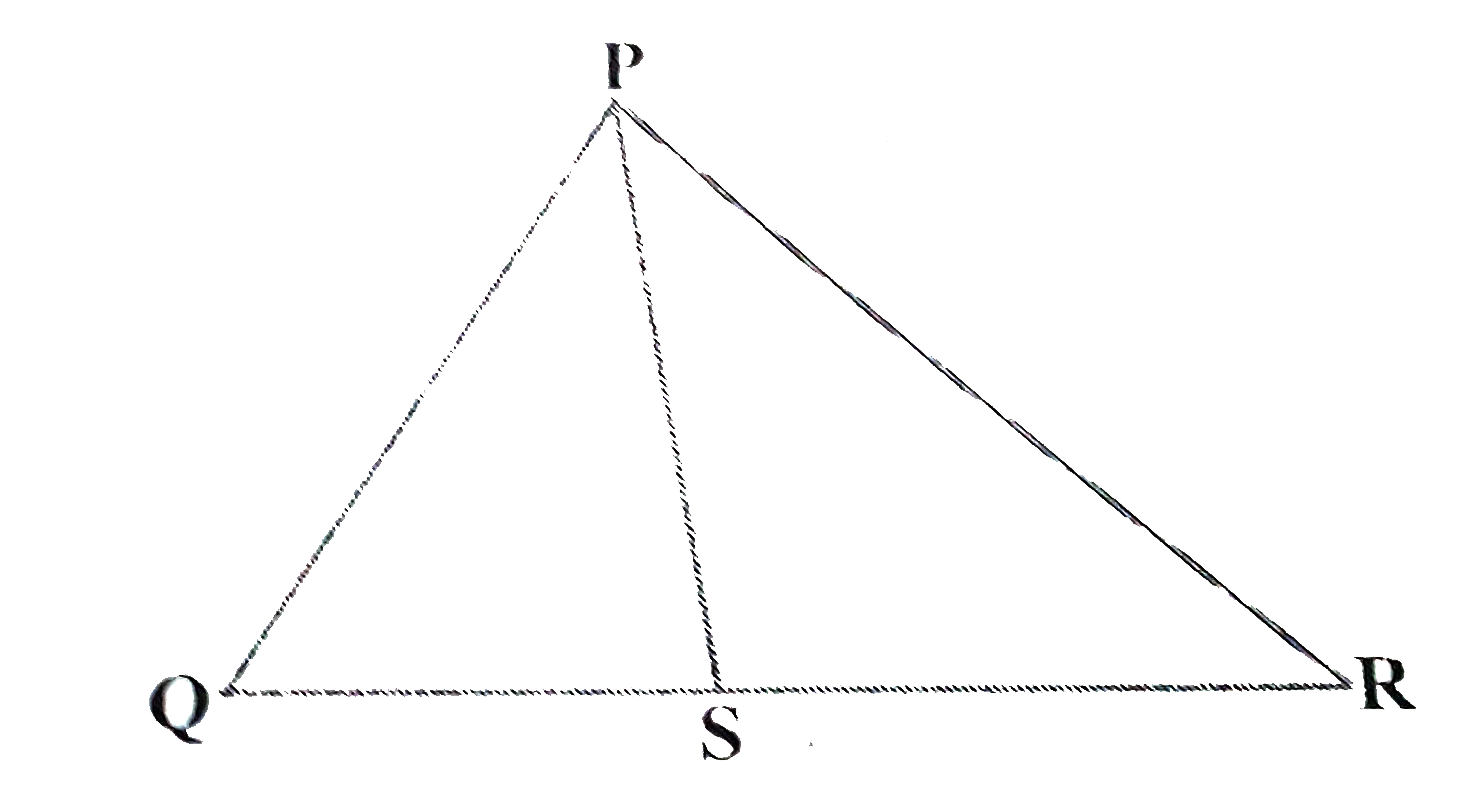
In $PQR,QM\perp PR$
and $P{R}^2-P{Q}^2=Q{R}^2$
. Prove
that $Q{M}^2=PM\times MR$

Explanation

To solve the problem, we need to prove that $$Q{M}^2=PM\times MR$$ given that in triangle $$PQR$$, $$QM\perp PR$$ and $$P{R}^2-P{Q}^2=Q{R}^2$$.

1. Understanding the Given Information:
- We have triangle \( PQR \) with \( QM \) perpendicular to \( PR \).
- The equation \( PR^2 - PQ^2 = QR^2 \) suggests that we can apply the Pythagorean theorem.

2. Identifying the Right Angle:
- From the equation \( PR^2 - PQ^2 = QR^2 \), we can rearrange it to \( PR^2 = QR^2 + PQ^2 \).
- This indicates that \( PR \) is the hypotenuse of triangle \( PQR \), and thus \( \angle Q \) is \( 90^\circ \).

3. Drawing the Diagram:
- Draw triangle \( PQR \) with points \( P \), \( Q \), and \( R \).
- Mark point \( M \) on line \( PR \) such that \( QM \perp PR \).

4. Labeling Angles:
- Let \( \angle P = 1 \) and \( \angle R = 2 \).
- Since \( \angle Q = 90^\circ \), we have \( 1 + 2 + 90^\circ = 180^\circ \).

5. Using Triangle Properties:
- In triangle \( PQM \), we have angles \( 1 \), \( 90^\circ \), and \( \angle PMQ \).
- In triangle \( QMR \), we have angles \( 2 \), \( 90^\circ \), and \( \angle QMR \).

6. Establishing Angle Relationships:
- From the triangles, we can conclude:
- \( \angle PMQ = 2 \) (since \( \angle PMQ + 1 + 90^\circ = 180^\circ \))
- \( \angle QMR = 1 \) (since \( \angle QMR + 2 + 90^\circ = 180^\circ \))

7. Proving Similarity of Triangles:
- Since \( \angle PMQ = \angle QMR \) and both triangles share the right angle, triangles \( PQM \) and \( QMR \) are similar by AA (Angle-Angle) similarity.

8. Setting Up Proportions:
- From the similarity of triangles, we have:
\( \frac{PQ}{QR} = \frac{QM}{MR} = \frac{PM}{QM} \)

9. Cross-Multiplying:
- From the proportion \( \frac{QM}{MR} = \frac{PQ}{QR} \), we can write:
\( QM \cdot QR = PQ \cdot MR \)
- Rearranging gives:
\( QM^2 = PM \cdot MR \)

10. Conclusion:
- We have proved that \( QM^2 = PM \times MR \), which is what we needed to show.