Let →Aand→B be the two vectors of magnitude 10 unit each. If they are inclined to the X-axis at angles 30∘and60∘ respectively, find the resultant.
The correct Answer is:A, B, C, D
R=[(10cos30∘)ˆi+(10cos60∘)ˆj]
+[(10cos60∘)ˆi+(10cos30∘)ˆj]
=10(cos30∘+cos60∘)ˆi+10(cos60∘+cos30∘)ˆj
=10(2cos45∘cos15∘)ˆi+10(cos45∘cos15∘ˆj
=Rxˆi+Ryˆj
Here, Rx=Ry=10√2cos15∘
∴|R|=√R2x+R2y=20cos15∘
since Rx=Ry, therefore,θ=45∘ .
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Example40videos
VECTORS
- BOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - check point 2.115videos
VECTORS
- BOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Single Correct39videos
VECTORS
- BOOK - DC PANDEY ENGLISHCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Medical entrances gallery32videos
UNITS, DIMENSIONS & ERROR ANALYSIS
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question11videos
WAVE MOTION
Similar Questions
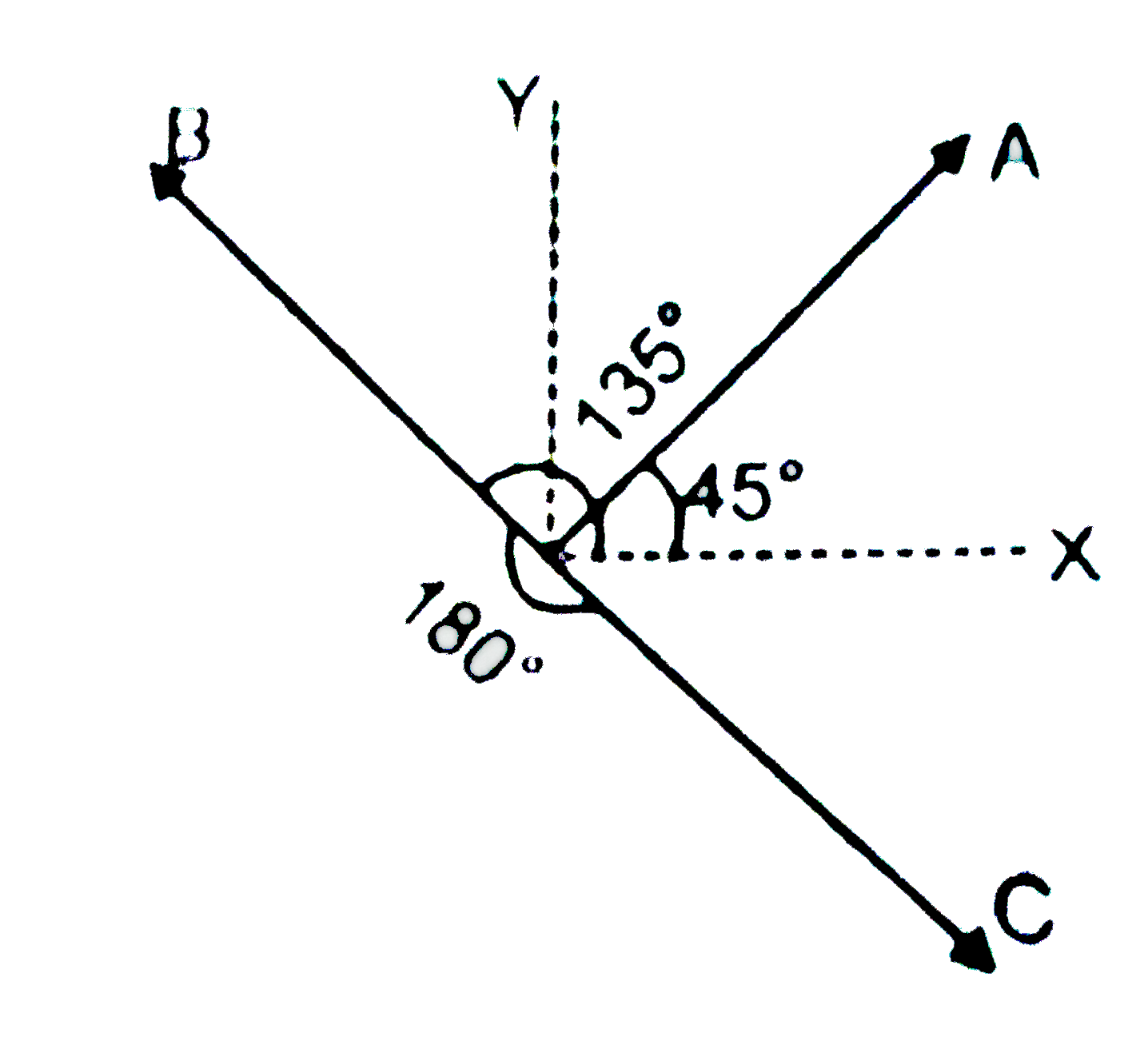
Add vectors →A,→Band→C each having magnitude of 100 unit and inclined to the X-axis at angles 45∘,135∘and315∘ respectively.
View SolutionIf →aand→b are unit vectors inclined to x-axis at angle 30∘and120∘ then ∣∣→a+→b∣∣ equals
View SolutionIf →aand→b are two vectors of magnitude 1 inclined at 120∘, then find the angle between →band→b−→a.
View SolutionAdd vectors →A,→B and →C which have equal magnitude s of 50 unit and are inclined at angles of 45∘,135∘ and 315∘ respectively from x-axos.
 View Solution
View SolutionAdd vectors →A,→B and →C which have equal magnitude s of 50 unit and are inclined at angles of 45∘,135∘ and 315∘ respectively from x-axos.
 View Solution
View SolutionLet →a and →b be two vectors of the same magnitude such that the angle between them is 60∘ and →a.→b=8. Find |→a| and ∣∣→b∣∣.
View SolutionA vector →A makes an angle of 20∘and→B makes an angle of −−→110∘ with the X-axis. The magnitude of these vectors are 3 m and 4 m respectively.Find the resultant
View SolutionTwo vectors having magnitude 12 and 13 are inclined at and angle45∘ to each other.find their resultant vector.
View SolutionLet →a and →b are unit vectors inclined at an angle α to each other , if ∣∣→a+→b∣∣<1 then
View SolutionLet →aand→b be two unit vectors and α be the angle between them, then →a+→b is a unit vector , if α =
View Solution
