In the adjoining figure, common tangents AB and CD to two circles intersect at P.
Prove that AB=CD.
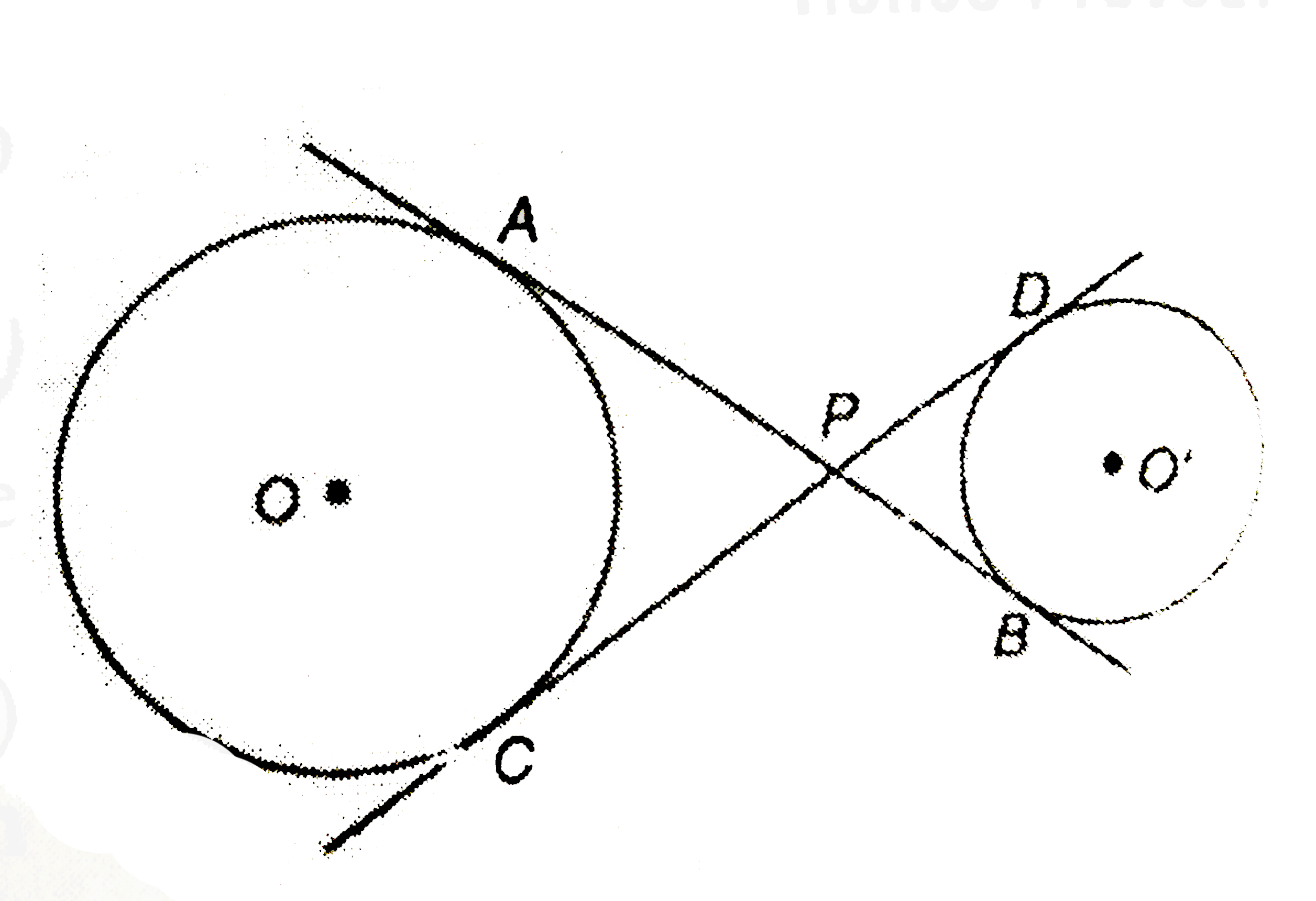
Since PA and PC are two tangents to a circle with centre O from an external point P.
∴ PA=PC …(1)
Also, since PB and PD are two tengents to a circle with centre O' from an external point P.
Circles
∴ PB=PD
Adding (2) and (1), we get
PA+PB=PC+PD
⇒ AB=CD (∵ AB and CD are two straight lines) Hence Proved.
Topper's Solved these Questions
- CIRCLESBook:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLESExercise:Problems From NCERT/exemplar
Explore 11 Videos
- CIRCLESBook:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLESExercise:Exercise
Explore 32 Videos
- ARITHMETIC PROGRESSIONBook:NAGEEN PRAKASHAN ENGLISHChapter:ARITHMETIC PROGRESSIONExercise:Revision Exercise Long Answer Question
Explore 5 Videos
- CO-ORDINATE GEOMETRYBook:NAGEEN PRAKASHAN ENGLISHChapter:CO-ORDINATE GEOMETRYExercise:Revision Exercise Short Answer Questions
Explore 10 Videos
Similar Questions
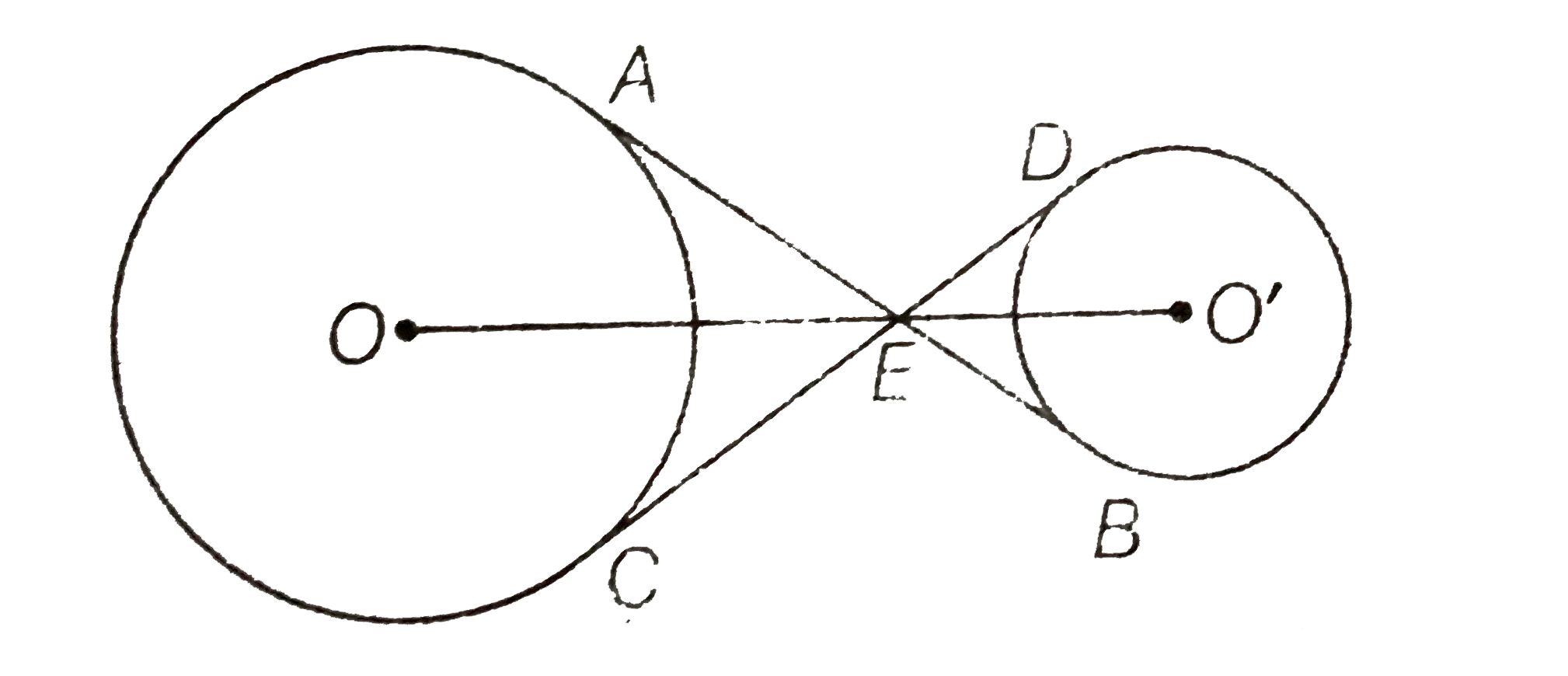
In figure, common tangents AB and CD to two circles intersect at E. Prove that AB=CD.

View SolutionIn Figure, common tangents P Q and RS to two circle intersect at A. Prove that PQ=RS
View SolutionIn a figure the common tangents, AB and CD to two circles with centers O and O' intersect at E. Prove that the points O, E and O' are collinear.
View SolutionIn figure, AB and CD are common tangents to two circles of equal radii. Prove that AB=CD.

View SolutionIn figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB=CD

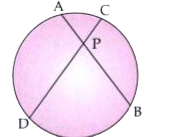
View SolutionAB and CD are two chords of a circle intersecting at P. Prove that AP×PB=CP×PD
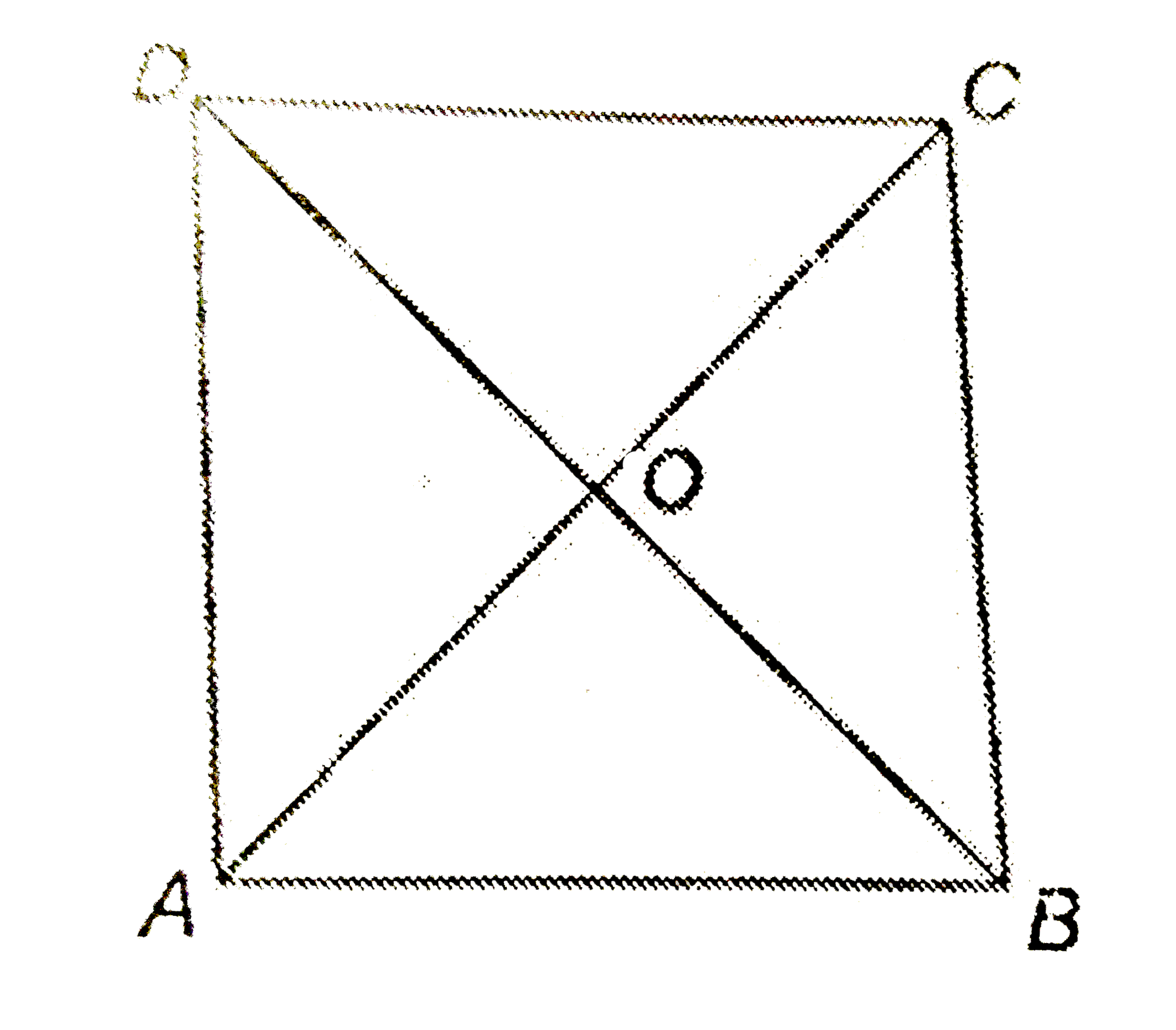
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect point O. Prove that :
AB+BC+CD+DA<2(AC+BD)
View SolutionIn the adjoining figure. If two equal chords AB and CD of a circle intersect each other at E. then prove that chords AC and DB are equal.
View SolutionIn the adjoining figure AB||CD, find x and y

View SolutionIn the adjoining figure, if chords AB and CD of the circle intesect each other at right angles, then find the value of x+y.
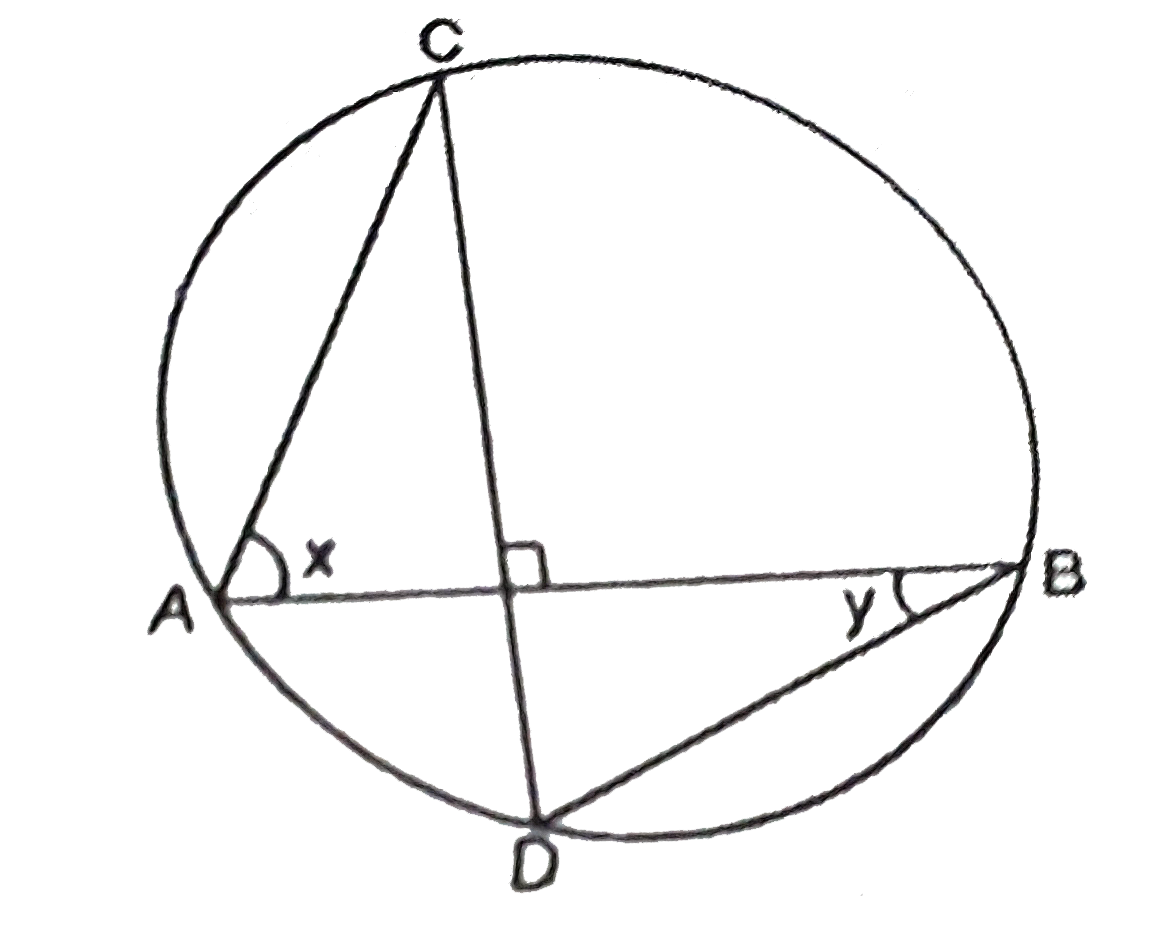
View Solution

