In the adjoining figure, PQRS is a parallelogram. A and B are the mid-points of PQ of SR respectively. If PS= BR, then prove that quadrilateral ADBC is a reactangle.
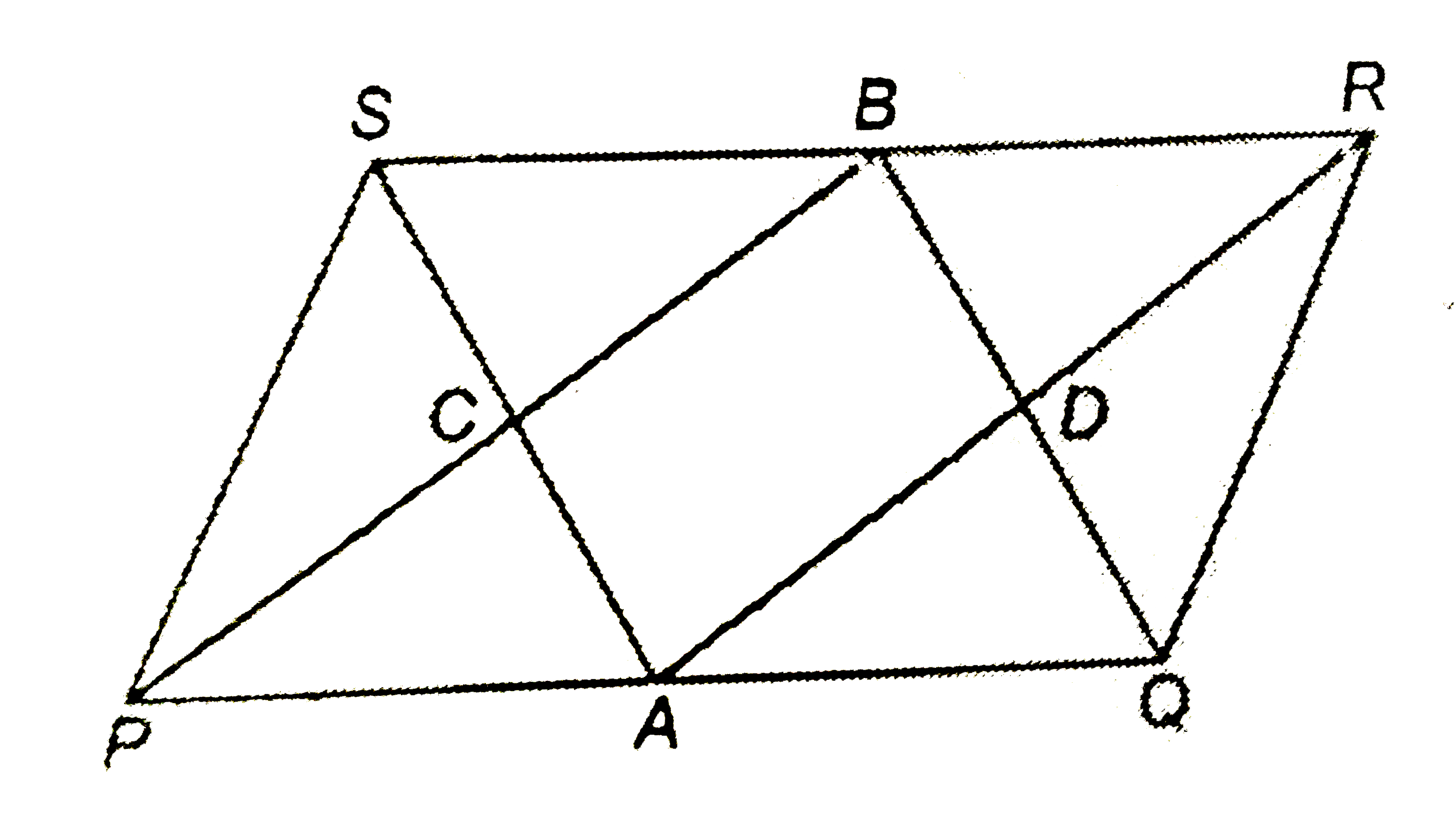
Since □PQRS is a parallelogram
∴ PQ=SRandPS=RQ
⇒ 12PQ=12SR
⇒ PA||SBandAQ=BR ...(1) (∵A and B are mid-points)
AlsoPS=BR=SB=PA ...(2)
Now since PQ||SR
⇒ PA||SB ...(3)
∴ From (1) and (2), we get
□PABS is a parallelogram
But since PA = PS = SB
∴□PABS is a rhombus.
Similarly □AQRB is a rhombus
∴∠1=90∘and∠2=90∘} (∴Diagonals of a rhombus bisceteach other perpendicularly.)
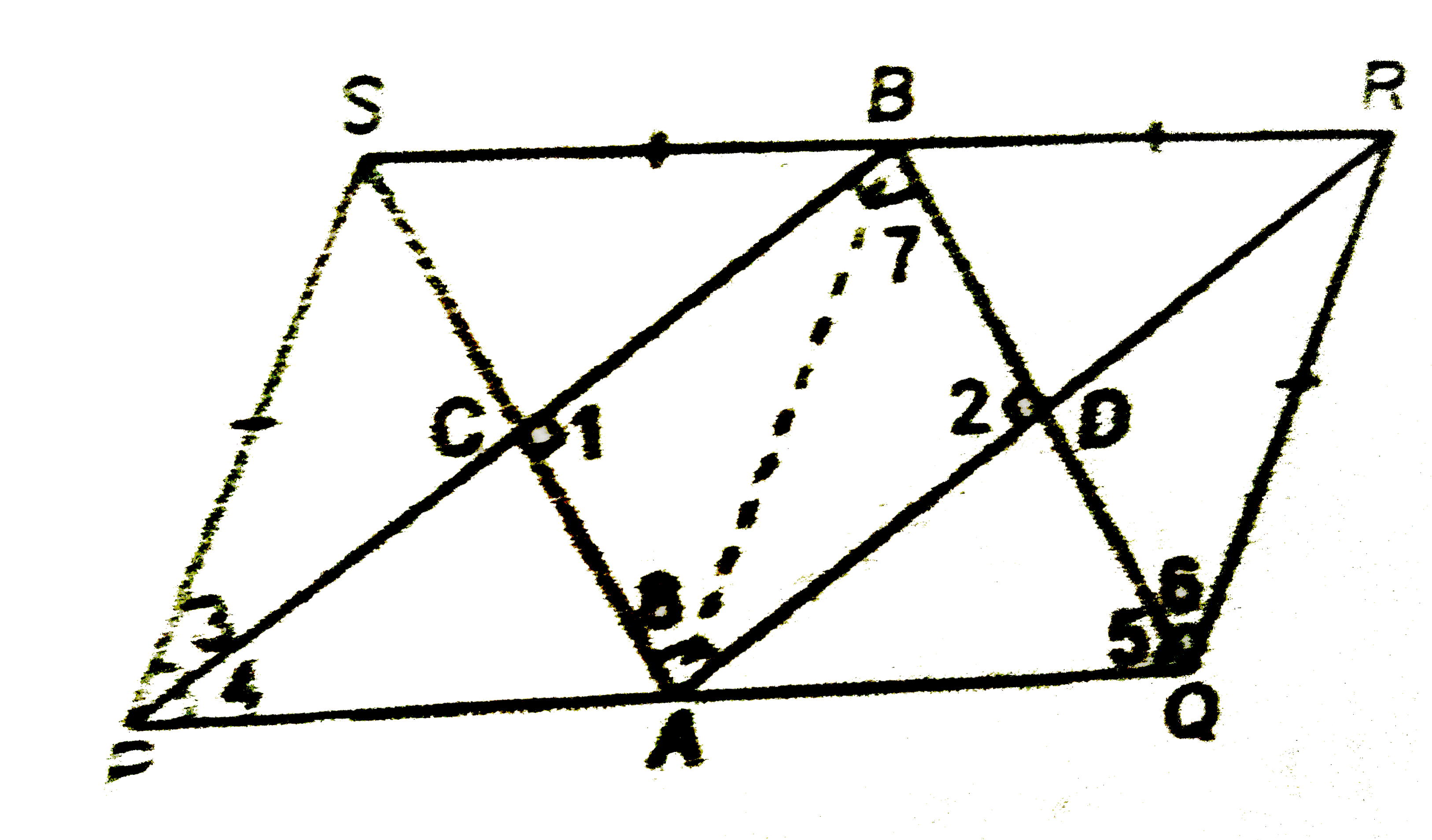
Now, we know that diagongal PB bisects ∠Pand∠Q bisects ∠Q.
(we can prove easily by proving ΔPACandΔPSC coagruent)
But(∠3+∠4+(∠5+∠6=180∘ (sum of oco-interior angles)
⇒ 2∠4+2∠5=180∘
⇒ ∠4+∠5=90∘
⇒ ∠7=90∘
Now, in □ADBC,∠1=∠2=∠7=90∘ (angle sum property)
Each of the 4 angle of a quadrilateral ABCD is 90∘.
So, □ADBC is a reactangle.
Topper's Solved these Questions
- QUADRILATERALSBook:NAGEEN PRAKASHAN ENGLISHChapter:QUADRILATERALSExercise:Problems From NCERT/exemplar
Explore 11 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHAN ENGLISHChapter:QUADRILATERALSExercise:Exercise 8a
Explore 29 Videos
- PROBABILITYBook:NAGEEN PRAKASHAN ENGLISHChapter:PROBABILITYExercise:Revision Exercise (very Short Answer /short Answer Questions)
Explore 10 Videos
- STATISTICSBook:NAGEEN PRAKASHAN ENGLISHChapter:STATISTICSExercise:Revision Exercise
Explore 12 Videos
Similar Questions
In the adjoining figure, prove that ABCD is a parallelogram. Also find its area.
View Solution□PQRS is a reactangle. If A, B and C are the mid-points of PQ, PS and QR respectively, then prove that
AB+AC=12(PR+SQ).
View SolutionPQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR. Show that LM and QS bisect each other.
View SolutionIn the adjoining figure, ABCD and PBCQ are parallelogram. Prove that:

AP= DQ
View SolutionIn the given figures, if PQRS is a parallelogram and AB||PS, then prove that OC||SR.
View SolutionIn the given figure, PQRS is a parallelogram. If X and Y are mid-point of PQ and SR respectively and diagonal SQ is joined. Find the ratio of area of (∣∣gmXQRY): area (ΔQSR)
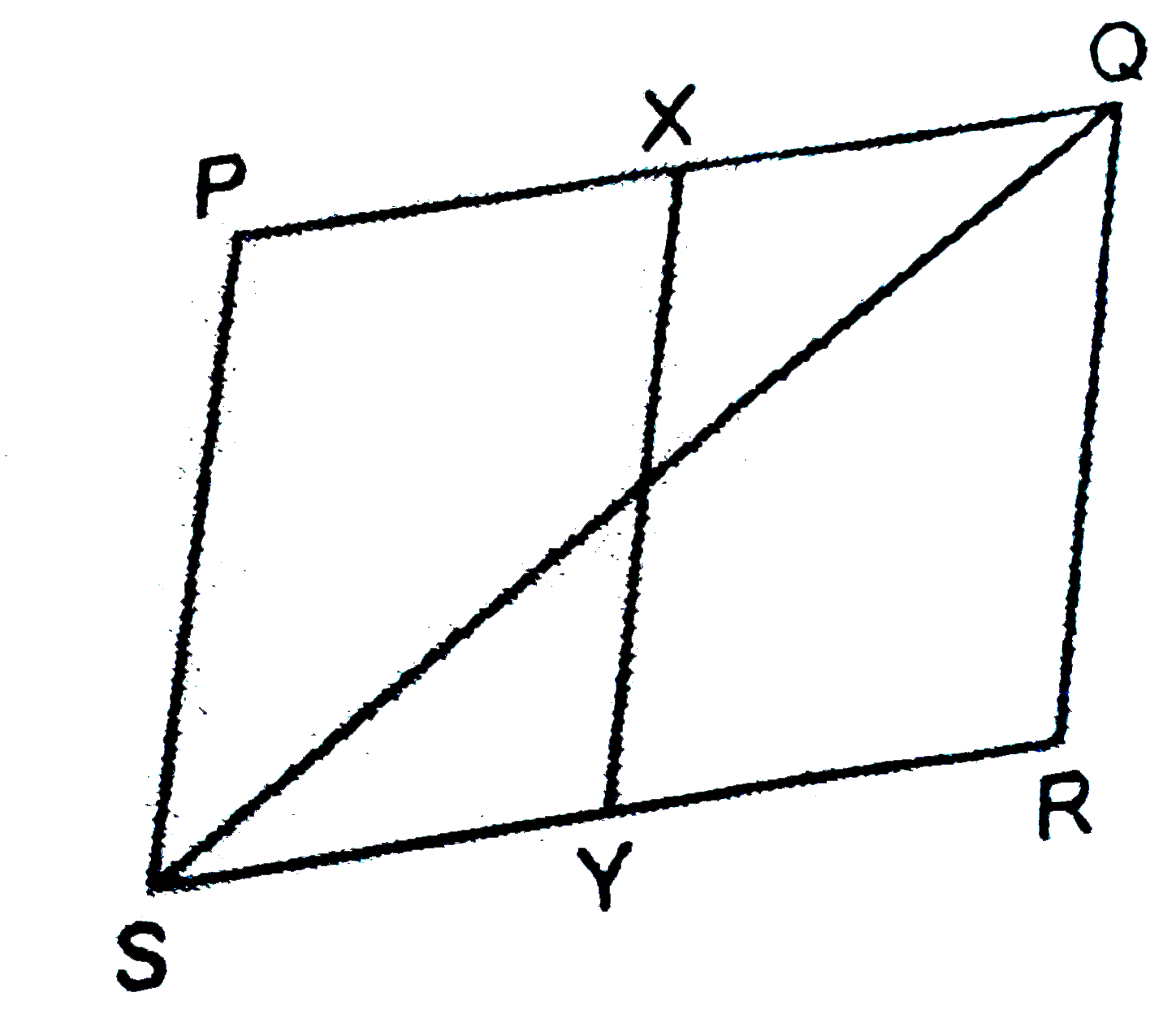
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid-points of sides AB and DC respectively. Show that AXCY is a parallelogram.
View SolutionIn the adjoining figure, ABCD is a parallelogram. If ∠MBC=∠NDA, prove that AM=NC.
View SolutionIf S is the mid-point of side QR of a ΔPQR, then prove that PQ+PR=2PS.
View SolutionIn the adjoining figure, ABCD and PBCQ are parallelogram. Prove that:
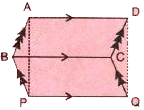
APQD is a parallelogram
View Solution

