In ΔDEFandΔPQR, it is given that ∠D=∠Qand∠R=∠E, then which of the following is not true?
EFPR=DFPQ
DEPQ=EFRP
DEQR=DFPQ
EFRP=DEQR
The correct Answer is:B
To solve the problem, we need to analyze the given information about triangles DEF and PQR.
1. Identify the Given Angles:
We are given that:
- ∠D=∠Q
- ∠R=∠E
2. Apply the Angle-Angle (AA) Similarity Criterion:
Since two angles of triangle DEF are equal to two angles of triangle PQR, we can conclude that:
- Triangle DEF is similar to triangle PQR by the AA similarity criterion.
3. List the Corresponding Angles:
From the similarity, we can state:
- ∠D=∠Q
- ∠E=∠R
- Let’s denote the third angle in triangle DEF as ∠F and the third angle in triangle PQR as ∠P. Therefore, ∠F=∠P (since the sum of angles in a triangle is 180 degrees).
4. Write the Proportionality of Sides:
Since the triangles are similar, the corresponding sides are proportional:
DEQP=EFPR=DFQR
5. Evaluate the Options:
We need to determine which statement is not true based on the proportionality of the sides. The options typically involve ratios of the sides of the triangles.
6. Identify the Incorrect Statement:
Given the proportionality, if an option states something like DEPQ, it would not be true because PQ is not a corresponding side to DE in the similarity relation. The correct corresponding side to DE is QP.
7. Conclusion:
Therefore, the option that states DEPQ is not true, and we can conclude that option B is the incorrect statement.
Final Answer:
The option that is not true is option B.
We are given that:
- ∠D=∠Q
- ∠R=∠E
Since two angles of triangle DEF are equal to two angles of triangle PQR, we can conclude that:
- Triangle DEF is similar to triangle PQR by the AA similarity criterion.
From the similarity, we can state:
- ∠D=∠Q
- ∠E=∠R
- Let’s denote the third angle in triangle DEF as ∠F and the third angle in triangle PQR as ∠P. Therefore, ∠F=∠P (since the sum of angles in a triangle is 180 degrees).
Since the triangles are similar, the corresponding sides are proportional:
DEQP=EFPR=DFQR
We need to determine which statement is not true based on the proportionality of the sides. The options typically involve ratios of the sides of the triangles.
Given the proportionality, if an option states something like DEPQ, it would not be true because PQ is not a corresponding side to DE in the similarity relation. The correct corresponding side to DE is QP.
Therefore, the option that states DEPQ is not true, and we can conclude that option B is the incorrect statement.
The option that is not true is option B.
Topper's Solved these Questions
- TRIANGLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Very Short Answer Typw Questions
12 Videos
- TRIANGLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Short Answer Type Questions
15 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS
20 Videos
Similar Questions
Knowledge Check
If ΔABC~ΔDEF, then which of the following is true?
ABC.EF = AC.FDBAB.ED = AC.DECBC.DE = AB.EFDBC.DE = AB.FD
In a right - angled triangle , it is given that A is an acute angle and tanA=512
sin A
View SolutionIn a right - angled triangle , it is given that A is an acute angle and tanA=512
cos A
View SolutionFind the ara of the given obtuse-angled triangle ABC.

View SolutionWhich of the following pairs of triangles are congruent ? In each case, state the condition of congruency :
(a) In ΔABCandΔDEF, AB = DE, BC = EF and ∠B=∠E.
(b) In ΔABCandΔDEF,∠B=∠E=90∘, AC = DF and BC = EF.
(c) In ΔABCandΔQRP, AB = QR, ∠B=∠Rand∠C=∠P.
(d) In ΔABCandΔPQR, AB = PQ, AC = PR and BC = QR.
(e) In ΔABCandΔPQR, BC = QR, ∠A=90∘,∠C=∠R=40∘and∠Q=50∘.
View SolutionΔPQR is right angled isosceles triangle, right angled at R. Find value of sin P.
View SolutionA median and an altitude of an obtuse-angled triangle lie outside the triangle. It is true ?
View SolutionIn a ΔPQR as show in figure given that x:y:z::2:3:6, then find value of ∠QPR.
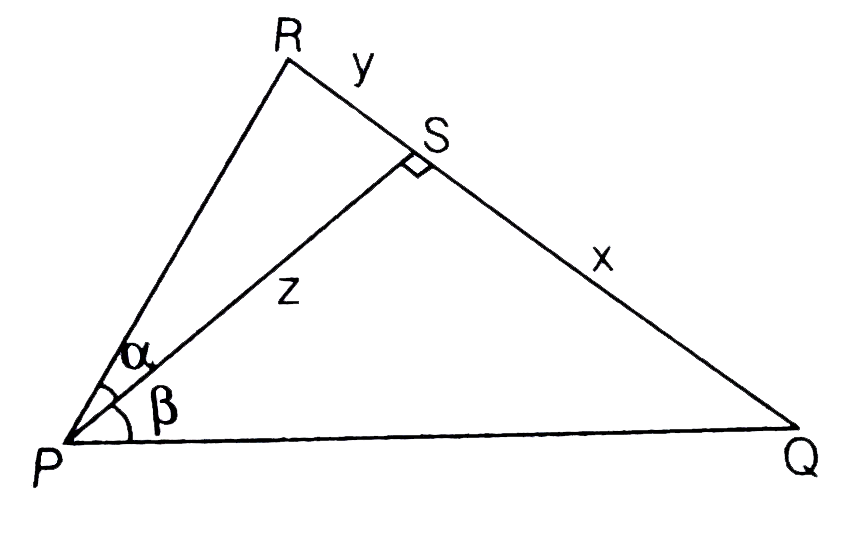
View Solution
