In an isosceles $Δ A B C$ , the base AB is produced both wasys in P and Q such that $A P \times B Q = A C^{2}$
Prove that $Δ A C P ~ Δ B C Q$ .

Video Solution

Text Solution

Verified by Experts

$C A = C B \Rightarrow ∠ C A B = ∠ C B A$
$\Rightarrow 180^{\circ} - ∠ C A B = 180^{\circ} - ∠ C B A$
$\Rightarrow ∠ C A P = ∠ C B Q$ .
Now, $A P \times B Q = A C^{2} \Rightarrow \frac{A P}{A C} = \frac{A C}{B Q}$
$\Rightarrow \frac{A P}{A C} = \frac{B C}{B Q} [∴ A C = B C]$

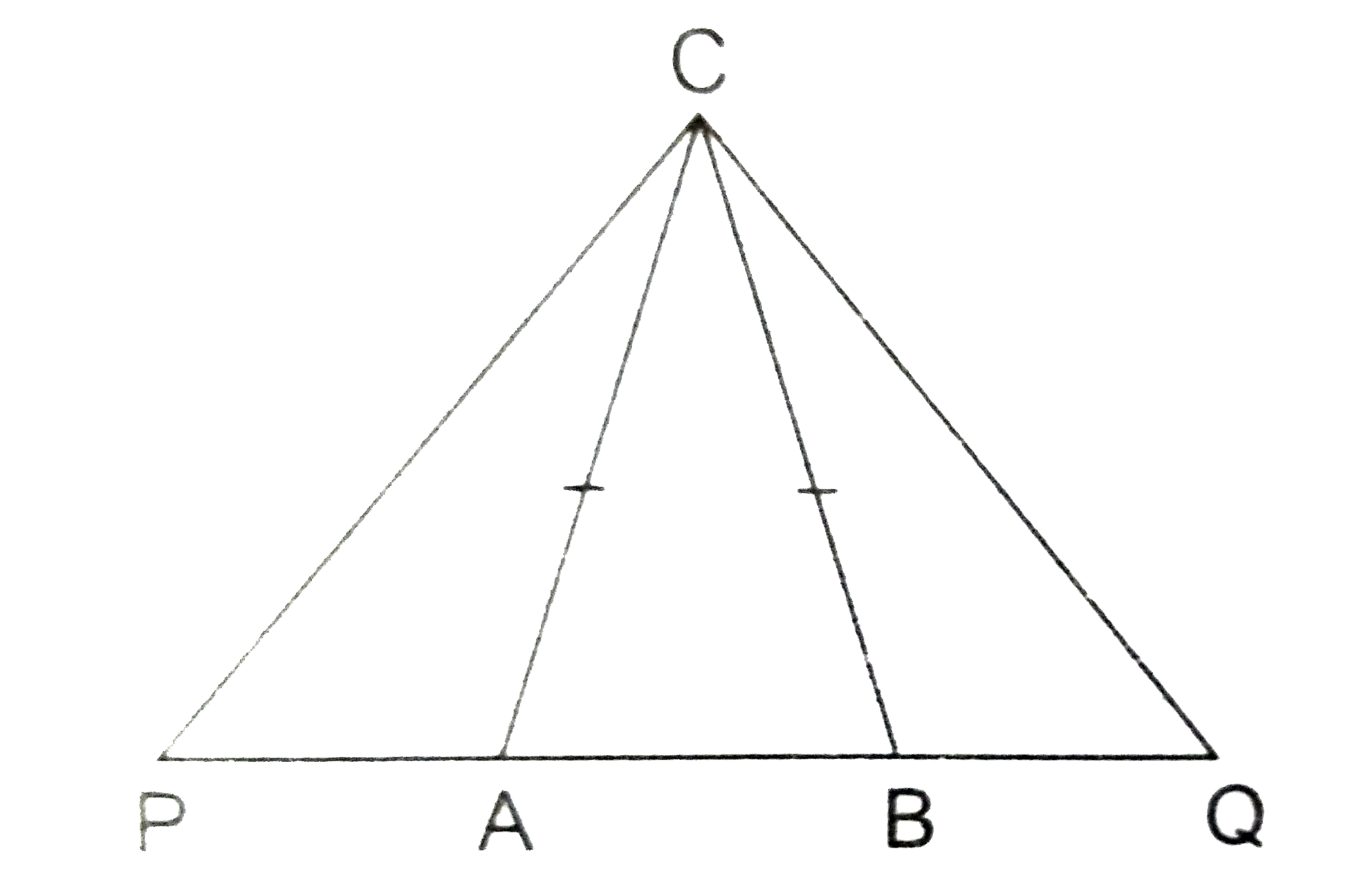
Thus, $∠ C A P = ∠ C B Q and \frac{A P}{A C} = \frac{B C}{B Q}$
$∴ Δ A C P ~ Δ B C Q$ .

Updated on:21/07/2023