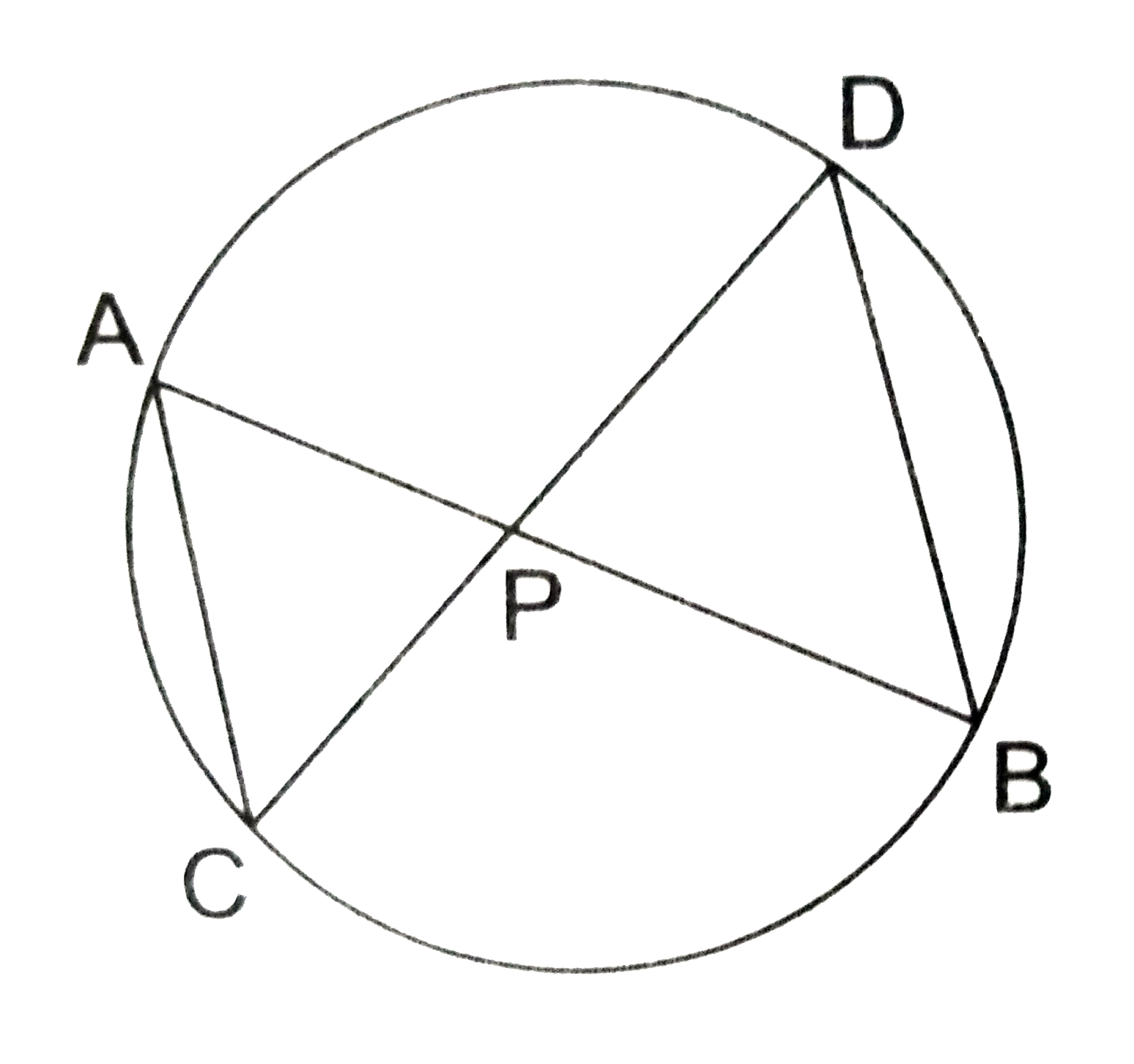
Two chords AB and CD of a circle intersect at a point outside the circle. Prove that
$(a) Δ P A C ~ Δ P D B (b) P A \cdot P B = P C \cdot P D$ .

Video Solution

Text Solution

Verified by Experts

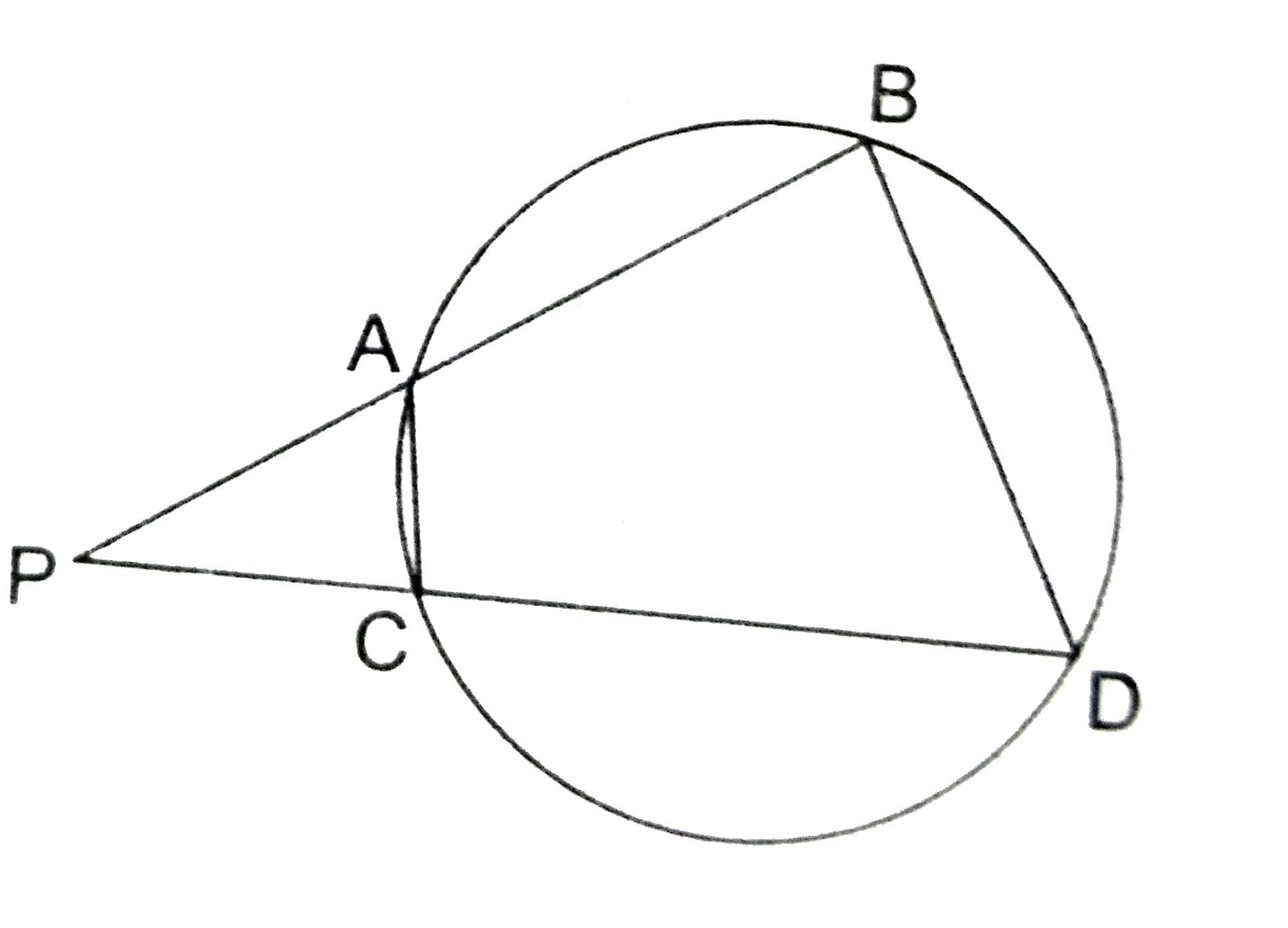
Clearly ABCD is a cyclic quadrilateral.
$∴ ∠ 1 + ∠ 2 = 180^{\circ} ... (i)$
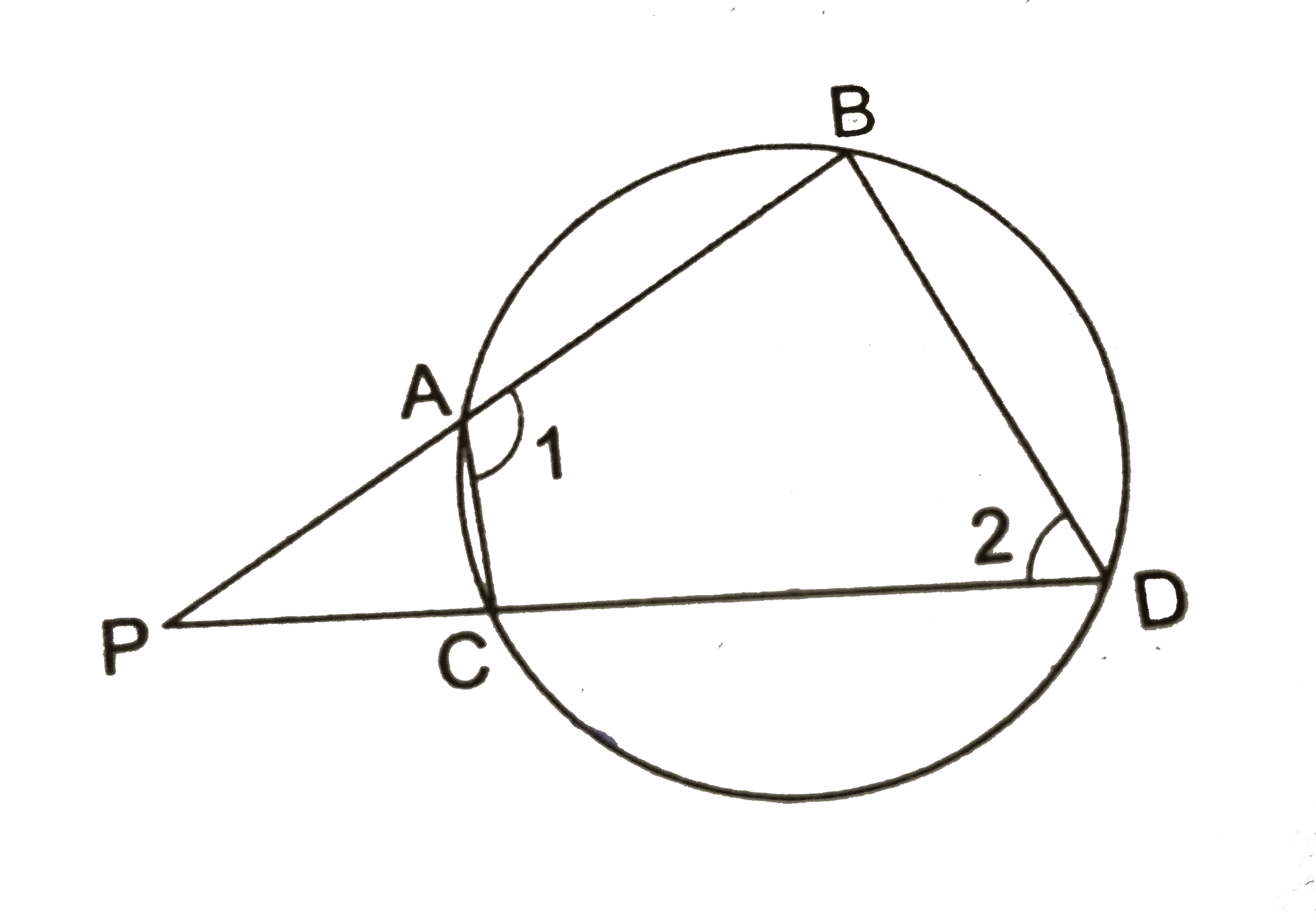
In $Δ P A C and Δ D P B$ , we have
$∠ P A C = ∠ D P B$ [ common]
$∠ P A C = ∠ P D B$ [ each equal to $(180^{\circ} - ∠)$ ]
[ Note $∠ P A C + ∠ 1 = 180^{\circ}$ (linear pair)
and $∠ P D B + ∠ 1 = 180^{\circ}$ [ using]
$∴ Δ P A C ~ Δ P D B$ [ by AA-similarity]
And so, $\frac{P A}{P D} = \frac{P C}{P B} r A r P A \cdot P C \cdot P D$ .

Updated on:21/07/2023

Two chords AB and CD of a circle with centre O intersect at point P within the circle. $∠ A O C + ∠ B O D = ?$
A $∠ A P C$
B $2 ∠ A P C$
C $\frac{3}{2} ∠ A P C$
DNone of these
Two chords AB and CD of a circle are produced to intersect each other at point P outside the circle. If AB=7 cm, BP = 4.2 cm and PD = 2.8 cm, then the length of CD is: /
एक वृत्त की दो जीवाओं AB और CD को बढ़ाया जाता है जो एक-दूसरे को वृत्त के बाहर बिंदु ? पर काटती हैं| यदि AB = 7 सेमी, BP = 4.2 सेमी तथा तथा PD = 2.8 सेमी है, तो CD की लंबाई कितनी है ?
A15.8 cm
B12 cm
C14 cm
D14.6 cm
Chords AB and CD of a circle intersect at a point P inside the circle. If AB = 10 cm, AP = 4 cm and PC = 5 cm, then CD is equal to:
A4.8 cm
B6.8 cm
C9.8 cm
D7.8 cm