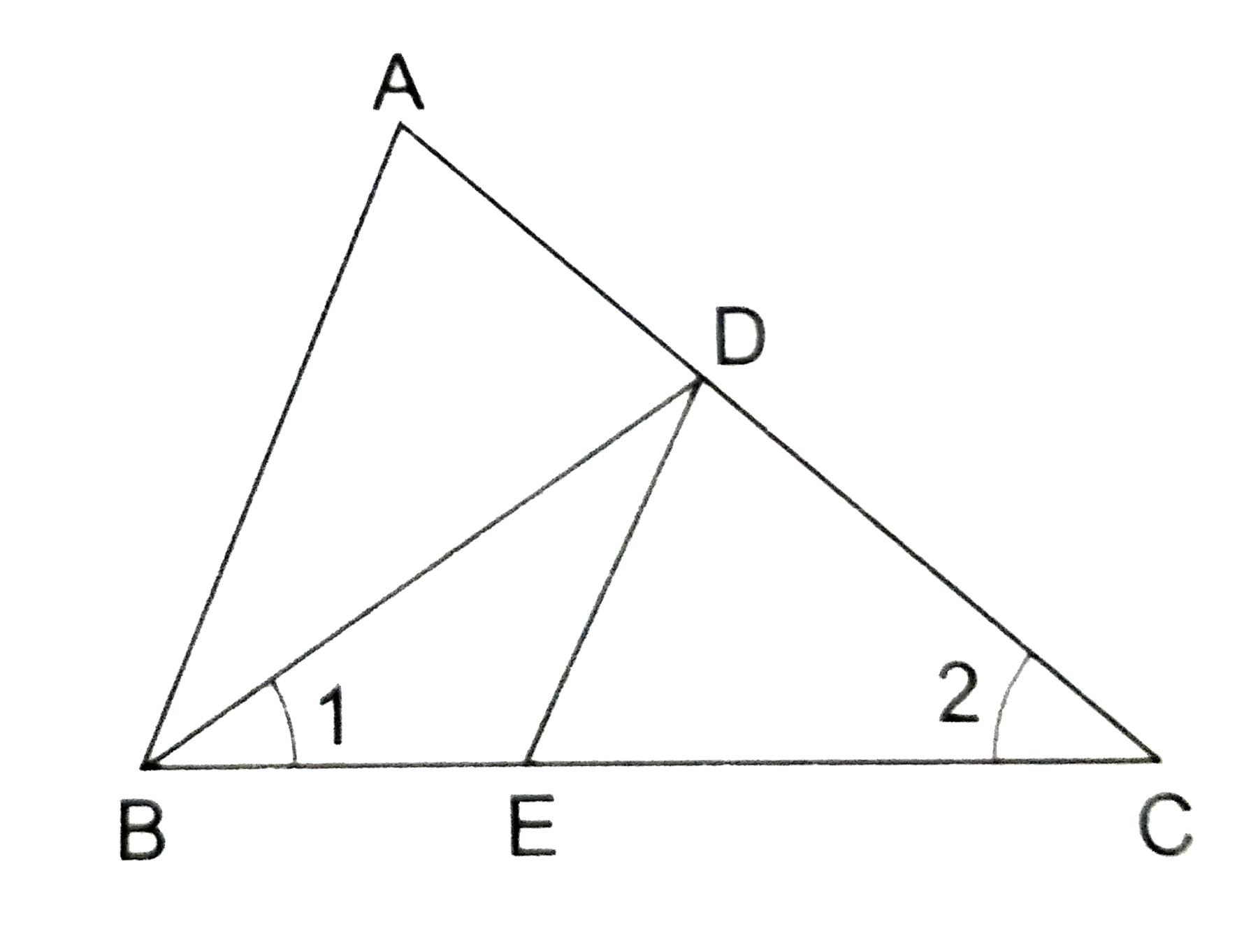
In the given figure, ∠1=∠2andACBD=CBCE prove that ΔACB~ΔDCE.

Video Solution
Text Solution
ACBD=CBCE⇒ACCB=BDCE
Also, ∠2=∠1⇒BD=DC.
Thus, ACCB=DCCE⇒ACDC=CBCE
and ∠ACB=∠DCE=∠C
∴ΔACB~ΔDCE [ SAS- similarity]
|
Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Exercise 7C
Explore 13 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Exercise 7D
Explore 22 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Exercise 7A
Explore 12 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
Knowledge Check
ΔACB≅ΔDFE. Find ∠F
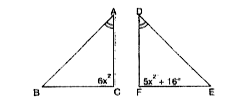 A4∘B96∘C100∘D60∘
A4∘B96∘C100∘D60∘
In the given figure, ∠ACB=90∘andCD⊥AB. Prove that CD2=BD⋅AD

View SolutionIn the adjoining figure, BD = CE and ∠ADB=∠AEC=90∘, prove that
(i) ΔABD≅ΔACE (ii) ABC is an isosceles triangle.

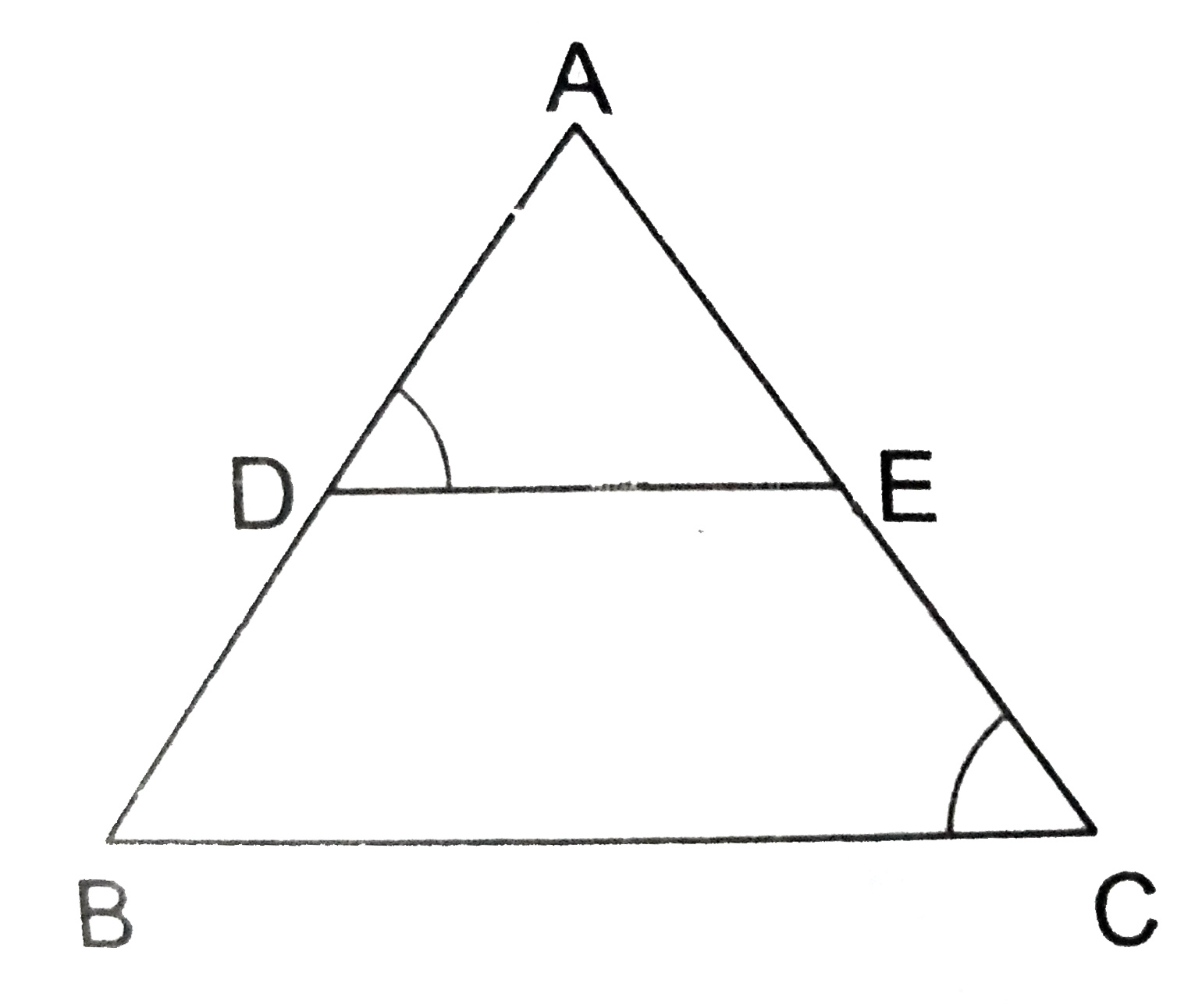
View SolutionIn the given figure, ADDB=AEEC and ∠ADE=∠ACB. Prove that ΔABC is an isosceles triangle.
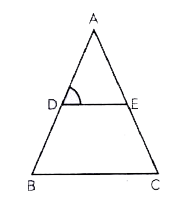
View SolutionIn the given figure, if ∠D=∠C, then it is true that △ADE~△ACB? Why?
View SolutionIn the given figure , AB=CD,CE=BF and ∠ACE==∠DBF . Prove that
AE=DF
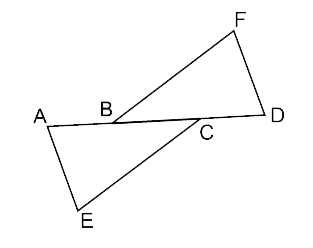
View SolutionIn the given figure, AB = AC and AD = AE. Prove that:
BD = CE
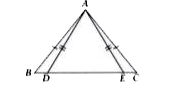
View SolutionIn the given figure , if AB = BC , ∠BAD=∠CAE then prove that △ADE is an isosceles triangle .

View Solution

