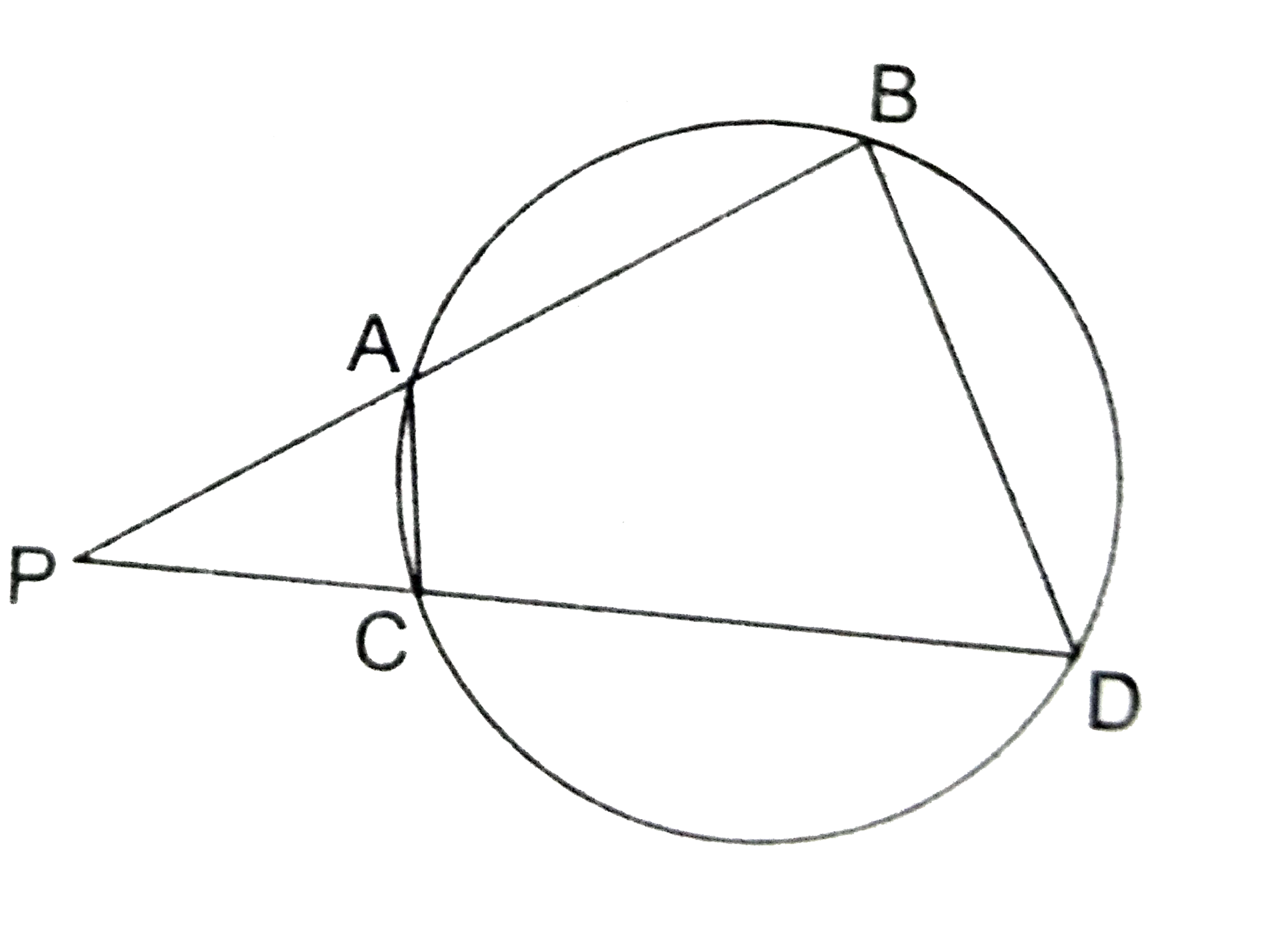
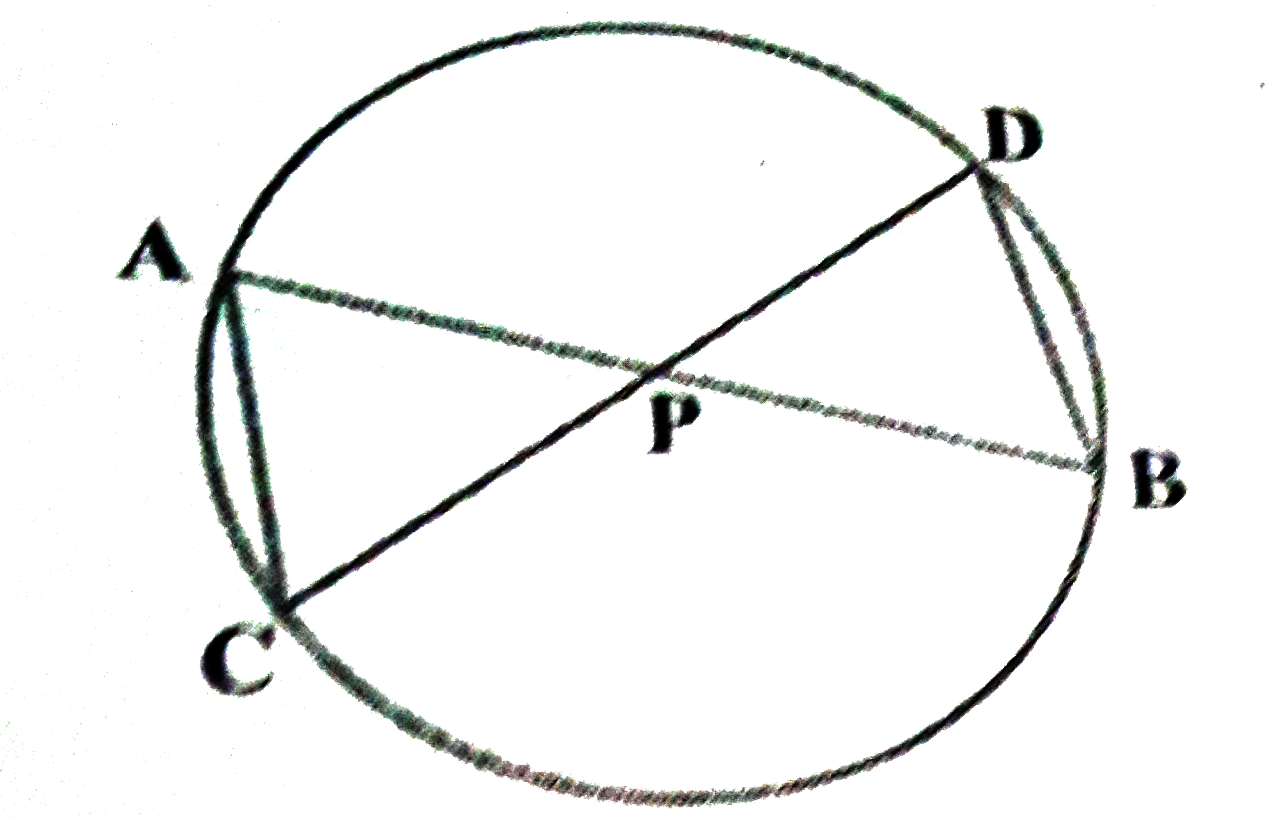In a cricle, two chords AB and CD intersect at a point P inside the circle. Prove that
(a)ΔPAC~ΔPDB (b)PA⋅PB=PC⋅PD.
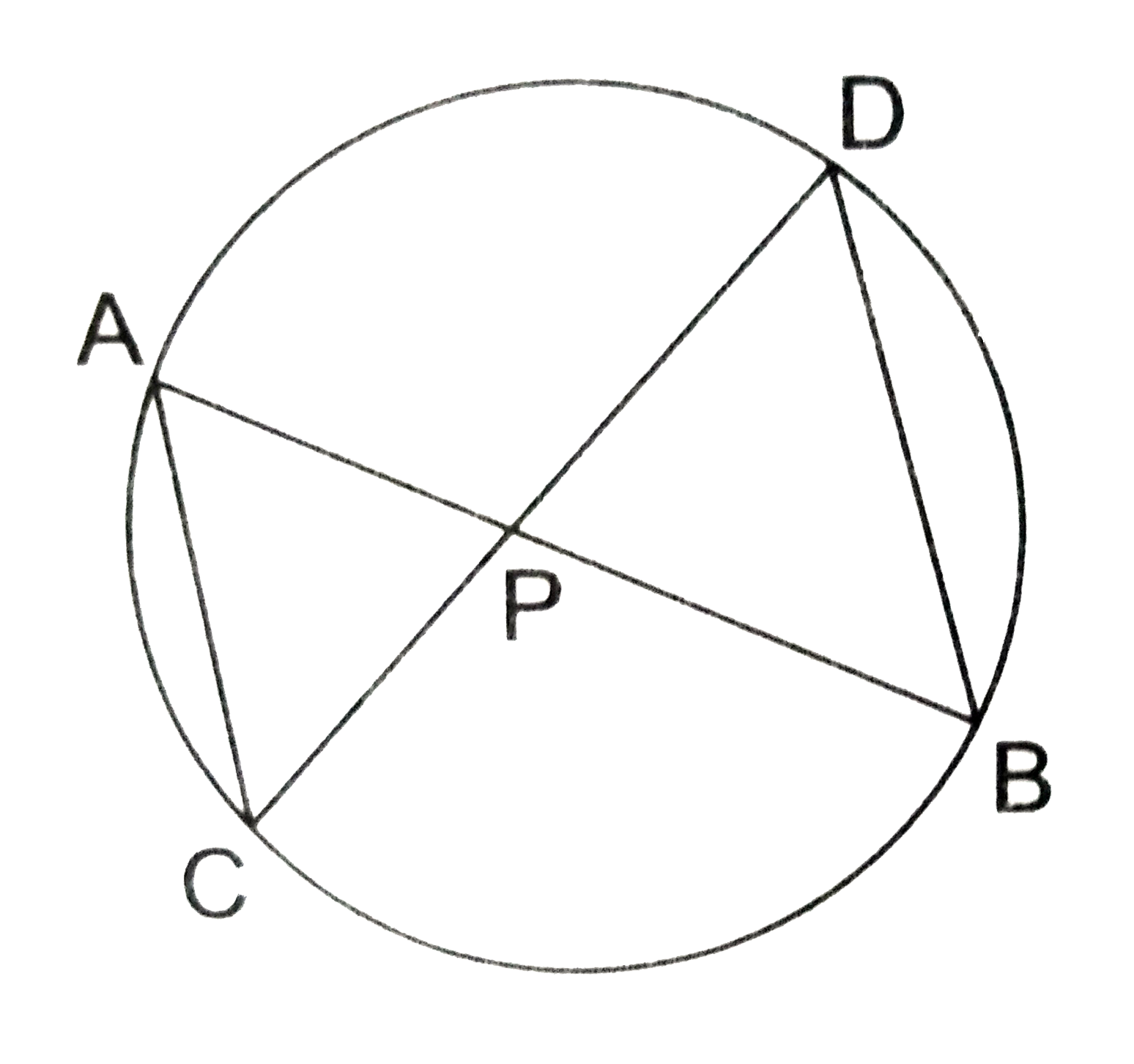
In ΔPACandΔPDB, we have
∠APC=∠DPB [ vertically oppsite angles]
∠PAC=∠PDB [ angles in the same segment]
∴ΔPAC~ΔPDB [ by AA-similarity]
And so, PAPD=PCPB⇒PA⋅PB=PC⋅PD.
Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Exercise 7C
Explore 13 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Exercise 7D
Explore 22 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Exercise 7A
Explore 12 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
Knowledge Check
Vinod have 20 rupees. He bought 1, 2, 5 rupee stamps. They are different in numbers by the reason of no change, the shop keeper gives 3 one rupee stamps. So how many stamps Vinod have ?
AA) 10BB) 18CC) 12DD) 15Two mutually perpendicular chords AB and CD intersect at point P inside the circle such that CP=15cm.,PD=8cmandPB=6cm. Find the length AC (in cm.)
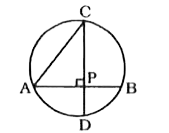 A25B24C20D18
A25B24C20D18
In the figure, two chords AB and CD intersect each other at the point P.
Prove that : ΔAPC~ΔDPB
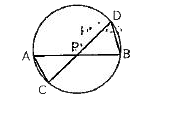
View SolutionIn the figure, two chords AB and CD intersect each other at the point P.
Prove that : AP. PB = CP. DP
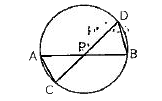
View SolutionIn a circle, chords AB and CD intersect at a point R inside the circle. If AR : RB = 1:4 and CR: RD = 4:9, then the ratio AB: CD is
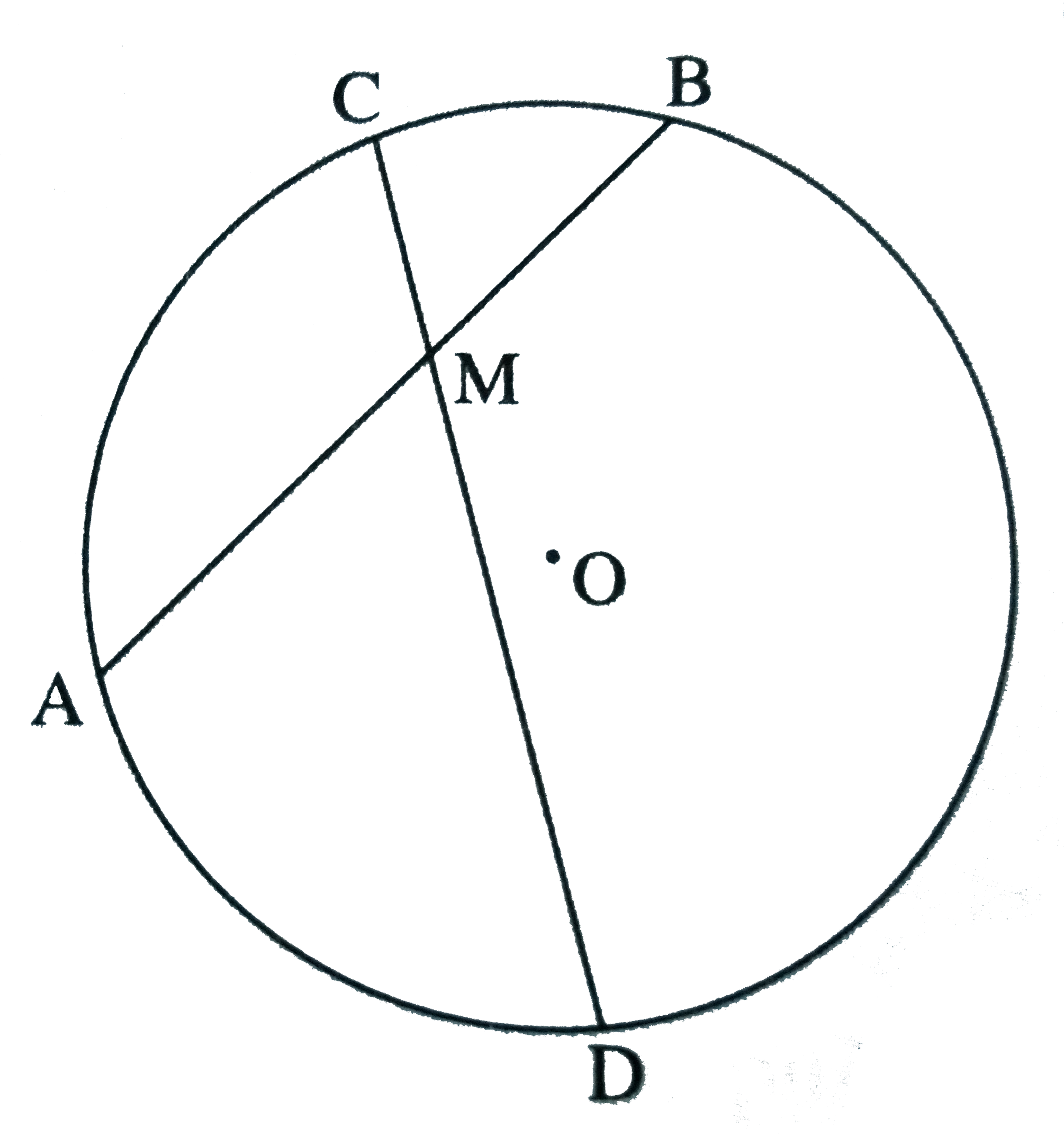
View SolutionIn the figure, chord AB and chord CD intersect at point M inside the circle such that AM=4, BM=3, CM=2, then CD=………
View SolutionIn a circle with centre O, chords ABandCD intersect inside the circumference at E. Prove that ∠AOC+∠BOD=2∠AEC.
View SolutionIn a circle with centre O, chords AB and CD intersect inside the circumference at E. Prove that ∠AOC+ ∠BOD=2 ∠AEC
View Solution