In a circle with centre O, chords AB and CD intersect inside the circumference at E. Prove that ∠AOC+ ∠BOD=2 ∠AEC
Consider AC of the circle with center at O.
Now, arc AC subtends ∠AOC at the center and ∠ABC at the remaining part of the circle.
So, ∠AOC=2∠ABC____1
Similarly, arc BD subtends ∠BOD at the center and ∠BCD at the remaining part of the circle.
∴ ∠BOD=2∠BCD___2
Adding 1 and 2
∠AOC+∠BOD=2(∠ABC+∠BCD)
∠AOC+∠BOD=2∠AEC
Since ∠AEC is the exterior angle and ∠ABC and ∠BCD are interior angles of △BEC)
Hence, (∠ABC+∠BCD=2∠AEC).
Topper's Solved these Questions
Similar Questions
In a circle with centre O, chords ABandCD intersect inside the circumference at E. Prove that ∠AOC+∠BOD=2∠AEC.
View SolutionIn a circle with centre O, chords AB and CD intersect inside the circumference at E. Prove that ∠AOC+ ∠BOD=2 ∠AEC
View SolutionIn a circle with centre O,chords AB and CD intersect inside the circumference at E.Prove that ∠AOC+∠BOD=2∠AEC
View SolutionTwo circle with centres A and B intersect at C and D. Prove that ∠ACB=∠ADB.
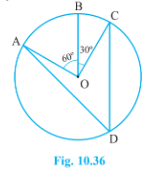
View SolutionIn Fig. 10.36, A,B and C are three points on a circle with centre O such that ∠BOC= 30o and ∠AOB= 60o. If D is a point on the circle other than the arc ABC, find ∠ADC.
View SolutionAB and CD are two parallel chords of a circle with centre O such that AB=6 cm and CD=12 cm. The chords are on the same side of the centre and the distance between them is 3 cm. The radius of the circle is 6 cm
View SolutionABCD is a parallelogram whose AC and BD intersect at O. A line through O intersects AB at P and DC at Q. Prove that ar ( POA)= ar ( QOC).
View SolutionIn Figure, it is given that AE=AD and BD=CE. Prove that AEB≅ADC
View SolutionABCD is a parallelogram whose diagonals AC and BD intersect at O. A Line through O intersects AB at P and DC at Q. Prove that ar(△POA)=ar(△QOC).
View SolutionIf AB is a chord of a circle, Pand Q are the two points on the circle different from A and B, then ∠APB= ∠AQB ∠APB+∠AQB=180∘ or∠APB= ∠AQB
View Solution
