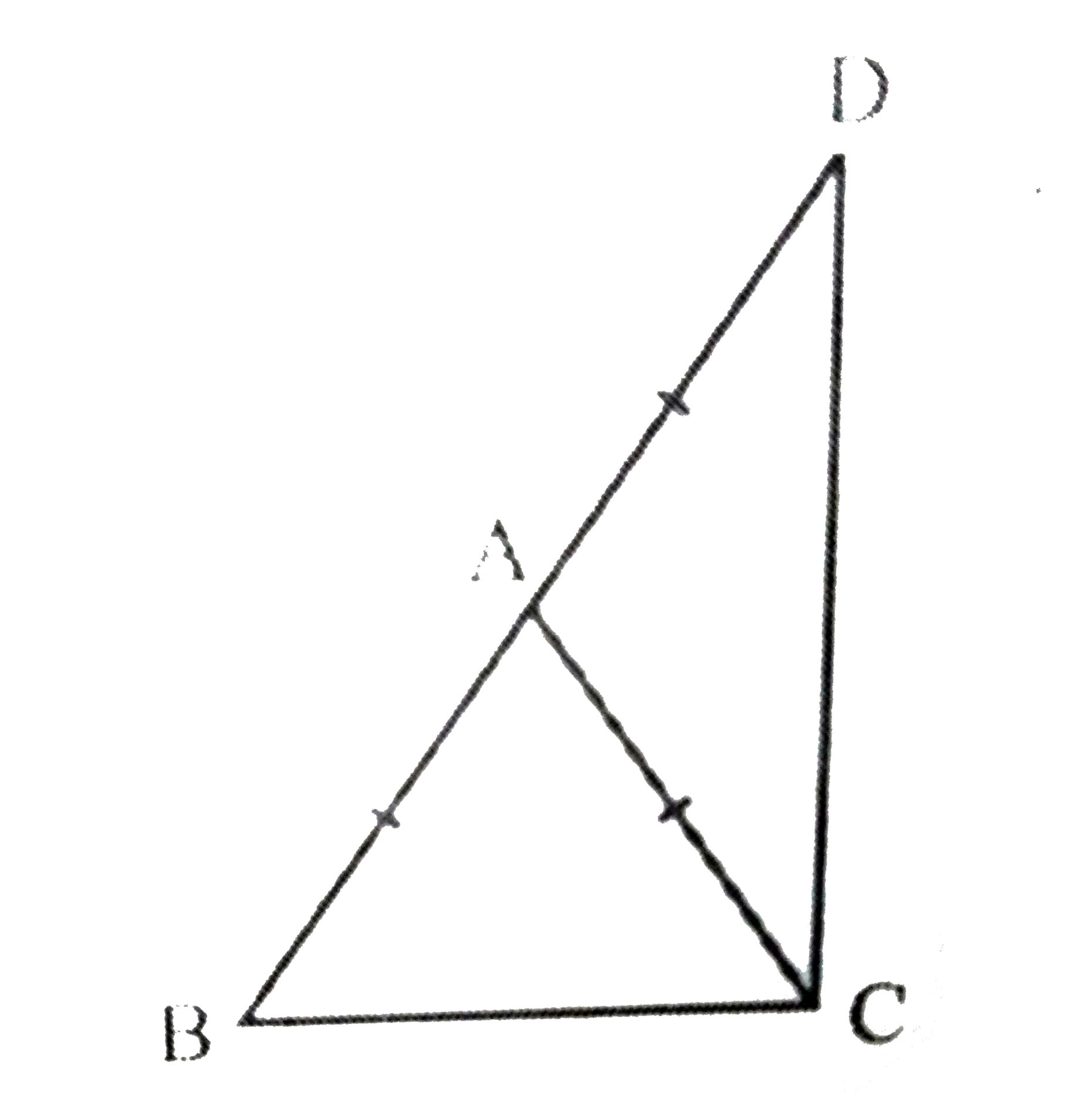
abc is an isosceles triangle with AB=AC. Side BAis produced to D such that AB=AD. Prove that ∠BCD is a right angle.
To prove that angle ∠BCD is a right angle in the given isosceles triangle ABC where AB=AC and AD=AB, we can follow these steps:
Step 1: Identify the Given Information
We know that:
- Triangle ABC is isosceles with AB=AC.
- Side BA is extended to point D such that AB=AD.
Step 2: Establish Relationships Between the Sides
From the given information, we have:
- AB=AC (1)
- AB=AD (2)
From (1) and (2), we can conclude that:
- AC=AD
Step 3: Analyze Angles in Triangle ABC
Since AB=AC, by the property of isosceles triangles, the angles opposite these equal sides are also equal:
- ∠ABC=∠ACB (3)
Step 4: Analyze Angles in Triangle ADC
In triangle ADC, since AC=AD, we can also say:
- ∠ADC=∠DCA (4)
Step 5: Set Up an Equation for the Angles
Now, we can add the angles from triangles ABC and ADC:
- From (3) and (4), we have:
∠ABC+∠ADC=∠ACB+∠DCA
Step 6: Substitute and Rearrange
Let’s denote:
- ∠ABC=x
- ∠ACB=x (from (3))
- ∠ADC=y
- ∠DCA=y (from (4))
Thus, we can write:
x+y=x+y
Step 7: Add ∠BCD to Both Sides
Now, we can add ∠BCD to both sides:
x+y+∠BCD=x+y+∠BCD
Step 8: Use the Triangle Sum Property
In triangle BCD, the sum of the angles is 180∘:
∠ABC+∠ADC+∠BCD=180∘
Substituting x+y into the equation gives:
x+y+∠BCD=180∘
Step 9: Solve for ∠BCD
Since x+y is equal to 180∘−∠BCD, we can rearrange this to find ∠BCD:
∠BCD=180∘−(x+y)
Step 10: Conclude that ∠BCD is a Right Angle
Since x+y represents the angles in triangle ABC and ADC, we conclude that:
∠BCD=90∘
Thus, we have proven that ∠BCD is a right angle.
---
We know that:
- Triangle ABC is isosceles with AB=AC.
- Side BA is extended to point D such that AB=AD.
From the given information, we have:
- AB=AC (1)
- AB=AD (2)
- AC=AD
Since AB=AC, by the property of isosceles triangles, the angles opposite these equal sides are also equal:
- ∠ABC=∠ACB (3)
In triangle ADC, since AC=AD, we can also say:
- ∠ADC=∠DCA (4)
Now, we can add the angles from triangles ABC and ADC:
- From (3) and (4), we have:
∠ABC+∠ADC=∠ACB+∠DCA
Let’s denote:
- ∠ABC=x
- ∠ACB=x (from (3))
- ∠ADC=y
- ∠DCA=y (from (4))
x+y=x+y
Now, we can add ∠BCD to both sides:
x+y+∠BCD=x+y+∠BCD
In triangle BCD, the sum of the angles is 180∘:
∠ABC+∠ADC+∠BCD=180∘
Substituting x+y into the equation gives:
x+y+∠BCD=180∘
Since x+y is equal to 180∘−∠BCD, we can rearrange this to find ∠BCD:
∠BCD=180∘−(x+y)
Since x+y represents the angles in triangle ABC and ADC, we conclude that:
∠BCD=90∘
Topper's Solved these Questions
Similar Questions
ΔABC is an isosceles triangle in which AB=AC. Side BA is produced to D such that AD=AB (see Fig. 7.34). Show that ∠BCD is a right angle.
 View Solution
View SolutionIn Figure, ABC is an isosceles triangle in which AB=AC.CPparel≤lAB and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA and (ii) ABCP is a parallelogram.
 View Solution
View SolutionIf ABC is an isosceles triangle such that AB=AC and AD is an altitude from A on BC . Prove that (i) ∠B=∠C (ii) AD bisects BC (iii) AD bisects ∠A
View SolutionABC is a triangle. D is a point on AB such that D=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC
View SolutionFill the blanks in the following so that each of the following statements is true.
(i) Sides opposite to equal angles of a triangle are ......
(ii) Angle opposite to equal sides of a triangle are .....
(iii) In an equilateral triangle all angles are .....
(iv) In a ΔABC if ∠A = ∠C , then AB = ......
(v) If altitudes CE and BF of a triangle ABC are equal, then AB = ....
(vi) In an isosceles triangle ABC with AB = AC, if BD and CE are its altitudes, then BD is …… CE.
(vii) In right triangles ABC and DEF, if hypotenuse AB = EF and side AC = DE, then ΔABC ≅ Δ ……View SolutionABC is a triangle. D is a point on AB such that AD=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC.
View SolutionIn Figure, BD and CE are two altitudes of a ABC such that BD=CE. Prove that ABC is isosceles.
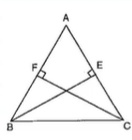 View Solution
View SolutionAny point D is taken in the base BC of a triangle ABC and AD is produced to E, making DE equal to AD. Show that ar (BCE)=ar(ABC)
View SolutionA triangle ABC is an isosceles triangle if any one of the following conditions hold: Altitude AD bisects ∠BAC. Bisector of ∠BAC is perpendicular to the base BC.
View SolutionIn figure, ABC is triangle in which ∠ABC=90∘and AD⊥CBproduced. Prove that AC2=AB2+BC2−2BC.BD.
 View Solution
View Solution

