In Figure, are respectively the bisectors of and . Prove that
To prove that triangle EBC≅FCB, we will follow these steps:
Step 1: Identify Given Information
We are given:
- AB=AC (Sides of triangle ABC are equal)
- BE and CF are the angle bisectors of ∠B and ∠C respectively.
Step 2: Establish Equal Angles
Since AB=AC, by the property of isosceles triangles, we know that:
∠ABC=∠ACB
Let’s denote these angles as x. Therefore, we have:
∠ABC=xand∠ACB=x
Step 3: Use the Angle Bisector Property
Since BE is the angle bisector of ∠B, we have:
∠EBC=12∠ABC=x2
Similarly, since CF is the angle bisector of ∠C:
∠FCB=12∠ACB=x2
Step 4: Establish Common Sides
In triangles EBC and FCB, we have:
- BC is a common side.
Step 5: Establish Corresponding Angles
From the previous steps, we have:
∠EBC=∠FCB=x2
Also, we know:
∠ECB=∠EBC(as established)
Step 6: Apply the ASA Criterion
Now we have:
- ∠EBC=∠FCB
- BC is common
- ∠ECB=∠EBC
Thus, by the Angle-Side-Angle (ASA) criterion, we can conclude that:
△EBC≅△FCB
Conclusion
Therefore, we have proved that △EBC≅△FCB.
---
We are given:
- AB=AC (Sides of triangle ABC are equal)
- BE and CF are the angle bisectors of ∠B and ∠C respectively.
Since AB=AC, by the property of isosceles triangles, we know that:
∠ABC=∠ACB
Let’s denote these angles as x. Therefore, we have:
∠ABC=xand∠ACB=x
Since BE is the angle bisector of ∠B, we have:
∠EBC=12∠ABC=x2
Similarly, since CF is the angle bisector of ∠C:
∠FCB=12∠ACB=x2
In triangles EBC and FCB, we have:
- BC is a common side.
From the previous steps, we have:
∠EBC=∠FCB=x2
Also, we know:
∠ECB=∠EBC(as established)
Now we have:
- ∠EBC=∠FCB
- BC is common
- ∠ECB=∠EBC
△EBC≅△FCB
Therefore, we have proved that △EBC≅△FCB.
Topper's Solved these Questions
Similar Questions
In Fig. 4.102 (i) and (ii) , if CD and GH (D and H lie on AB and FE ) are respectively bisectors of ∠ACB and ∠EGF and ABC~FEG , prove that (FIGURE) DCA~HGF (ii) CDGH=ACFG (iii) DCB~HGE
View SolutionIn figure AB=AC and CP∣∣BA and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA (ii) ABCP is a parallelogram
View SolutionIn ABC, D, E and F are, respectively, the mid-points of BC, CA and AB . If the lengths of side AB, BC and CA are 7cm, 8cm, and 9cm, respectively, find the perimeter of DEF
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ

View SolutionIn Figure, ABCD and AEFG are two parallelograms. If ∠C=580, find ∠F
View SolutionIn Fig. 4.103, CD and GH are respectively the medians of ABC and EFG . If ABC~FEG , prove that (FIGURE) ADC~FHG (ii) CDGH=ABFE (iii) CDB~GHE
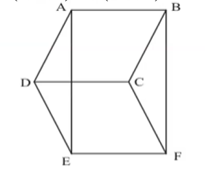
View SolutionIn Figure, ABCD, ABFE and CDEF are parallelograms. Prove that ar(ADE)=ar(BCF)
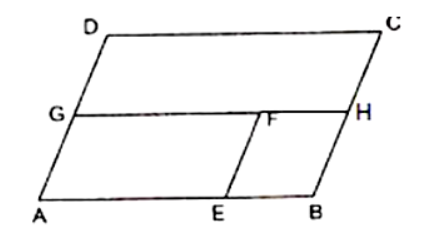
View SolutionIn Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE trisect (divide into three equal parts) the diagonal BD .
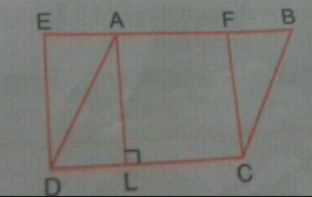
View SolutionIn the following figure, ABCD is a parallelogram and EFCD is a rectangle. Also, AL⊥DC. Prove that
(i) ar(ABCD)=ar(EFCD)
(ii) ar(ABCD)=DC×AL.
View SolutionIn Fig. 71, if ABCD and CDEF, find ∠ACE
View Solution
