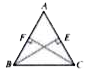
If the altitudes from two
vertices of a triangle to the opposite sides are equal, prove that the
triangle is isosceles.
In△ABEand △ACF∠AEB=∠AFC(900each)
∠BAE=∠CAF(common angle)
∠ABE=∠ACF using angle sum property
BE=CF,△ABE≅△ACF
⇒AB=AC
Hence triangle ABC is an isosceles tangent as two sides are equal to each other
Video Solution
Text Solution
In△ABEand △ACF,∠AEB=∠AFC(900each)
∠BAE=∠CAF(common angle)
∠ABE=∠ACFusing angle sum property
BE=CF,△ABE≅△ACF
⇒AB=AC
Hence triangle ABC is an isosceles tangent as two sides are equal to each other
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If △ABC is an isosceles triangle with ∠c=90∘ and AC = 5 cm then AB is:
A5 cmB2.5 cmC10 cmD5√2cmIf ABC is an isosceles triangle with ∠C=90∘ and AC=5 cm, then AB is:
A5 cmB10 cmC5√2cmD2.5 cmIn △ABC ,AB=AC , ∠B=40∘ Then ∠C is equal to
A50∘B40∘C80∘D140∘
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
View SolutionShow that in an isosceles triangle, angles opposite to equal sides are equal.
View SolutionShow that in an isosceles triangle, the angles opposite to the equal sides are equal.
View SolutionABC is a triangle and D is the mid-point of BC . The perpendiculars from D to AB and AC are equal. Prove that the triangle is isosceles.
View SolutionIf the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
View Solution