If is an isosceles triangle such that and is an altitude from on . Prove that (i) (ii) bisects (iii) bisects
(given)
(common)
.
Topper's Solved these Questions
Similar Questions
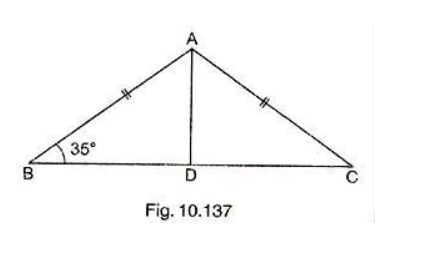
ABC is an isosceles triangle such that AB=ACandAD is the median to base BC . Then, ∠BAD=
(a) 55∘
(b) 70∘
(c) 35∘
(d) 110∘
View SolutionIn Figure, ABC is an isosceles triangle in which AB=AC.CPparel≤lAB and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA and (ii) ABCP is a parallelogram.

View Solution
Knowledge Check
In an isosceles triangle ΔABC,AB=AC and ∠A=80∘. The bisector of ∠Band∠C meet at D. The ∠BDC is equal to the
A90∘B100∘C130∘D80∘
In an isosceles triangle ABC, with AB=AC, the bisectors of B and C intersect each other at O. Join A to O. Show that :
(i) OB=OC
(ii) AO bisects A
View SolutionABC is an isosceles triangle in which AB=AC. AD bisects exterior angle PAC and CD∣∣AB. Show that(i) ∠DAC=∠BCA and (ii) ABCD is a parallelogram.
View SolutionIn an isosceles triangle ABC , if AB=AC=25cm and BC=14cm , then the measure of altitude from A on BC is (a) 20cm (b) 22cm (c) 18cm (d) 24cm
View SolutionIn ABC,∠A=900andAD is an altitude. Complete the relation BDDA=AB() .
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that AP bisects \ ∠A as well as ∠D AP is the perpendicular bisector of BC
View SolutionIn Fig. 4.124, E is a point on side CB produced of an isosceles triangle ABC with AB=AC . If AD⊥BC and EF⊥AC , prove that (i) ABDECF (ii) AB×EF=AD×EC . (FIGURE)
View SolutionLet ABC be an isosceles triangle with AB=AC and let D, E, F be the mid points of BC, CA and AB respectively. Show that AD⊥FE and AD is bisected by FE
View Solution